超导重力观测噪声水平的极大似然估计*
2011-09-20韦进李辉刘子维康开轩
韦进 李辉 刘子维 康开轩
1)武汉大学测绘学院,武汉4300792)中国地震局地震研究所,武汉4300713)地壳运动与地球观测实验室,武汉430071
超导重力观测噪声水平的极大似然估计*
韦进1,2,3)李辉2,3)刘子维2,3)康开轩2,3)
1)武汉大学测绘学院,武汉430079
2)中国地震局地震研究所,武汉430071
3)地壳运动与地球观测实验室,武汉430071
利用极大似然估计和3种互不相关的噪声(白噪声,闪烁噪声,游走噪声)模型及其组合,对SG-053超导重力仪产出的重力固体潮整时值残差时间序列进行分析,得出残差时间序列中明显存在彩色噪声(闪烁噪声、游走噪声):白噪声1.40×10-8ms-2,闪烁噪声1.85×10-8ms-2,游走噪声为2.40×10-8ms-2。该方法估计的白噪声水平与潮汐分析方法得出的结果一致。
超导重力仪;残差时间序列;极大似然估计;噪声水平;白噪声
AbstractThe instrument noise level is one of the most important factor for the evaluation of SG-053.The tidal gravity residual time series of the SG-053 has been analyised with maximum likelihood estimation(MLE)and three noise(white noise,flicker noise,walk noise)models and their combination.It is shown that there is color noise in the tidal gravity residual,the white noise level is 1.40×10-8ms-2,the flicker noise 1.85×10-8ms-2and the random walk noise 2.40×10-8ms-2.This analysis result is consistent with the tidal analysis.
Key words:superconducting gravimeter;residual time series;maximum likelihood estimation;noise level;white noise
1 引言
超导重力仪的噪声水平的量级是仪器性能的重要指标,它是选择台址[1],影响潮汐分析的重要因素[2,3]。文献[3,4]1997年利用武汉基准站超导重力仪确定了一种所谓的“单边”噪声,据经验估计量级在(0.2~0.8)×10-8ms-2。目前,分析超导重力仪噪声水平的主要方法是潮汐分析[1]。用两套潮汐分析软件(VAV与ETERNA)可以估计仪器的白噪声。文献[2]在利用超导重力仪精密测定地球潮汐常数时,认为武汉台站背景噪声较大,约为1.5× 10-8ms-2。而在很多地球物理现象中,时间序列噪声可以被描述成为一个幂率过程[5]。在连续GPS观测中采用幂率噪声模型来估计测站位移速率,能够很好地减少由于幂率噪声影响的低频振幅的影响[7-11]。实际上利用超导重力仪观测数据进行分析时,同样需要进行复杂的数据处理(滤波、潮汐分析、潮汐改正、气压改正等)。而这样的过程可能会引入和连续GPS分析类似的噪声。因此,如果对残差时间序列依然采用白噪声模型进行估计,也可能引入幂率(彩色)噪声,进而可能影响仪器性能的判定和台址选择。
本文利用潮汐模型、气压观测时间序列改正后的重力固体潮后的残差时间序列研究超导重力仪白噪声和幂率(彩色)噪声之间的规律,并利用极大似然估计方法估计各噪声分量的噪声水平。
2 噪声数据的极大似然估计
2.1 极大似然估计
MLE(极大似然估计)[10]可以用于计算时间序列中白噪声和幂率(彩色)噪声的量级。在考虑幂率过程时,MLE可根据不同幂率(彩色)噪声模型来估计对应模型的噪声量级。用MLE估计噪声项时,平差数据的协因数阵具最大的概率密度。概率密度方程为:
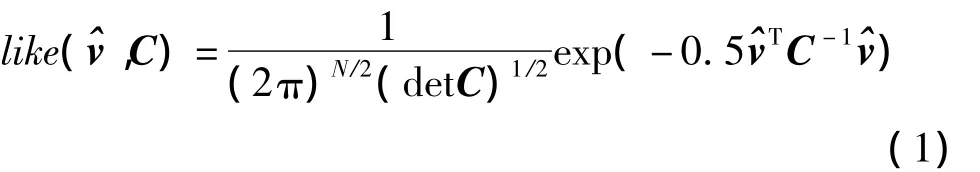
式中,like是极大似然值,det是矩阵的行列式。两边取自然对数:
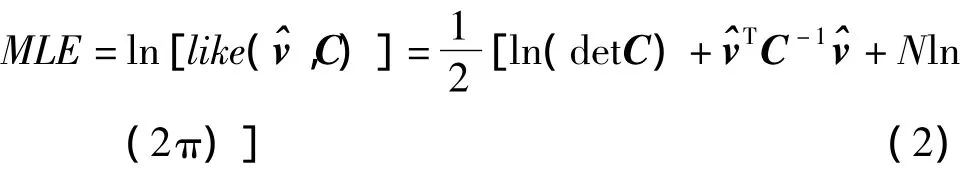
这里ln是自然对数,N是采样数,C是数据的协因数,v是利用C协因数和加权最小二乘对原始数据估计出来的残差。
利用极大似然估计的方法对扣除实际模型的理论固体潮值和气压影响后的残差进行白噪声分析的模型如下:
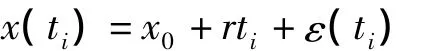
式中,x(ti)是经过潮汐和气压改正后的残差,x0是重力的常数项,r是重力仪的漂移。考虑到残差中也存在周期信号,则可写为:


当ε(ti)=aαj(t)+bβj(t)时,利用极大似然估计,残差的协因数为Cx=a2I+b2Jκ。
2.2 模型定义
白噪声模型认为观测数据之间没有相关性。而其他幂率(彩色)噪声模型通过不同的表达方式反映了观测数据之间存在相互关系[11]。各模型协因数阵C、噪声水平a、b和中误差σ如下:
1)白噪声模型:b=0,Cx=a2I,C-1x=(1/a2)I
2)闪烁噪声模型:a=0,Cx=b2Jκ,C-1x=(1/

这里,N为采样数,T为时间跨度[13]。
4)白噪声加闪烁噪声:a≠0,b≠0,Cx=a2I+ b2Jκ,κ=1。
5)白噪声、游走噪声和闪烁噪声:a≠0,b≠0,Cx=a2I+b2J1+c2J2。
复合噪声模型用Brent[14]算法实现参数估计。
3 数据处理计算与结果分析
3.1 残差时间序列
用国际固体潮中心[15]提供的VAV(V03.11)和ETERNA34潮汐分析软件对SG-053超导重力仪2009-03-01—09-01预处理后的整时值和气压观测数据联合进行潮汐分析。除了分析各潮波的潮汐因子和相位外,还分析了残差的振幅中误差和气压导纳值(表1)。

表1 VAV和ETERNA的潮汐分析白噪声分析结果Tab.1Tidal analysis results of the VAV and ETERNA
VAV与ETERNA软件均采用最小二乘方法估计潮汐参数。但在漂移模型、气压回归因子和扰动数据剔除等方面各自采用了不同的方法消除系统误差和粗差对参数估计的影响[1]。从上述分析结果来看两套软件计算的气压导纳值之间和白噪声水平之间趋于同一量级。气压导纳值在(-0.322 29~-0.302 361)×10-8ms-2/hPa之间,白噪声水平在(1.1~1.4)×10-8ms-2水平范围内。而且从图1可以看到,利用两个模型的残差序列的差不超过0.004×10-8ms-2的量级,表明利用两个潮汐模型和气压导纳值模型改正后的序列几乎是相同的。
对重力固体潮进行潮汐改正和气压改正后的残差时间序列以及它们之间的差值见图1。
3.2 不同模型的极大似然估计
和潮汐分析方法不同,极大似然估计在已知估计参数的数学期望的情况下,能够无偏地估计出系统误差中和时间相关的误差影响[6-8]。然而,仪器在观测过程中不可避免地受到外界因素的干扰,出现直接影响估计结果的粗差。因此,在已知时间序列变化速率、各波群振幅相位的数学期望值的前提下,利用极大似然估计选择最优的估计参数,从而无偏地估计出不同噪声模型的噪声水平。
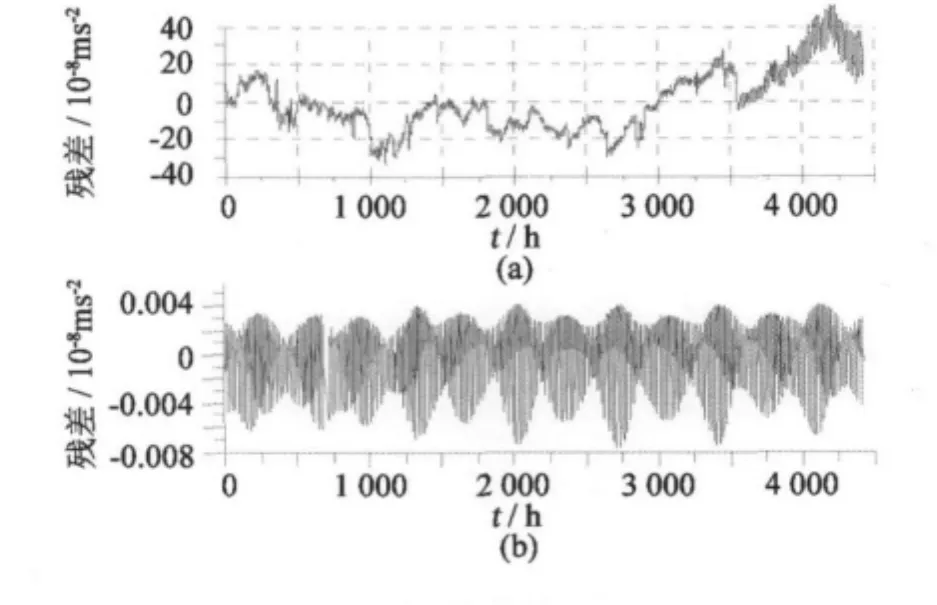
图1 SG-053超导重力仪2009-03-01—09-01残差时间序列(a)和两个模型残差的差结果(b)Fig.1Residual time serial of SG-053 between 2009-03-01 and 2009-09-01(a)and difference between the results of two model residuals(b)
3.2.1 模型分波频率的关系
利用残差时间序列和5种噪声模型进行极大似然估计。计算出从起始的2 000小时观测数据不同周期下各模型的噪声水平、极大似然值之间的关系(表2)。
进行极大似然估计,在利用6个周期时,各模型均出现了极大值拐点现象;超过7个周期后,模型全部出现系统粗差现象;但采用不同的周期对极大值及其噪声分量的估计影响不大。同时,组合模型的估计明显优于单一模型的估计(极大值普遍较大),组合模型估计出的各噪声分量在数量级上基本一致(白噪声水平在(1.6~1.8)×10-8ms-2,闪烁噪声在(2.1~2.8)×10-8ms-2)。而且利用3种模型的估计极值优于其他各模型。分析表明,利用6周期和复合噪声模型的估计能更加有效地估计出观测时间序列的各噪声水平。
3.2.2 模型采样数和采样时段的关系
根据残差时间序列,利用3种噪声的组合模型进行极大似然估计。计算周期数为6的情况下,两个组合模型、采样数和采样时段的关系如图2所示。
1)模型和采样数的关系
图2(a,b)是利用两种组合噪声模型,以残差时间序列的起点作为起点,估计出的各模型的噪声分量和观测数据长度之间的关系。在采样数为1 500~3 000的各噪声水平均趋于平稳(变化不超过0.5 ×10-8ms-2)。而当采样数在800~1 000时范围内时,3类噪声水平普遍不稳定,其主要原因是采样数不够。观测采样数超过该范围到3 500时,各模型的噪声水平开始同步上扬,其主要原因是后期的观测数据出现了不明原因的噪声(图1)。
2)模型和采样时段的关系
图2(c,d)是利用两种组合噪声模型,以100为滑动步长取不同的滑动起点,估计出的各组合模型的各噪声分量和采样时段之间的关系。而每个点是不同观测数据长度下极大估值的个噪声分量的均值和方差。该时间序列表明:两个组合模型的各噪声分量都表现出先减小后增大的过程,各噪声分量的变化也一致。在1 300小时作为起点估计的各噪声分量达到了极小值。
3)模型、采样数和采样时段之间的关系
从模型、采样数和采样时段之间的关系表明,无论是WN+FN+RWN还是WN+FN模型,利用极大似然估计后,它们都表现出了在1 300小时为起始点,1 000~1 500小时窗口达到各噪声分量的极小值。但是两个组合模型估计出的图3描述了两个组合模型的白噪声分量、采样数量和采样时段之间的关系。
3.2.3 组合模型的极大似然估计
分析表明,利用组合模型和最优估计参数(分波周期、组合模型、采样数量和采样时段)采用Brent algorithm算法[12]实现了两种组合模型的各噪声水平分量的估计(图4)。分析结果表明在横坐标为53°,纵坐标为46°时达到极大值:白噪声水平为1.40×10-8ms-2,闪烁噪声水平为1.85×10-8ms-2,游走噪声为2.40×10-8ms-2。该分析结果中白噪声的分量与潮汐分析的结果一致。
4 结论与讨论
1)利用SG-053预处理后的4 422个采样数据进行潮汐分析和进行了潮汐改正和气压改正后的残差序列进行极大似然估计结果表明,两个软件分析的残差序列相差不超过0.004×10-8ms-2;白噪声量级趋于一致,在(1.1~1.4)×10-8ms-2范围内。
2)在最优的分析参数下,利用Brent算法计算两组合模型的各噪声分量,结果都趋于一致。但是用WN+FN+RWN估计出的当前重力固体潮残差时间序列的噪声量级为:白噪声水平为1.40×10-8ms-2,闪烁噪声水平为1.85×10-8ms-2,游走噪声为2.40×10-8ms-2。这一分析结果中白噪声的分量和潮汐分析的分析结果趋于一致。
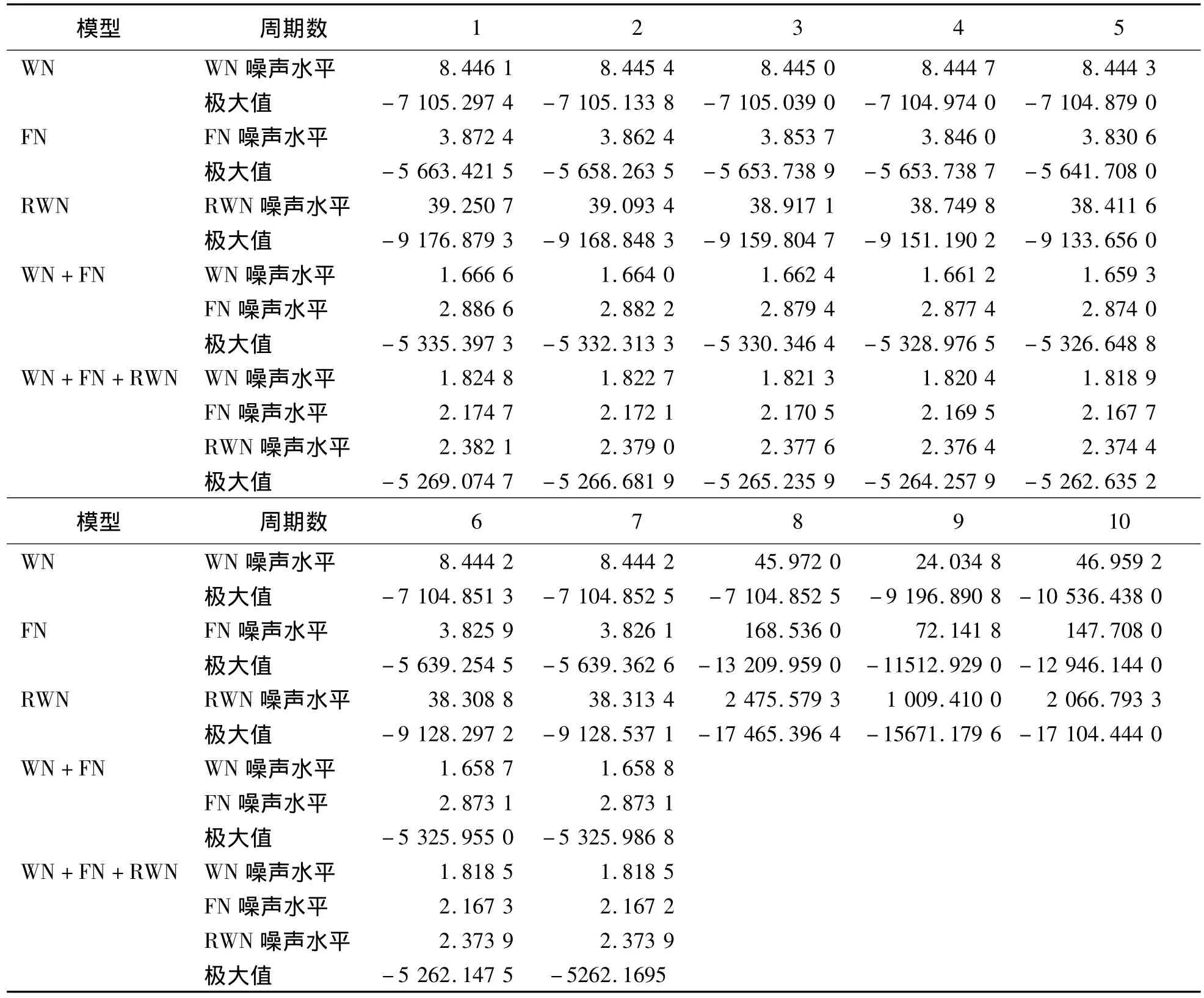
表2 周期、数噪声水平和极大值之间的关系Tab.2Relations among period,noise level and maximum value

图2 两种组合模型采样数和各噪声水平关系序列Fig.2Relation between sample numbers and the noise level with the two types of combined model
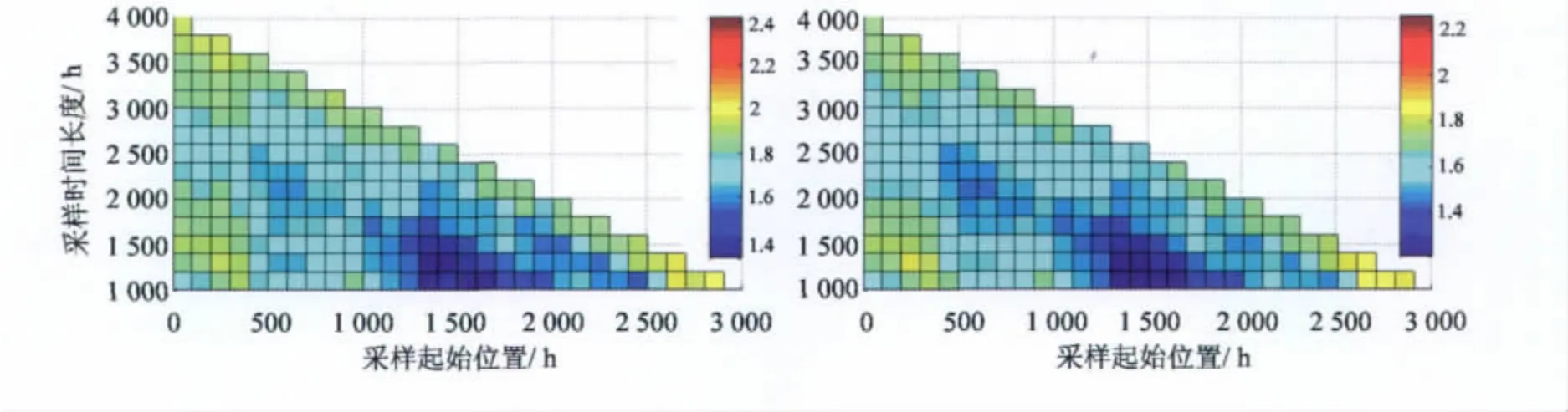
图3 组合模型采样数和采样时段之间的关系Fig.3Relations between sample numbers and sample period with the two types of combined model

图4 Brent算法的极大似然估计Fig.4Brent maximum likelihood estimation algorithm
1田桂娥,等.VAV和ETERNA潮汐分析方法的比较和研究[J].大地测量与地球动力学,2009,(2):96-99.(Tian Guie,et al.Comparison and investigation of VAV and ETERNA tidal analysis methods[J].Journal of Geodesy and Geodynamics,2009,(2):96-99)
2孙和平,等.用超导重力仪观测数据精度测定地球潮汐常数[J].地壳形变与地震,1997,(4):17-25.(Sun Heping,et al.The constant precision determination of the earth tides with superconducting gravimeter datums[J].Crustal Deformation and Earthquake,1997,(4):17-25)
3徐建桥.重力固体潮汐理论及分析方法——武昌台超导重力仪观测资料的分析处理[D].中国科学院测量与地球物理研究所,1997.(Xu Jianqiao.The theory and analysis of gravity tidal——superconducting gravimeter data analysis and processing in Wuchang station[D].Institute of Geodesy and Geophysics Chinese Academy of Sciences,1997)
4Kroner C,et al.Long-term stability and tidal parameters of the SCG-record at Wuhan[A].Proceedings 12th International Symposium on Earth Tides[C].1995:265-276.
5Mandelbrot B and Van Ness J.Fractional brownian motions,fractional noises,and applications[R].SIAM Rev.1968,10,422-439.
6Simon D and Williams P.Error analysis of continuous GPS position time series[J].Journal of Geophysical Research,2004,109(B03412):19.
7Simon D and Williams P.The effect of coloured noise on the uncertainties of rates estimated from geodetic time series[J].Journal of Geodesy,2003,76:483-494.
8John Langbein.Correlated errors in geodetic time series:Implications for time-dependent deformation[J].Journal of Geophysical Research,1997,102(B1):591-603.
9Ailin Mao,et al.Noise in GPS corrdinate time series[J].Journal of Geophysical Research,1999,104(B2):2 797-2 816.
10Simon D and Williams P.CATS:GPS coordinate time series analysis software[J].GPS solut,2008,12:147-153.
11Jie Zhang,et al.Southern California permanent GPS geodetic array:error analysis of daily position estimates and site velocities[J].Journal of Geophysical Research,2007,102: 18 035-18 055.
12Teferle F N,et al.Crustal motions in Great Britain:evidence from continuous GPS,absolute gravity and Holocene sea level data[J].Geophy.J.Int.,2009,178:23-46.
13Johnson H O and Wyatt FK.Geodetic network design for fault-mechanics studies[J].Manuscr.Geod.,1994,(10): 309-323.
14Press WH,et al.Numerical recipes[M].New York:Cambridge University Press,2007.
15Jean-Pierre.ETERNA[EB/OL].http://www.observatoire.be/ICET/soft/index.html, 2010-07-01/2010-12-15.
NOISE LEVEL MEASUREMENT OF SG-053 WITH MLE
Wei Jin1,2,3),Li Hui2,3),Liu Ziwei2,3)and Kang Kaixuan2,3)
1)School of Geodesy and Geometics,Wuhan University,Wuhan430079
2)Institute of Seismology,CEA,Wuhan430071
3)Crustal Movement Laboratory,Wuhan430071
P207;P203
A
1671-5942(2011)03-0069-06
2010-12-25
国家自然科学基金(41004030);中国地震局地震研究所所长基金(IS200951041)
韦进,男,1981年生,博士研究生,助理研究员,主要从事重力台网管理和重力固体潮分析研究.E-mail:pierce212@163.com
