铝泡沫复合材料夹芯梁的弯曲性能

周广涛，王新筑

(1.华侨大学 机电及自动化学院，厦门 361021;2.重庆大学 a.工程力学系力学博士后流动站，b.煤炭灾害动力学与控制国家重点实验室，重庆 400044)

金属泡沫材料是20世纪80年代后期国际上迅速发展起来的一种物理功能与结构一体化的新型工程材料，多孔结构和金属特征使其得以具备其他实芯材料未有的功能，如防震、吸声、屏蔽、质轻及结构功能一体化等突出特点。其中最有前途的应用是作为轻－硬夹芯结构的芯子，使得金属泡沫夹芯结构在具有低密度的同时兼有良好的抗剪切和断裂强度。金属泡沫夹芯结构比目前广泛使用的蜂窝夹芯结构具有一系列突出特点，如在温度超过300°时力学性能仍能保持稳定，抗腐蚀性强，能加工成复杂形状等［1－2］，一度成为研究的重点。弯曲载荷是夹芯结构在工程应用中受到的主要载荷形式，因此在力学性能的研究上，弯曲载荷是该材料研究的主要领域。何德坪等［3－5］根据球形孔铝泡沫合金和铝泡沫夹芯梁的三点弯曲载荷－位移曲线，研究了4种常见破坏模式，并建立了破坏模式图。虞吉林等［6］利用霍普金森装置研究了开孔金属泡沫芯子铝面板夹芯结构在静载和动载弯曲作用下的失效机制。Gibson等［7－9］研究了三点弯曲载荷作用下的金属面板铝泡沫夹芯结构分别在常温和高温下的失效模式和蠕变行为，得到了失效载荷图。Fleck等［10］从理论和试验上研究了不同边界条件下的铝面板铝合金泡沫芯子夹芯结构在三点弯曲载荷作用下的失效机制，并绘制了失效机制图。还有其他一些学者对完好和面板含缺陷的金属面板金属泡沫夹芯结构在四点弯曲载荷下的破坏模式、失效机制及承载能力进行了研究［11－15］。

目前，国内外学者研究的金属泡沫夹芯结构其面板多为金属面板，金属泡沫复合材料面板要比金属泡沫金属面板夹芯结构具有更明显的优势。因此，本文自行设计和制造了金属泡沫复合材料夹芯结构，并对该结构的弯曲力学性能进行了研究，具有一定的理论意义。

1 材料制备

本文所设计的金属泡沫复合材料夹芯结构的面板为高强玻璃纤维/环氧树脂(S2/TDE－85，固化剂为70#酸酐)层合板。它由单层预浸料按一定铺层角度(45/－45/0/－45/45)手糊铺设而成，通常00单层用来承受轴向载荷，±450单层用来承受剪切载荷。单层预浸料厚度0.2 mm，纤维体积含量54%，固化度97%。芯子为闭孔铝泡沫，厚度为10 mm，相对密度0.15，平均孔径为2 mm左右。单层预浸料和铝泡沫芯子的力学性能参数见表1。

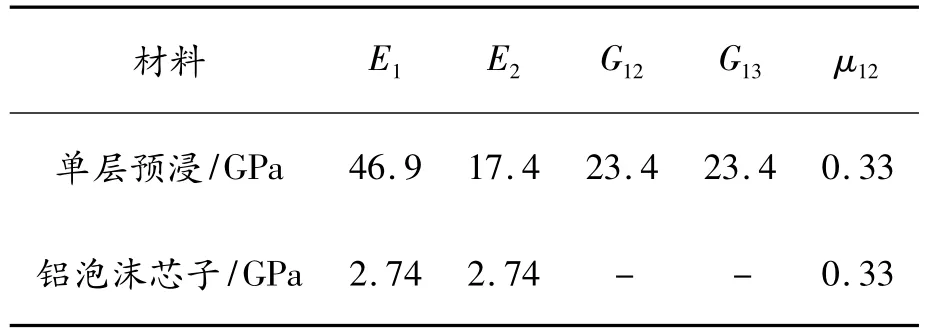
表1 单层预浸料和铝泡沫芯子的力学性能参数

复合材料层合面板和铝泡沫芯子采用二次固化方法粘接在一起。具体步骤:将常温下的胶膜放置在金属泡沫上;然后将固化后并按试样尺寸加工的面板置于胶膜之上，将其放置在热压机上，加温加压，并保持1 h;最后将其取出，常温下冷却即成金属泡沫夹芯结构。胶膜采用J47A，其属于中温固化结构胶，可产生较小的翘曲变形和内应力，产品外形精度较高，广泛用于复合材料二次成型。

2 弯曲试验

三点弯曲性能实验参照ASTM C393－06标准［16］进行。试件尺寸为200 mm×60 mm×12.2 mm，每组5个试件。试验温度23%，湿度56%，所有试验均在INSTRON5569型万能电子试验机上进行。外伸梁的跨距L为160 mm。加载压头为高强度钢平压头，压头宽度15 mm。采用位移控制加载，加载速率为2 mm/min，连续加载，计算机自动记录弯曲载荷和弯曲位移，并绘制载荷－位移曲线。采用奥林巴斯显微镜(SZ-STU2)观察试件破坏模式。为了减少压头和试件之间摩擦，在加载压头与试件之间垫上一块硬质橡胶垫片，其宽度大于压头宽度，厚度为3 mm。

图1和图2分别为芯子厚度10 mm的夹芯结构试件破坏的显微镜照片和P－δ响应曲线。

3 分析和讨论

3.1 失效模式和曲线分析

由图1可知，芯子厚度为10 mm的弯曲试件失效模式为面板皱曲。铝泡沫复合材料夹芯结构的P－δ曲线可分为3个阶段(图2)，即线弹性段、弹塑性段和破坏后的失稳段。在线弹性段，夹芯结构发生线弹性弯曲变形，卸载后变形可以恢复;位移继续增加，面板内部的薄弱位置达到屈服应力，夹芯梁发生不可恢复的塑性变形，载荷增加的速度变缓。极限载荷以后的失稳段是由于夹芯梁的面板发生皱曲，此时梁的承载能力开始明显下降。

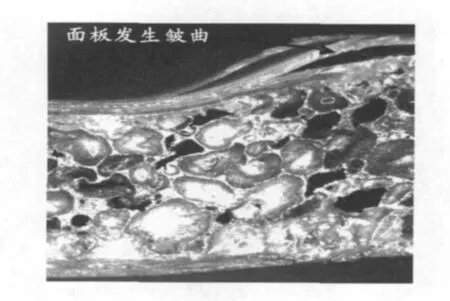
图1 弯曲夹芯结构试件的破坏微观照片

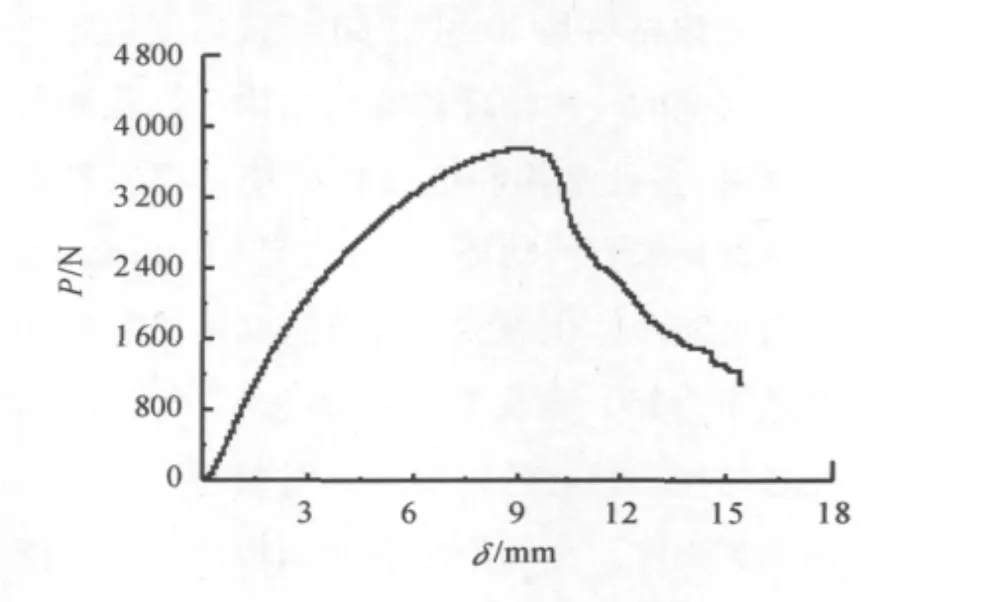
图2 弯曲夹芯结构试件的的P－δ曲线

3.2 抗弯刚度

图3为一典型的夹芯梁示意图，梁中点作用一载荷P，两端简支，跨距L。用下角标f和c分别表示面板和芯子，面板厚为tf，芯子厚度为tc，夹芯梁上、下面板形心之间的距离d=tc+tf，夹芯梁宽为b。Ef为面板弹性模量，Ec和Gc分别为芯子弹性模量和剪切模量。

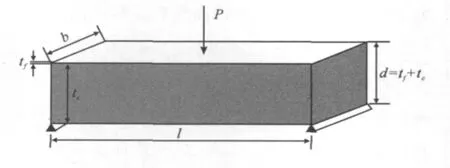
图3 夹芯梁

梁的抗弯刚度又称为弯曲刚度，用EI来表示，E为弹性模量，I是面积的二次矩。可用P/δ描述铝泡沫复合材料夹芯结构的弯曲刚度。P/δ曲线初始直线段的斜率表示夹芯梁的加载刚度。1969年，Allen［17］给出了夹芯梁在三点弯曲载荷下中点挠度δ的计算公式，即

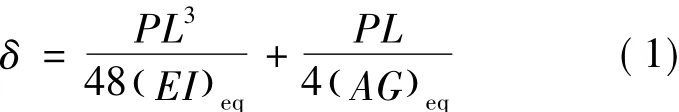
其中:(EI)eq为等效抗弯刚度;(AG)eq为等效剪切刚度。

如果 Ec≤Ef、tf≤tc，则(EI)eq和(AG)eq分别为

式中Gc为芯子的剪切模量。

将已知各参数代入式(2)，可得到加载刚度理论值。试验的平均值与理论值见表2。

表2 铝泡沫夹芯梁的弯曲刚度理论结果与试验值对比

由表2可知，试验结果大于理论值，这可能是理论公式中没有考虑胶层对刚度的贡献，而且对于芯子为多孔材料的夹芯结构，面板和芯子粘接时，结构胶会渗入与面板相邻的泡沫孔中形成胶钉，其对刚度也有所贡献。

3.3 比刚度

文献［18］指出，一般可用比刚度E1/2/ρ来综合评价夹芯结构的抗弯特性。其中E为夹芯结构的弯曲弹性模量，ρ为夹芯结构的密度。金属泡沫夹芯结构的等效弯曲弹性模量为

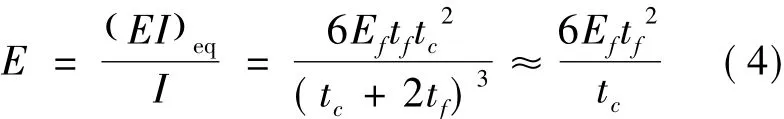
把求解结果和文献［16］中的3种金属泡沫夹芯结构进行了对比，结果见表3所示。

由表3可见，与其他3种常见金属泡沫夹芯结构的弯曲比刚度相比，本文所设计的金属泡沫复合材料夹芯结构具有较高的弯曲比刚度和明显的重量优势，而且复合材料面板具有良好的可设计性，通过对其优化设计，可以提高夹芯结构的比刚度。

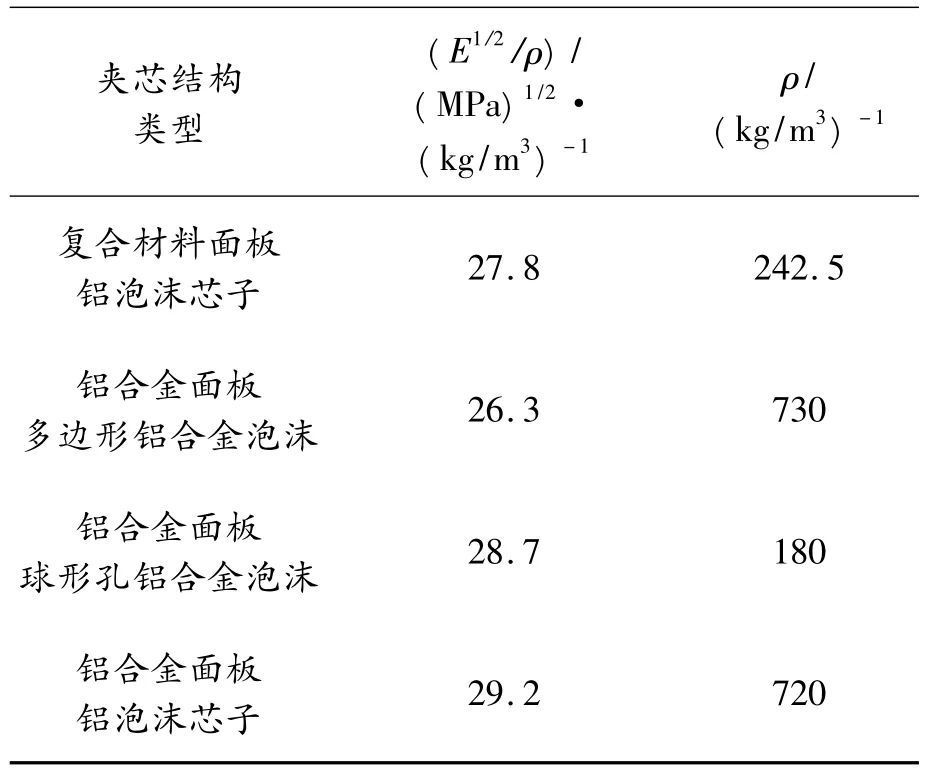
表3 几种金属泡沫夹芯结构的比刚度

3.4 失效模式和失效载荷的验证

将已知各参数带入文献［18］各失效模式对应的方程中，可得到各种失效模式下对应的失效载荷，其中最小的失效载荷即为本文所研究的夹芯结构发生失效时的最小载荷值，其对应的失效模式即为该结构的失效形式。铝泡沫复合材料夹芯梁的尺寸及极限载荷如表4所示。

表4 铝泡沫夹芯梁的几何尺寸和极限载荷

由表4可知，在给定几何参数tf、tc和L以后，铝泡沫夹芯梁的预测破坏模式与实际破坏模式符合较好，极限载荷理论值高于试验值，主要原因如下:理论求解是在假设夹芯结构完好的基础上进行的，但实际上由于制备和加工原因，铝泡沫夹芯结构内部肯定存在损伤，会使夹芯结构整体性能略有下降。

4 结束语

本文所设计的铝泡沫复合材料夹芯结构在三点弯曲载荷作用下的失效模式为面板层间脱层。铝泡沫复合材料夹芯结构的弯曲刚度理论预报值与试验值吻合较好。与其他3种常见的金属泡沫芯子金属面板夹芯结构相比，本文所设计的金属泡沫复合材料夹芯结构具有较高的弯曲比刚度和明显的重量优势及可设计性。铝泡沫复合材料夹芯梁的预测破坏模式与实际破坏模式符合较好，极限载荷理论值高于试验值。

［1］Dirk Schwingela，Hans-Wolfgang Seeligera，Claude Vecchionaccib，et al.Aluminium foam sandwich structures for space applications［J］.Acta Astronautica，2007，61:326－330.

［2］John Banhart，Seeliger H W.Aluminium Foam Sandwich Panels:Manufacture，Metallurgy and Applications［J］.Advanced Engineering Materials，2008，10:793 －802.

［3］张林，何德坪.球形孔泡沫铝合金三明治梁的三点弯曲变形［J］.材料研究学报，2005，19(4):361 －368.

［4］赵龙，何德坪，单键.高比强高孔隙率泡沫铝合金三明治梁［J］.材料研究学报，2004，18(5):485 －493.

［5］尚金堂，何德坪.泡沫层合梁的三点弯曲变形［J］.材料研究学报，2003，17(1):31 －38.

［6］Yu J L，Wang X，Wei Z G，et al.Deformation and failure mechanism of dynamically loaded sandwich beams with aluminum foam core［J］.International Journal of Impact Engineering，2003，28:331 －347.

［7］McCormack T M，Miller R，Kesler O，et al.Failure of sandwich beams with metallic foam cores［J］.Solids and Structures，2001，38:4901 －4920.

［8］Kesler O，Crews L K，Gibson L J.Creep of sandwich beams with metallic foam cores［J］.Materials Science and Engineering A，2003，A341:264 －272.

［9］Kesler O，Gibson L J.Size effects in metallic foam core sandwich beams［J］.Materials Science and Engineering，2002，A326:228 －234.

［10］Tagarielli V L，Fleck N A.A Comparison of the Structural Response of Clamped and Simply Supported Sandwich Beams With Aluminium Faces and a Metal［J］.Journal of Applied Mechanics，2005，72(3):408 －417.

［11］Chen C，Harte A M，Fleck N A.The plastic collapse of sandwich beams with a metallic foam core［J］.Mechanical Sciences，2001，43:1483 －1506.

［12］Harte A M，Fleck N A，Ashby M F.The fatigue strength of sandwich beams with an aluminium alloy foam core［J］.Fatigue，2001，23:499 －507.

［13］Bart-Smith H，Hutchinson J W，Fleck N A，et al.Influence of imperfections on the performance of metal foam core sandwich panels［J］.Solids and Structures，2002，39:4999－5012.

［14］Sha J B，Yip T H.In situ surface displacement analysis on sandwich and multilayer beams composed of aluminum foam core and metallic face sheets under bending loading［J］.Materials Science and Engineering，2004，A386:91－103.

［15］Tagarielli V L，Fleck N A，Deshpande V S.The Collapse Response of sandwich beams with Aluminium Face sheets and a metal foam core［J］.Advance engineering materials，2004，6(6):440 －443.

［16］ASTM Standard C393 －06.2006，Standard Test Method for Core Shear Properties of Sandwich Constructions.Philadelphia［S］.American Society for Testing and Materials.

［17］Allen H G.Analysis and Design of Structural Sandwich Panels［M］.Oxford:Pergamon Press，1969.

［18］Ashby M F，Evans A G，Fleck N A，et al.Metal Foams:A Design Guide［M］.Oxford，UK:Butterworth-Heinema nn，2000.