双参数冲击荷载作用下弹性压杆的动力屈曲研究

钟炜辉，郝际平，雷 蕾

(1.西安建筑科技大学 土木工程学院，西安 710055;2.中国电力工程顾问集团 西北电力设计院，西安 710075)

早期对轴心压杆冲击屈曲的研究方法大多以BR运动准则［1]与放大函数法［2]为主，虽然这些方法本身存在着一定的不足，且在一定程度上掩盖了屈曲问题的本质，但作为一种便于计算机计算的实用屈曲准则，仍得到广泛的应用［3，4]。而自上个世纪60年代以来，国外学者开始讨论应力波传播对冲击屈曲的影响［5，6]，国内关于应力波对冲击屈曲影响的研究，具有代表性的工作有:朱兆祥［7]通过实验研究揭示了冲击屈曲过程中的应力波效应，张善元等［8，9]就直杆冲击分岔屈曲进行的理论与实验研究，王安稳［10，11]建立的直杆弹、塑性动力屈曲能量准则并提出了特征参数方法等。

实际上，作用在实际结构上的冲击荷载往往是相当复杂的，但目前对于冲击屈曲问题的研究，其冲击荷载的形式大多集中在较为简单的理想脉冲荷载与阶跃荷载二者上，前者主要研究结构在冲击荷载作用下被激发的行为，而后者则重点对应力波传播对结构动力响应的影响进行分析。Youngdahl［12]与朱国琦［13]曾就冲击荷载形式对结构塑性动力响应的影响进行了讨论，可以预见的是，冲击荷载形式对结构动力屈曲有较大的影响。

图1 双参数冲击荷载Fig.1 Two-parameters impact load

有鉴于此，本文试采用如图1所示的非恒值冲击荷载形式——双参数冲击荷载P(t)对弹性压杆冲击屈曲进行分析，将双参数冲击荷载进行等价矩形脉冲简化，除对理想轴心压杆建立冲击分岔屈曲条件外，还对初始几何缺陷轴心压杆进行分析，并通过有限差分法进行计算，得出了双参数冲击荷载作用下弹性压杆冲击屈曲的计算方法。通过两端简支和两端固定轴心压杆冲击屈曲算例，初步揭示了冲击荷载形式对轴心压杆动力屈曲的影响规律，获得了有价值的结论。

1 双参数冲击荷载的简化

双参数冲击荷载(图1)可以表示为:

式中:Pmax为双参数荷载的最大值;tp为双参数荷载的作用时间。

对轴心压杆冲击屈曲而言，双参数冲击荷载较阶跃荷载要复杂得多，其主要原因是不同时刻不同杆件截面的受力情况并非仅与应力波的传播有关，还与双参数冲击荷载的Pmax与tp密切联系。一个简单、有效的做法就是参照Youngdahl的思路［12]将双参数冲击荷载近似看作由若干个矩形脉冲荷载组成(等价矩形脉冲，即令冲量面积与形心位置相同的脉冲来代替真实的冲击荷载形状)，再将各矩形脉冲荷载作用下的杆段组合起来，就可对双参数冲击荷载作用的轴心压杆进行近似分析，从而简化计算。如图2所示根据不同简化精度的各矩形脉冲荷载大小分别为(m表示简化的矩形脉冲荷载总数):

图2 双参数冲击荷载的简化Fig.2 Simplify two-parameters impact load

2 理想弹性压杆的冲击分岔屈曲

2.1 控制方程(组)

阶跃荷载作用下理想轴心压杆(如图3所示)的冲击屈曲控制方程(组)可以表示为:

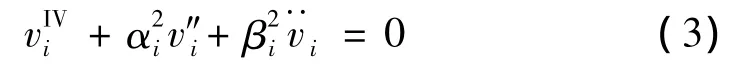
图3 阶跃荷载作用下的轴心压杆Fig.3 Axial compression bar under step load

可得:

式中:γ为一动力参数;κi=对于式(5a)，根据动力参数γ取值不同，其解呈现不同特性，当γ＜0时，为指数型发散解，形式为 T(t)=A eωt+B e－ωt(ω = －A、B为常数)，表明系统在经受微小扰动后的运动是无界的，处于不稳定状态，对应动力屈曲情况。当γ＜0(即 κi＜0)时式(5b)有解:

(Ⅲ)当4κi＜ －＜0时

2.2 连续条件

各杆段间的连续条件可表示为(定义不同应力杆段的交界处为Li，i+1，分 段 规则如图4所示):

图4 杆件分段规则Fig.4 Rule for segmentation of bar

2.3 补充定解条件

相比于静力屈曲，由于式(5a)中动力参数γ的引入，通过积分常数的齐次方程组获得的冲击分岔屈曲条件中存在着两个未知参量(P与γ)，因此类似静力屈曲建立屈曲条件的方法只能得出两个未知参量的关系而不能确定其值，有必要补充新的定解条件。根据文献［10] “直杆发生分岔屈曲的瞬间所释放出的压缩变形能等于屈曲所需变形能与屈曲动能之和”以及“在能量转换过程中能量对时间的变化率服从守恒定律”的思想，可建立关于轴心压杆的冲击分岔屈曲补充定解条件［11]:

2.4 冲击分岔屈曲条件

由式(6a)～式(6c)可知，各杆段的解Vi均有4个待定积分常数，因此可通过杆件两端4个边界条件以及各杆段间的4个连续条件，获得关于4n个积分常数的齐次方程组，进而建立冲击分岔屈曲条件，从而求得杆件在不同时刻下的冲击屈曲荷载及相应屈曲模态［14]。

2.5 理想弹性压杆的冲击分岔屈曲计算

双参数冲击荷载作用下理想弹性压杆的动力屈曲计算应根据不同的矩形脉冲荷载作用区域将杆件划分成若干个杆段，而简化的矩形脉冲荷载个数越多，荷载越精确，将使问题求解的计算量越大。

表1列出了两端简支和两端固定理想弹性压杆的首阶冲击屈曲荷载Pdcr(对应着式(1)中的Pmax)及相应动力参数ω，对比了两种荷载简化情况的影响(m分别取 1、3)，同时对荷载作用时间 tp分别取 t0.5、t1.0(即应力波传播至杆件中央和远端的时间)进行了计算。由表中可以看出，m=3的冲击屈曲荷载Pdcr相比m=1的情况略小(除两端简支tp=t1.0时)，而相应动力参数ω则偏大，这主要是因为在局部杆段上存在着相对较大的杆件应力，致使杆件容易发生屈曲，同时也使杆件的屈曲变形发展较快。

表1 理想弹性压杆的冲击屈曲Tab.1 Impact buckling of ideal elastic compression bars

3 初始几何缺陷弹性压杆的冲击屈曲

3.1 控制方程

如图5所示具有初始几何缺陷(初弯曲)的轴心压杆，其冲击屈曲控制方程为:

式中:v0为杆件的初始横向位移。由于上式不易获得精确的解析解，因此本文采用有限差分法对其进行计算。

图5 初始几何缺陷轴心压杆Fig.5 Axial compression bar with initial imperfection

3.2 有限差分格式

控制方程式(9)含有z与t两个未知量，因此对其需进行空间与时间上的离散。如图6所示将杆件沿其长度z方向等分成n段，每段长度为Δl=l/n。若设第i段末端的位移为vi，则中心差分格式为:

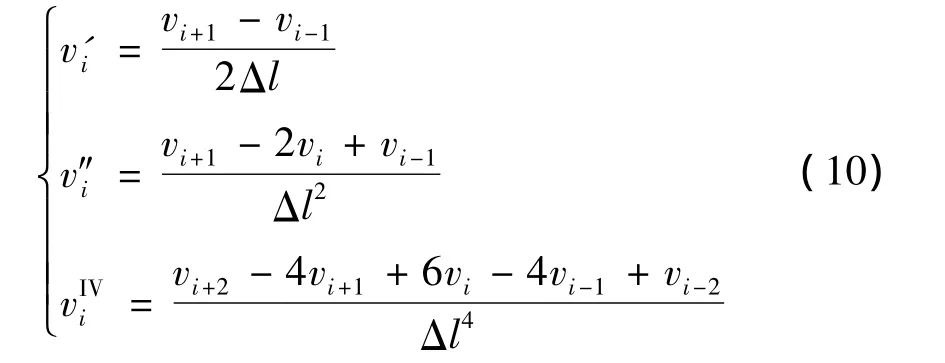
将上式代入式(9)可得第i点的差分方程:

式中:·v·表示横向位移对时间的两阶导数。图6中的v－1与vn+1可根据不同边界条件而定，若为简支则v－1=－ v1、vn+1= － vn－1，若为固定则 v－1=v1、vn+1=vn－1。

图6 有限差分法的空间离散Fig.6 Discrete space of finite difference method

其次，进行时间离散，可得k时刻各离散点位移vi，k的中心差分格式(时间步长为Δt):

将上式第二式代入式(9)可得第i点在k时刻的差分方程:

由上式可见，只要知道k及k－1时刻各离散点的位移v，就可求得k+1时刻各点的横向位移，依此类推。当k=0时，由式(12)整理可得:

上述有限差分计算时时间步长Δt的选取应小于由所求解方程性质决定的某个临界值Δtcr，否则算法是不稳定的，本文将Δtcr定义为轴向应力波在两相邻离散点之间的传播时间。

3.3 初始几何缺陷弹性压杆的冲击屈曲计算

对于两端简支和两端固定轴心压杆的初始几何缺陷形式如表2所示。表3列出了两端简支和两端固定初始几何缺陷弹性压杆的冲击屈曲系数ζ(ζ=vm/v0m，vm、v0m分别为杆件最大挠度与初始几何缺陷最大挠度)，对比了三种荷载简化情况(m分别取1、3、5)和两种冲击荷载的影响，同时对荷载作用时间tp分别取t0.5、t1.0和杆件长细比 λ 分别取 50、100 进行了计算。

表2 轴心压杆的初始几何缺陷形式Tab.2 Initial imperfection forms of axial compression bars

表3 初始几何缺陷弹性压杆的冲击屈曲Tab.3 Impact buckling of elastic compression bars with initial imperfection

由表中可以看出，荷载简化精度m对冲击屈曲系数ζ的影响不大，比较m=1与m=5的计算结果可以发现，误差通常在5%左右，且一般不超过10%，即双参数冲击荷载采用冲量相等的原则来简化计算是可行而有效的。m=1相对于m=3、5由于首先输入的应力较大，其作用在构件的时间最长，因此随着m的增大，冲击屈曲系数ζ(绝对值，后同)应会有所减小。但实际上，冲击屈曲系数ζ会随着时间t的增加而呈非线性增大，若后续输入的应力较大，则也有可能会出现冲击屈曲系数ζ随着m的增大而增大的现象。另外，冲击荷载的增加会使冲击屈曲系数ζ增大，但由于本文是在弹性小变形范围内进行计算的，因此冲击屈曲系数ζ随冲击荷载的非线性变化不明显。对于两端固定轴心压杆，初始几何缺陷1所产生的屈曲变形大多偏大。

图7 初始几何缺陷两端简支轴心压杆的冲击屈曲变形Fig.7 Impact buckling deformations of elastic compression bars with initial imperfection of both ends simple supported

初始几何缺陷两端简支轴心压杆的冲击屈曲变形如图7所示(图中纵坐标均进行了归一化处理，后同)。由图中可以看出，m=5时杆件的最大横向变形(峰值)相对于m=1偏向于冲击端，表现出双参数冲击荷载所产生的变形与阶跃荷载的差异，但二者差别不大。

初始几何缺陷两端固定轴心压杆的冲击屈曲变形如图8所示。由图中可以看出，固定边界条件将对杆件屈曲变形有重要影响，会使杆件出现较大的反向横向变形，并且随着时间的增大(应力波传播更充分)，正向横向变形发展相对迅速，且随着长细比λ的增大，该现象越显著。荷载简化精度m的变化对两端固定轴心压杆的冲击屈曲变形有一定影响，比两端简支的影响要大，这主要是由于边界条件使杆件发生较大的局部变形所造成的。

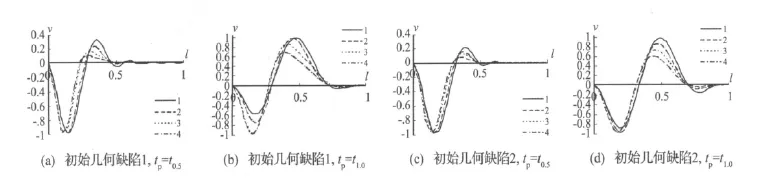
图8 初始几何缺陷两端固定轴心压杆的冲击屈曲变形Fig.8 Impact buckling deformations of elastic compression bars with initial imperfection of both ends fixed

4 结论

(1)双参数冲击荷载作用下弹性压杆的冲击屈曲问题研究可采用等价矩形脉冲的方法对荷载进行简化，本文对理想的和初始几何缺陷的弹性压杆冲击屈曲分别进行了分析和计算。

(2)双参数荷载的简化精度对理想弹性压杆冲击分岔屈曲的计算量有重要影响，从本质上看是改变了杆件不同位置处的刚度，大体上所得冲击屈曲荷载将比实际情况要小，但冲击屈曲变形发展却要快。

(3)双参数荷载的简化精度对初始几何缺陷弹性压杆的冲击屈曲计算影响较小，但当边界条件是固定时，杆件会出现显著的反向变形，此时不同情况下杆件的正、反向变形变化将有显著差异。

［1] Budiansky B，Roth R S.Axisymmetric dynamic buckling of clamped shallow［A] .NASA-TN －1510，1962，597－609.

［2] Goodier J N.Dynamic plastic buckling［A] //dynamic stability of structure［M] .Ed.by Hermann G.，1967:189－211.

［3] Ari-Gur J，Weller T，Singer J.Experimental and theoretical studies of columns under axial impact［J] .Int.J.Solids Struct.，1982，18(8):619 －641.

［4] 王德禹.受静载作用的直杆在轴向冲击载荷下的屈曲［J] .振动与冲击，1997，16(1):35－37.

［5] Abrahamson G R，Goodier JN.Dynamic flexural buckling of rods within an axial plastic compressive wave［J] .ASME Journal of Appl.Mech.，1966，33:241 －247.

［6] Lindberg H E.Impact buckling of a thin bar［J] .J.Appl.Mech.，1965，32:315 －322.

［7] 汤立群，朱兆祥.弹性直杆动态屈曲与后屈曲的实验研究［J] .爆炸与冲击，1998，18(2):97－102.

［8] 张善元，王 蕊，韩志军.直杆动力屈曲及屈曲过程中的应力波效应［J] .太原理工大学学报，2007，38(1):1－4.

［9] 张善元，程国强，韩志军.弹性杆稳定性动力分析与应力波加载杆的动力屈曲［J] .太原理工大学学报，2005，36(2):111－114.

［10] 王安稳.弹性压应力波下直杆动力失稳的机理和判据［J] .力学学报，2001，33(6):813－820.

［11] 王安稳.直杆塑性动力屈曲的双特征参数解［J] .固体力学学报，2004，25(3):255－261.

［12] Youngdahl C K.Interaction between pulse shape and strain hardening in dynamic plastic response［J] .Int.J.Impact Engng.，1988，7(1):55 －70.

［13] Zhu G Q，Huang Y G，Yu T X，et al.Estimation of the plastic structural response under impact［J] .Int.J.Impact Engng.，1986，4(4):271 －282.

［14] 钟炜辉，郝际平，雷 蕾，等.考虑应力波的轴心压杆冲击分岔屈曲研究［J] .振动与冲击，2010，29(10):201－205.

［15] 钟炜辉.冲击荷载作用下轴心受压构件动力屈曲研究［D] .西安:西安建筑科技大学，2009:77－78.