多类别交通网络的Wardrop型原理

王 利，杨青骥

(1. 上海第二工业大学，上海 201209；2. 上海金融学院应用数学系，上海 201209)

多类别交通网络的Wardrop型原理

王 利1，杨青骥2

(1. 上海第二工业大学，上海 201209；2. 上海金融学院应用数学系，上海 201209)

研究了有容量约束的网络中有限多类别用户形成的均衡。在考虑容量约束的网络中，结合用户的异质性来分析广义通行费用、实际通行费用；结合路径的饱和性，将经典的Wardrop原理推广到有容量约束的多类别的Wardrop型原理。

多类别；容量约束；通行费用；Wardrop型原理

0 引言

1952年，英国交通工程师J. G. Wardrop 提出了两个基本原理[1]。

第一原理：在交通网络的每一对起-终点之间，有人走的路径上的通行时间都是相等的，并且少于没有人走的路径上的通行时间；

第二原理：对于给定的交通网络，管理者的目标是最小化平均的通行时间。第一原理基于用户的理性假设：网络中的用户总是尽可能地最小化自己的通行时间。所有的用户都如此选择的结果形成了用户均衡 (user equilibrium)。第二原理假设用户是合作的，从而保证总的通行时间最少。

然而，由于容量约束的引入，Wardrop第一原理不再适用。在研究容量约束下的交通网络均衡的文献中，有一些研究工作者着手于推广网络均衡的定义并分析相应的均衡性质。比如，1994、1997年，Maugeri等给出了考虑路径上容量约束的广义用户均衡（Generalized User Equilibrium）[2]、扩展Wardrop均衡 ( Extended Wardrop Equilibrium)[3]；1994～1999年，Larsson和Patriksson定义了在广义通行费用下的Wardrop均衡（Generalized Wardrop Equilibrium），研究了有附加限制（side constraints）的交通均衡模型，给出了均衡解的性质、广义费用的性质等[4-6]。但是这些研究并未考虑到网络中用户的异质性。

在交通问题的研究中，有很多学者关注网络中用户的异质性。1972年，Dafermos 研究了多类别的交通问题，认为不同类别的用户有不同的成本函数[7]。用户在选择最佳出行路径时可能面对着多种准则的考虑，如通行时间、通行费用等。一些学者引入时间价值（value of time, VOT）参数作为一种权重因子，它将通行时间转化为货币单位。VOT参数取值为离散数值，意味着网络中所有用户被分成有限个类别，每一类用户有一个相同的时间价值。近些年来，很多学者对多类别、多准则的交通网络均衡问题及应用进行了研究，如参考文献[8-10]等。

本文试图在考虑容量约束的网络中，结合用户的异质性来分析广义通行费用、实际通行费用；结合路径的饱和性将经典的Wardrop原理叙述推广到有容量约束的多类别的Wardrop型原理。在第一节中，将介绍多类别的交通网络及广义Wardrop均衡的相关结论；第二节中，给出了在有容量约束的网络中，刻画多类别用户均衡的Wardrop型原理。

1 多类别的交通网络

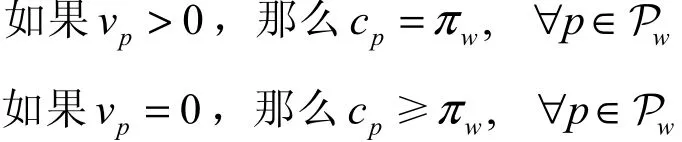
这里的pv表示路径p上的流量，pc表示路径p上的通行时间，wπ表示路径p所连接的OD对w之间的最短通行时间。

现在考虑用户依据两种准则——通行时间和通行费用（收费），来选择自己的出行路径。设是第m类用户的时间价值，相应的交通需求被分为M类，对每是网络中第m类用户的用户需求构成的向量。假设d(m)是给定的。

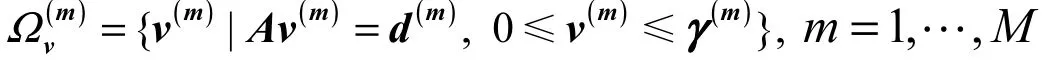
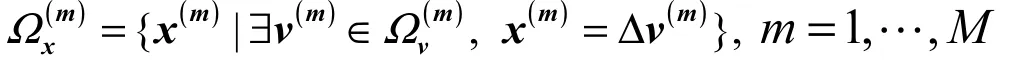
其中∆是路段-路径之间的关联矩阵，当路段a在路径p上时，其元素路径、路段上所有类别的用户构成的可行流向量集合分别为

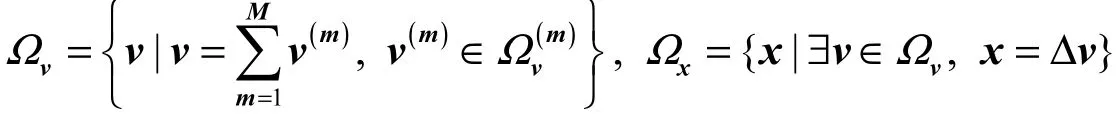
路段上的流量受到的约束为

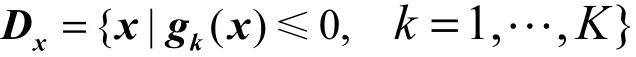
其中每一kg()x都是连续可微的凸函数，这K个函数构成向量()gx。这些约束可以转化成路径上的限制，

在路径p、路段a上的通行时间函数分别记为cp(v), ta(x)，根据可加性，有或向量-矩阵形式构成的向量。设及相应的满足下列变分不等式(Variational Inequality，简记为VI)

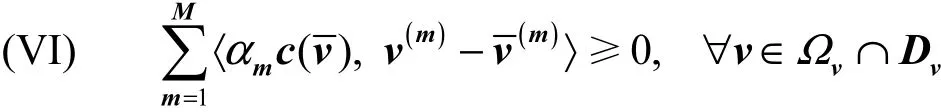
或路段流量表示的等价形式

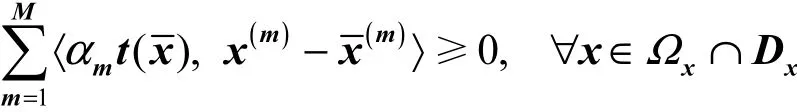
为方便起见，不加区别地用S (VI) 表示 (VI) 路径流量形式的解集或者等价的路段流量形式的解集，记其中的解为

引理1.1 变分不等式(VI)的解存在。

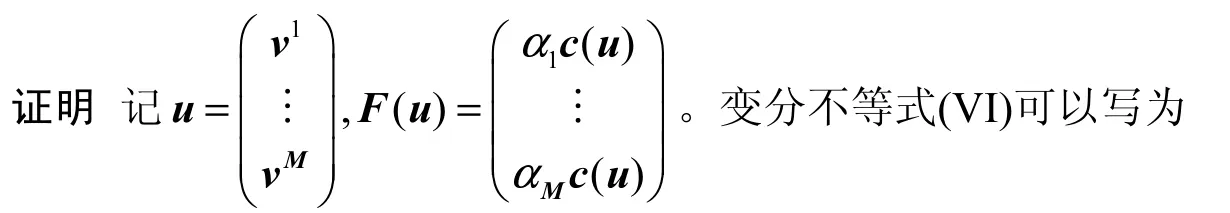
其中u属于某个紧集合，F是一个连续的向量函数。由变分不等式理论(见参考文献[11]等)得到(1)式的解存在，也即(VI)的解存在。 证毕

变分不等式(VI)的解等价于优化问题

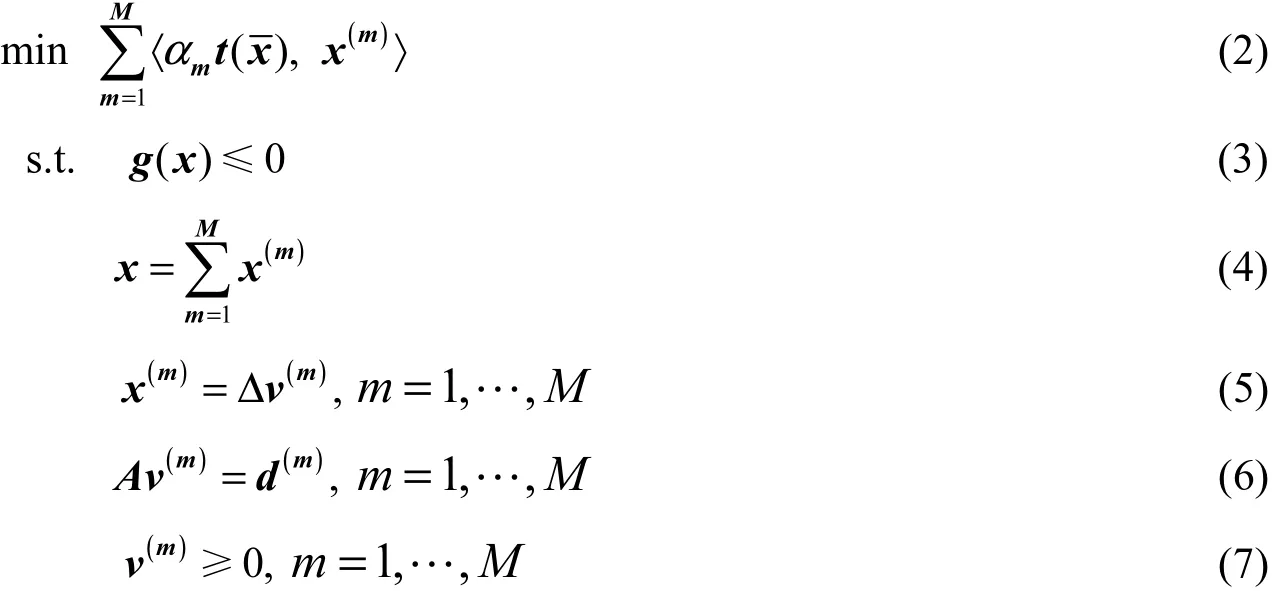
的解。下文中提到的(VI)的约束

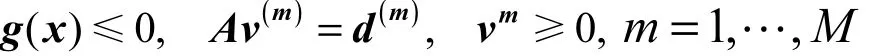
的乘子总是指在优化问题(2)式～(7)式中的相应乘子。

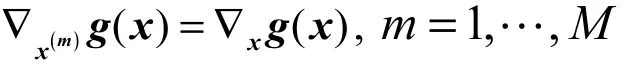
为方便起见，统一记为()gx∇。

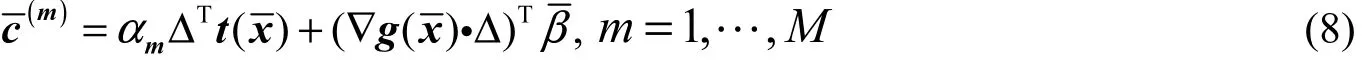
则称**

(,)xv是多类别交通网络的广义Wardrop均衡(MGWE)。

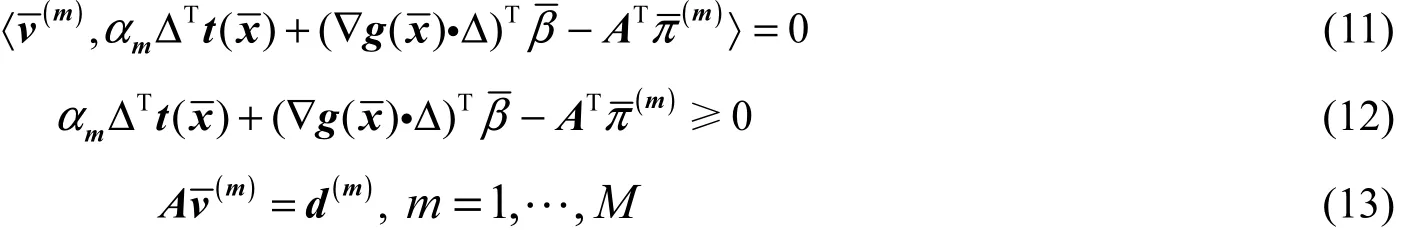
因而对于任意的OD对w∈W，由条件(11)式～ (13)式得到是OD对w之间第m类用户的最低广义通行费用；并且在OD对w之间所有第m类用户通过的道路上，此类用户的广义通行费用是相等的。因此，条件(9)式、(10)式成立，即定理结论成立。

2 Wardrop型原理

这一节中，首先给出不饱和的定义及相关的假设；然后得到不饱和路径上惩罚费用的性质；最后证明用实际费用描述的Wardrop型原理。

则称路段a∈A是不饱和的。如果在路径r上的全部路段都是不饱和的, 则称该路径是不饱和的。

显然，由这个定义可以得到：在x∈Ωx∩Dx处，如果路径r饱和，则存在其上的某个路段a及某个k, 有

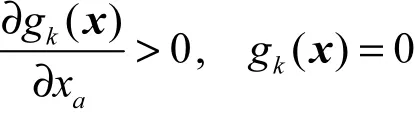
成立。

对于不饱和的路径，有如下结论：

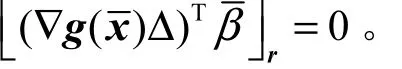
证明 设路径r通过的路段为a1,…,aI。 在∆的第r列∆·r中,

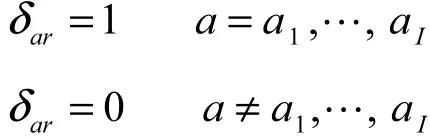
路径r上的惩罚费用

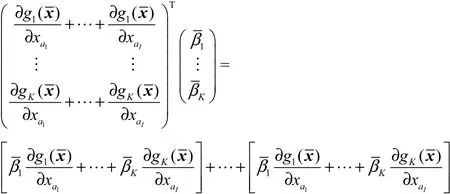
或

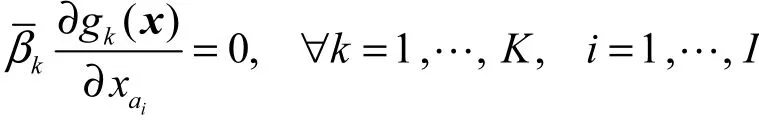
成立，从而可以得到结论成立。 证毕

接下来，给出多类别网络中用实际通行费用描述用户均衡的结论。

1) 在OD对w之间，有第m类用户通过的路径上该类用户的广义通行费用相等且为最低；

2) 假设在OD对w之间的某ml条路径（不妨设为前ml条）上有第m类用户通过，而且其中的ms条路径是不饱和的，则这些路径可以如下排序

证明 1) 根据定理1.1可以得到结论。

2) 由(1)式可以得到有第m类用户通过的ml条路径（其中，前ms条路径不饱和）上，该类用户的广义通行费用相等, 即

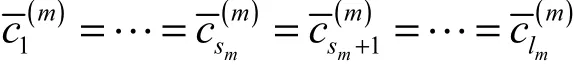
根据假设2.1、定义2.1及引理2.1，在不饱和的路径上，有。 所以，

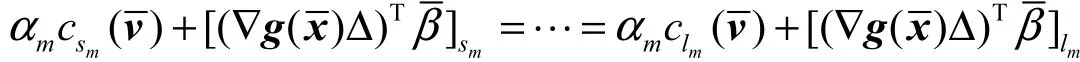
定义1.2其实是将经典Wardrop原理中的实际通行费用换为广义通行费用来刻画容量约束下的多类别用户均衡。在定理2.1中，仍然用实际费用，只是借助了更接近于现实的概念——饱和性来刻画多类别用户均衡，称之为Wardrop型原理。

[1] WARDROP J G. Some theoretical aspects of road traffic research[J]. ICE Proceedings: Engineering Divisions, 1952, 1(3): 325-362.

[2] MUGERI A. Optimization problems with side constraints and generalized equilibrium principles[J]. Le Matematiche, 1994, 49(2): 305-312.

[3] MUGERI A, OETTLI W, SCHLAGER D. A flexible form of wardrop's principle for traffic equilibria with side constraints[J]. Rendiconti del Circolo Matematico di Palermo, Serie 2, Supplement, 1997, 48: 185-193.

[4] LARSSON T, PATRIKSSON M. Equilibrium characterizations of solutions to side constrained asymmetric traffic assignment models[J]. Le Matematiche, 1994, 49(2): 249-280.

[5] LARSSON T, PATRIKSSON M. An augmented Lagrangean dual algorithm for link capacity side constrained traffic assignment problems[J]. Transportation Research Part B: Methodological, 1955, 29(6): 433-455.

[6] LARSSON T, PATRIKSSON M. Side constrained traffic equilibrium models—analysis, computation and applications[J]. Transportation Research Part B: Methodological, 1999, 33(4): 233-264.

[7] DAFERMOS S C. The traffic assignment problem for multiclass-user transportation networks[J]. Transportation Science, 1972, 6(1): 73-87.

[8] YANG H, HUANG H J. The multi-class, multi-criteria traffic network equilibrium and systems optimum problem[J]. ransportation Research Part B: Methodological, 2004, 38(1): 1-15.

[9] HUANG H J, LI Z C. A multiclass, multicriteria logit-based traffic equilibrium assignment model under ATIS[J]. European Journal of Operational Research, 2007, 176(3): 1464-1477.

[10] ZHANG X, YANG H, HUANG H J. Multiclass multicriteria mixed equilibrium on networks and uniform link tolls for system optimum[J]. European Journal of Operational Research, 2008, 189(1): 146-158.

[11] KINDERLEHRER D, STAMPACCHIA G. An Introduction to Variational Inequalities and Their Applications[M]. New York: Academic Press, 1980.

Wardrop-Type Principle in Finite Multiclass Traffic Network

WAN G Li1, YANG Qing-ji2
(1. Shanghai Second Polytechnic University, Shanghai 201209, P.R.China；2. Department of Applied Mathematics, Shanghai Finance University, Shanghai 201209, P.R.China)

Equilibrium of finite multiclass customers in traffic network with capacity constraints is considered. For the network, generalized and actual travel cost are analyzed by combining with heterogeneity of customers. The classical Wardrop principle is reformulated as Wardrop-type principle in finite multiclass traffic network by introducing the saturation of path flow.

finite multiclass; capacity constraint; travel cost; Wardrop-type principle

O22

A

1001-4543(2011)04-0325-06

2011-09-12;

2011-12-19

王利（1977－），女，河南洛阳人，讲师，硕士，主要研究方向：运筹学应用，电子邮箱wangli@sspu.cn。