多响应线性模型的Bayes E-最优设计

王 帅，岳荣先，付 清

(上海师范大学 数理学院，上海 200234）

0 引言

对于单响应线性模型的Bayes E-最优设计的等价定理，Pilz已经给出了详细的讨论，但对于最优设计的算法，文章并没有给出。本文拟在单响应模型的基础上，将其理论推广到Bayes多响应线性模型中，并建立Bayes E-最优设计的等价定理和相应的迭代算法，这将更有利于应用到实际当中。

考虑有r个响应的线性模型，它可以表示为如下形式：

χ为设计区域，fi(x)是pi维的列向量，βi是pi×1维的未知参数向量，εi是与第i个响应yi有关的随机误差，且当i≠j时，εi与εj相关。我们假定随机误差满足下列关系：

记Xi=(fi(x1),fi(x2),…,fi(xn))T为n×pi阶 矩 阵 ，X=diag(X1,X2,…,Xr)为nr×p阶矩阵。则模型可以表示为Y=Xβ+ε。

1 Bayes估计与设计准则

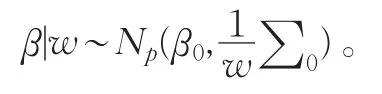
若vn=(x1,x2,…,xn)表示n个点的试验设计，且每个点的实验测度都相同为1n，则在精确设计和后验密度下，我们定义信息阵为：

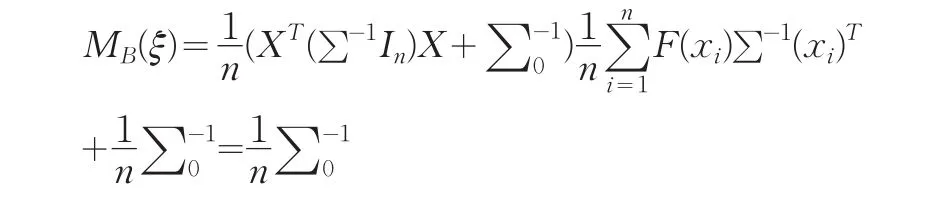
记Ξ为定义在设计区域χ上的概率测度的全体，ξ∈Ξ为连续设计，则其对应的信息阵为：

2 Bayes最优设计的等价定理

对任意ξ∈Ξ ，令λξ=λmin(MB(ξ))，即λξ为对应的Bayes信息阵的最小特征值，假定它为简单特征值，且它对应的特征向量为Vξ。

定理1对于Bayes情况下的E最优准则，我们简记为EB最优准则，它对应的Frechet导数记为FEB，则：

(1)FEB是线性的；

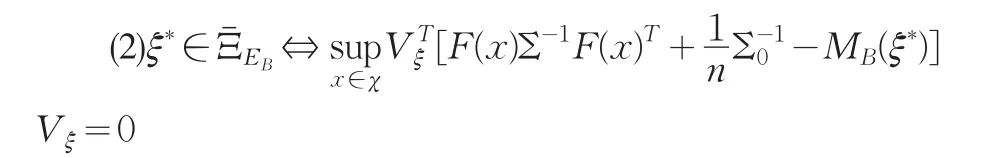
证 明 ：(1) 因 为λmax(MB(ξ)-1)=1/λξ，所 以 ，使EB(·):=λmax(MB(·)-1) 达 到 最 小 就 等 价 于 使B(·):=-λmin(MB(·))达到最小。求解的Frechet导数如下：

得证。

(2)因为Bayes信息阵是正定的，所以它的特征值全为正，所以将(i)两边同除以EB(ξ)，不等号的方向不变，即有：

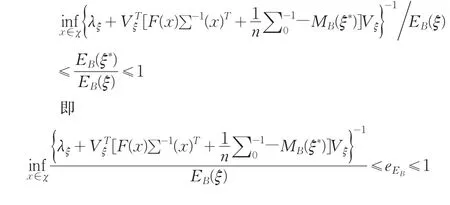
3 Bayes E-最优设计的迭代算法

假设任意选取n0个点，(x1,x2,…,xn0)∈χ作为初始设计点，则

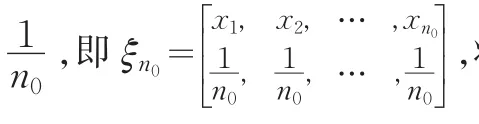
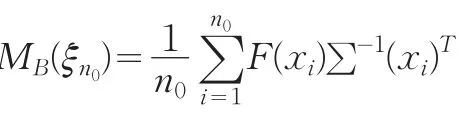
（2）计算设计ξn0的效率的下界：

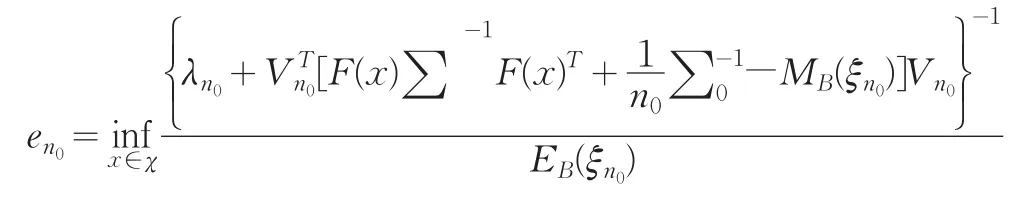
（3）预先给定常数e0，判断，若en0＜e0则进行第二步；若en0＞e0则初始设计的效率已满足要求，但这种情况通常不会发生。

第二步：对n≥n0，令n=n+1。

（1）寻找第n+1个点，使它满足：

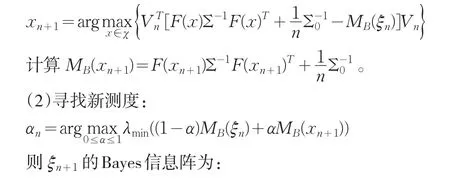
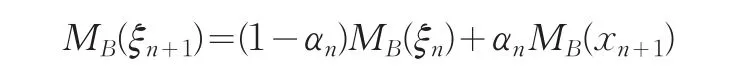
第三步：(1)令λn+1=λmin(MB(ξn+1))，即为第n+1 步Bayes信息阵的最小特征值，而Vn+1为λn+1对应的标准特征向量；

（2）计算

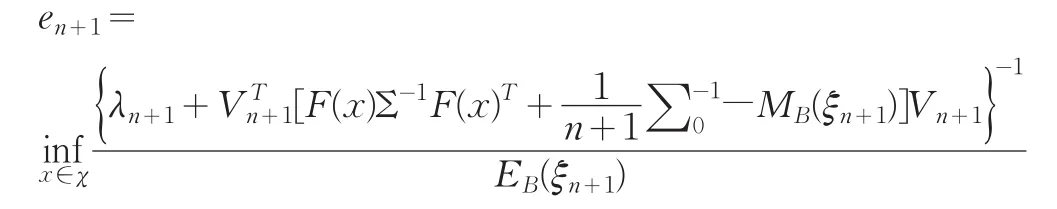
若en+1＜e0则继续进行第二步，否则停止迭代。

例：考虑两个响应的可控变量模型，假设实验区域为χ={x=(x1,x2): ||xi≤1,i=1,2}，给定e0=0.9，建立模型：

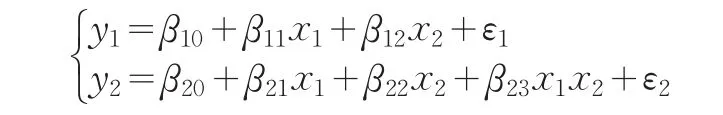
β服从先验分布N(β0,Σ0)，这里β的先验协方差矩阵为Σ0=diag(Σ01,Σ02)，其中

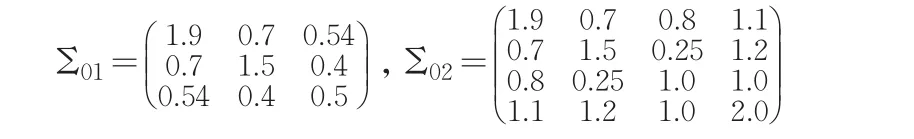
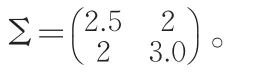
应用上述算法迭代之后，得到的设计点和它们对应的测度为：

这个例子得到的设计点均在设计区域的端点处取得，符合最优设计的理论。同时也证明了以上算法的可行性，通过不断的增加设计点，使得EB最优设计效率的下界0.5012增加到0.9749，并且效率的增加也比较稳定。在更加复杂的实际运用中，迭代算法同样也有其适应性。

[1]Pilz J.Bayesian Estimation and Experimental Design in Linear Regression Models[M].Feiberg:Tenbuer Leipzig,1983.

[2]汪倩菁,岳荣先.多响应线性回归模型Bayes最优设计的等价性定理[J].上海师范大学学报(自然科学版)，2008，37(3).

[3]Zellner A.An Efficient Methodof Estimating SeeminglyUnrelated Regressions and Tests for Aggregation Bias[J].J.Amer.Statist.Assoc,1962,（57）.

[4]张丹,岳荣先.多响应线性模型最优设计的迭代算法[D].上海:上海师范大学，2008.