超出损失保险的纯保费估计和风险度量

欧阳资生

（湖南商学院金融学院，长沙 410205）

0 引言

根据瑞士Sigma杂志统计，自1990年以来全球巨灾损失(包括自然灾害和人为灾祸)发生变得更加频繁和严重。巨大的保险损失给国际保险业带来了新的挑战，严重威胁着保单持有者的利益。单纯的依靠保险业自身的实力已经无法应对这些巨灾风险，保险公司的承保能力急剧下降，保险公司和保险监管部门亟待研究制定新的巨灾保险费率的方法以解决这些保险公司的赔付能力。

当然，保险业发展至今日，其风险转移的方式已多样化，如再保险、保险衍生证券等都已经成为很好的风险转移的方式。在再保险中，精算师研究的实际上就是超出损失保险(Excess-of-Loss)(简称XL)的纯保费问题。在XL中，被保险人只能对超出某一固定值(门限值)的损失部分提出索赔要求。这时，纯保费就是下一个时期内总索赔数目的期望值。如果设SN为下一个时期内总索赔数目，N是下一个时期内索赔额超出某一固定值u的索赔次数，Zi为超出u的索赔额，Xi表示索赔额超出固定值u的该张保单的索赔额。那么,Zi=Xi-u。而下一期总索赔数目就是

因此纯保费就是E[SN]。

对于式（1）的研究，至少涉及到两个方面，一是索赔次数N的估计问题，目前文献中索赔次数大多采用Poisson过程来描述。事实上，如果N为服从一参数为λ的Poisson过程。显然，此时纯保费就是E[SN]=λm(F)(这里m(F)表示Zi的分布F的均值)。二是对超出某固定值的索赔额Zi的分布的刻画问题。考虑到索赔数据的厚尾性，目前在索赔额Zi的分布的描述，多采用极值分布，如广义Pareto分布、全Paretian分布来刻画。本文的目的在于通过适当选取索赔次数和索赔额的分布对超出损失保险的纯保费进行合理估计，并对其风险进行度量。

1 负二项分布模型及其参数估计

在保险精算中，索赔次数N服从时齐的Poisson分布已被广泛使用,但是严格说来，Poisson分布只适应同质性保单组合。所谓同质性是指一个保单组合中每份保单具有相同的索赔频率，且相互独立。但是在许多保险中，这种同质性并不能保证成立，而是往往表现出非同质性和相关性。所谓非同质性是指保单组合中每份保单的索赔频率并不相同，而相关性是指一次保险事故的发生有可能导致多份保单的同时索赔。保单组合的非同质性和相关性在保险实践中并不少见，特别是在火灾保险和汽车保险中的情况更是如此。例如在一家保险公司投保的两车在道路上发生碰撞且各负部分责任；在火灾保险中，一次火灾可能引起多家被保险人的同时索赔等。因此，我们采用能反映这种非同质性和相关性的负二项分布模型作为索赔次数N的分布。

现在我们假定在一个给定的时间内，保单持有者的索赔次数K服从参数为λ的Possion分布，而参数为λ又服从参数为(α,β)的Gamma分布，这时保单持有者的索赔次数K就服从一负二项分布。事实上，负二项分布是Poisson分布在Gamma分布作为结构函数时的混合分布。因此，它属于混合Poisson分布，它的一个显著特征就是其方差大于均值。因此，当保单组合的索赔次数的观察值的样本方差大于其均值时，即可断定此保单组合存在某种程度的非同质性。而且方差越大，这种非同质性越严重。

现在来考虑负二项分布的概率函数，负二项分布的概率函数为：

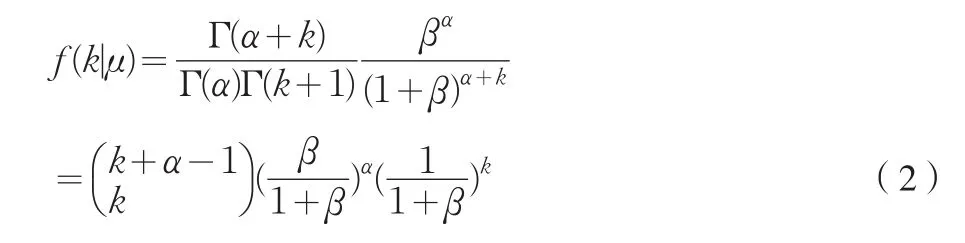
其中，k=0，1，2，…；μ＞0为过去时间内保单持有者的平均索赔次数,即E(K|μ)=μ=α/β，而参数α通常用来度量个体的索赔特征。它是一个大于零的未知常数,并且我们一般假定对所有的个体而言，α的值是相同的。索赔次数K的方差为σ2(K|μ)=μ(1+1/β)。 因此，β决定了负二项分布相对于Poisson分布的过分分散程度。平均索赔次数μ越大，负二项分布越过度分散；β越大，过度分散程度越小。当β→∞时,f(k|μ)趋向于均值为μ的Poisson分布。

现在我们来探讨保单组合在t年内发生了k1,k2,⋅⋅⋅,kt次索赔的条件下（其中ki表示第i年的索赔次数），下一年度该保单组合发生索赔的索赔次数K的最优估计。这里我们采贝叶斯估计方法进行估计。事实上，由贝叶斯定理，我们很容易得到参数λ的后验分布为：

如果我们用+1表示在第(t+1)年时对索赔频率λ的后验估计，记Ft+1(+1,λ)为用t+1估计λ的损失，它是一个关于估计误差(λt+1-λ)的非负函数，称为损失函数。则我们希望下式（即平均损失）达到最小：

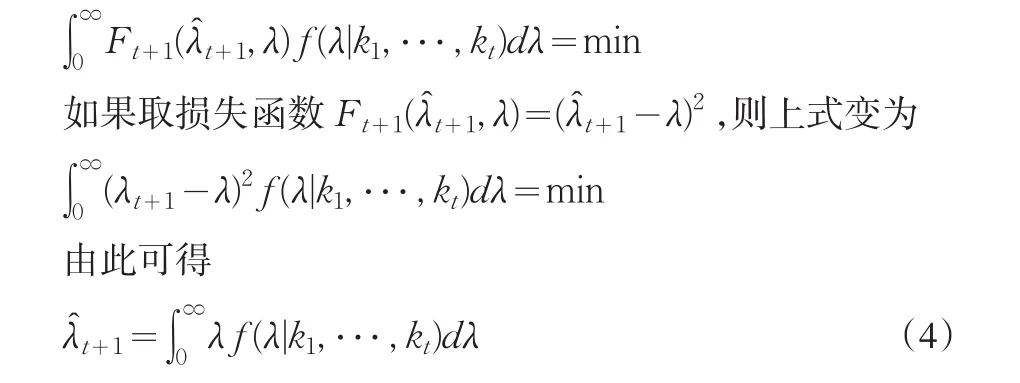
式(4)表明，当前t年的索赔次数为k1,k2,⋅⋅⋅,kt时，第(t+1)年的关于参数λ的最优估计为其后验均值。由于参数λ的后验分布为(α+Lt,β+t)的Gamma分布，因此第(t+1)年的关于参数λ的最优估计为：

2 全Paretian分布模型和超出损失保险的纯保费估计

为方便记，我们将考虑Zi的标准化形式Yi=Zi/u。这时,我们参照Reiss and Thomas(1999,2002)，欧阳资生(2006)的做法，假设Yi服从形状参数为α，刻度参数为σ的全Paretian模型，即：

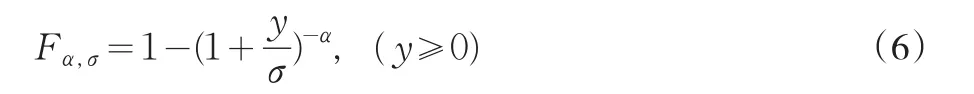
这里,α＞0,σ＞0。在式(6)中，若σ=1，我们称这个子模型为限制的Paretian模型。此时，极值指数α的HIll估计就是极大似然估计。

在式(6)中，可进一步看到为什么Hill估计及其相关估计是不精确的。事实上,刻度参数σ＜1越小,形状参数就越大，分布函数Fα,σ的右尾越厚。如果这时对分布函数进行估计,然而σ=1却固定不变，那么由刻度参数σ＜1较小引起的厚尾就必须以低估形状参数α作为补偿，更详细的介绍参见Reiss and Thomas(1999,2002)。

我们首先讨论全Paretian模型的参数进行估计方法。这里采用极大似然估计方法对其参数进行估计。由式(6)，可得Yi的密度函数为：

其对数似然函数为：

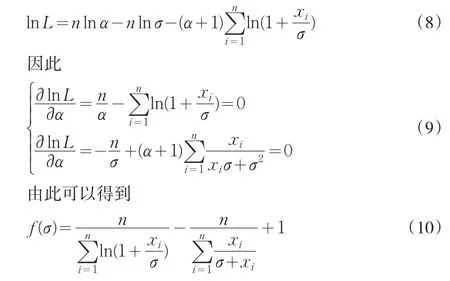
由上式通过反复迭代，即可得到参数σ的估计值，从而估计出参数α的值，即

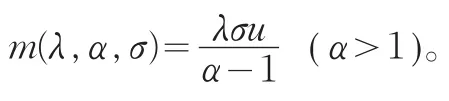
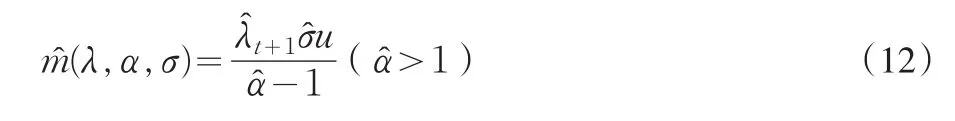
3 超出损失保险的极值风险度量

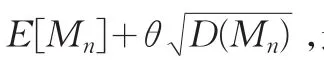
这里，ε为任意小的正数。式(13)意味着PML事实上就是一个样本容量为n的随机样本的高分位数。由于最大值Mn超出所定义的PML的可能性只有100ε%，因此

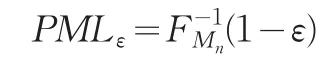
所以，PML事实上就是在一段时间内的最大损失的分布的(1-ε)的分位数。为运用这个公式，Wilkinson（1982）提出了一个基于顺序统计量的非参数方法。Kremer（1994）运用广义Pareto分布模型考虑了这个问题，Cebrian(2003)，欧阳资生（2006）在Kremer（1994）基础上进一步考虑了这个问题，并得出了PML的估计式为：

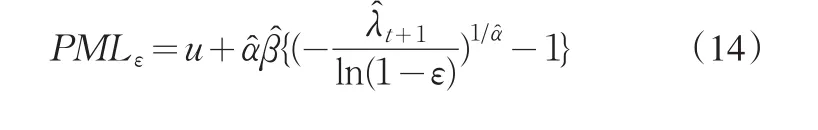
4 火灾保险的索赔数据的实证研究

结合前面的超出损失保险的纯保费估计和风险度量方法，在这里，我们利用丹麦火灾保险索赔数据进行实证分析。

4.1 索赔数据的基本描述

现在对丹麦某保险公司的火灾保险索赔数据进行分析，该数据包含了从1980年1月3日至1990年12月31日共2167个赔付额超过一百万丹麦克朗的火灾保险数据。为对数据有一基本了解，我们在表1中给出了索赔数据的基本统计特征。

表1 索赔数据的描述 单位：百万克朗

从表1可以看出，75%分位数与25%分位数的差并不大，但是数据库中包含一些损失额相当大的数据(最大的损失达263.25百万克朗)。并且数据严重右偏，偏度系数达18.76282。因此,我们选择对数刻度的直方图(见图1)，发现即使观察对数刻度的直方图，图形还是右偏的。因此认为数据具有较严重的厚尾性和右偏特征，采用全Paretian模型来刻画是合理的。

4.2 索赔数据的分布估计

首先对索赔数据的索赔频率进行估计，由参数为(α,β)的Gamma分布的均值μ=α/β,σ2=μ(1+1/β)。采用矩估计，很容易得到参数为λ服从参数为(50.11493，3.930964) 的Gamma分布，在式（5）中 ，因t=11，Lt=1267 立即可得λt+1=197。

4.3 全Paretian模型参数估计和超出损失保险纯保费的估计

我们通过式（10），采用迭代法，可求得σ=13.641，再利用式（11），很容易可以计算出α=5.368816，因此超出损失Yi服从如下全Paretian模型,即：

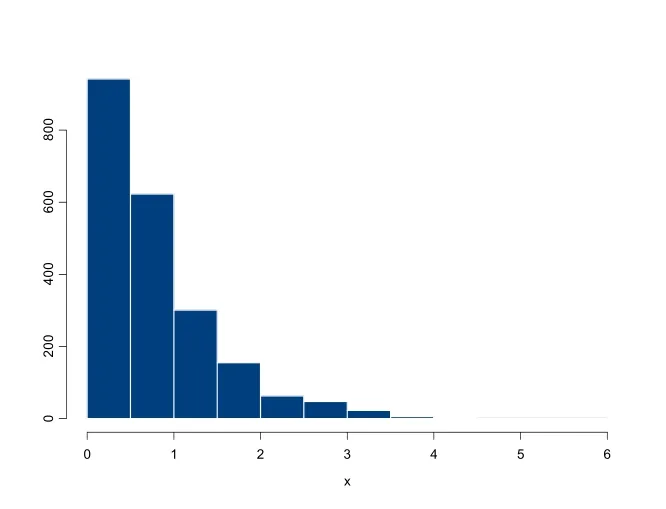
图1 索赔数据的直方图(对数刻度)1

由式（12），在下一年度，超出一百万克朗的超出损失保险的纯保费为m(λ,α,σ)=615.1042百万克朗。

4.4 可能最大损失的估计

将本文的模型参数拟合的结果应用于式（14），同时，注意到λt+1=197，立即可得索赔数据的5%、1%、0.1%的PML的点估计，具体结果见表2。从表2可以看出，火灾最大损失额为268.4537百万克朗的可能性为5%，最大损失额为389.304百万克朗的可能性为1%，最大损失额为637.0735百万克朗的可能性为0.1%，可能性为1%和0.1%的最大损失额均比这11年的最大损失263.2504百万克朗大很多。

表2 保险数据PML的点估计 （单位：百万克朗）

[1]欧阳资生.极值估计在金融保险中的应用[M].北京：中国经济出版社，2006.

[2]Cebrian,A.C.,Denuit,M.，Lambert,P.Generalized Pareto Fit to the Society of Actuarie's Large claims Database[J].North American Actuarial，2003，(3).

[3]Embrechts,P.，Klauppelberg,C.，Mikosch,T.Modeling Extremal Events for Insurance and Finance[M].Berlin:Springer,1999.

[4]Hesselager,O.A Class of Conjugate Priors with Applications to Ex cess-of-loss Reinsurance[J].Astin Bulletin，1993，(23).

[5]Kremer,E.More on the Probable Maximum Loss[J].Mathematics and Statistics,1994,21(3).

[6]Ouyang zisheng,Xiechi.Generalized Pareto Distribution Fit to Medical Insurance Claims Data，Applied Mathematics[J].A Journal of China University,2006，(1).

[7]Reiss,R.D.,Thomas,T.A New Class of Bayessian Estimations in Paretian Excess-of-loss Reinsurance[J].Astin Bulletin ，1999，29(2).

[8]Reiss R.D.,Thomas,M.Statistical Analysis of Extreme Values[J].MSOR Comections,2002,2(2).

[9]Reiss R.D.,Thomas,M.Bayesian Extreme Value Analysis with an Application to Credibility Estimation[C].9th Symposium on Finance,Banking,and Insurance.Universitaat Karlsruhe(TH),2002.

[10]Wilkinson,M.E.Estimating Probable Maximum Loss With Order Statistics[C].Proceedings of the Casualty Actuarial Society.LXIX,1982.