基于MS-VAR模型的就业影响因素非线性估计

罗孝玲，杨 立，杨怀东

（中南大学 商学院，长沙 410083）

0 引言

当前，就业问题已经成为经济发展中最重要的问题之一，国内外对此进行了广泛的研究。国外对就业问题的代表模型有贝弗里奇的结构性失业模型和菲利普.阿吉翁等提出的就业失业模型，总体上而言西方经济学观点认为经济增长是就业增长必然会带来就业增长【1】。刘新卫【2】利用道格拉斯生产函数验证了我国经济增长与就业的正相关关系。Pissarides【3】的研究表明，在劳动生产率处于上升阶段时，增加劳动力会增加企业利润，从而带来就业增长。何静慧【4】以浙江为例，研究了经济增长和技术进步对就业的影响。张晓旭【5】运用偏离—份额方法分析1978年以来中国就业增长与产业结构变迁的关系，结果发现，对于就业增长而言结构成分占主导性作用。李晓嘉等【6】分析了我国产业结构和就业结构之间的互动关系，发现我国就业矛盾的原因主要在于我国的产业结构与就业结构不相称，就业结构滞后于产业结构的发展。吴小松等【7】根据SDA模型对1987～2002年间我国就业增长与结构变迁的影响因素进行了实证分析从三次产业来看，第一产业的居民消费、第二产业的资本形成及第三产业的政府消费对各产业就业增长均有较大拉动作用。冉光和等【8】经验分析出资本投入与劳动供需协调之间存在稳定的正相关关系,技术进步则与劳动供需协调呈稳定的负相关关系,偏离比较优势的资本深化与技术进步弱化了就业促进功能并加速了劳动市场的分化。总体而言，国内外学者对就业问题进行了一系列的定性和定量分析，取得了阶段性成果。

然而，由于宏观经济运行在特定经济周期可能存在结构性变化或者结构性断点，采用传统的线性模型来研究就业的影响因素问题可能导致较大的偏差。因此，本文试图摒弃传统的线性建模思路，从研究变量的非线性特征入手，结合Ham ilton【9】分析宏观经济的思路，将我国宏观经济分为两个状态（扩张期和收缩期）进行研究。具体而言，本文运用格兰杰因果关系检验和逐步回归模型得到就业的主要影响因素，选择非线性马尔科夫状态转移向量自回归模型（MS-VAR模型）研究不同状态下就业与各个影响因素之间的关系，并在此基础上研究就业在各个状态下的转换概率和状态持续时间，从而为就业政策的提出提供理论支持。

1 就业水平影响因素的指标体系建立

1.1 就业问题评价指标（因变量Y）选取

就业是社会、国民经济中极其重要问题。按已有研究，就业可以定义为三个月内有稳定的收入或与用人单位有劳动聘用关系。本文是对就业人数进行研究，所以选取就业人数作为就业问题评价指标。

1.2 影响因素指标体系建立

影响就业的因素可能有很多，这些因素之间内部可能也存在相互之间的关系，如何系统明了地对这些因素进行分析，找到主要的影响因素的首要条件是建立合理的指标体系。

1.2.1 指标体系建立方法选取

通过参考各关于指标体系的文献，本文采用分层模式指标体系，将整个指标体系分为三层，第一层为目标层，第二层要素层，第三层为指标层；根据对各类指标的定性分析，可以认为该问题采用分层模式指标体系的目标层为“影响因素”。接下来讨论研究要素层各要素的选取和定义。

1.2.2 要素选取

参考我国宏观经济指标体系，和讯网数据库和研网数据库，以及从宏观角度看，消费、投资、政府购买和进出口都是影响就业的重要因素，再综合文献中的资料，可以提取以下可能影响就业的因素：

①消费；②投资；③对外贸易；④GDP和人口数等国民经济核算指标；⑤经济景气指数。

在进行统计分析的过程中，各要素之间可能会存在相互之间的关系，所以要对以上五个要素进行筛选。本文选取就业影响的指标体系要素层的三个要素分别为：①消费；②投资；③对外贸易。

1.3 各要素主要指标初步选取

1.3.1 消费要素

根据宏观经济核算指标，了解到反映其消费要素的指标可能有：居民消费价格指数、衣着价格指数、粮食价格指数、居住价格指数、交通和通信价格指数，社会各种消费品零售总额和居民收入等。由于衣、食、住、行价格指数综合起来就是居民消费指数，所以这几个指标就可以选择居民消费价格指数；社会消费品零售总额可以代表社会整体消费品水平，可以反映居民消费；而反映居民消费水平的要素可以包括居民实际收入和可支配收入，所以可以用其中1个指标表示，这里采用居民可支配收入这个指标。

1.3.2 投资要素

整体反映投资要素的指标是固定资产投资完成额，而固定资产投资包括中央和地方投资两项，所以再选取另一个指标——地方项目资产投资完成额。

中央投入中教育科技等投资，间接影响了人力资本的强度，从而影响到就业，这一系列的影响过程涉及很广，在接下来的模型中可以暂不考虑其影响。

市场利率是影响就业的一个很重要的指标，它可以直接影响投资情况，所以考虑将“市场利率”这个指标放入“投资”这个要素中。

1.3.3 对外贸易要素

对外贸易中的主要指标有进出口额，进出口总额，进出口差，其中进出口差最能反映对外贸易这个要素的情况，所以考虑只选取“进出口差”和“进出口总额”这个指标。

综合以上分析，得到以下影响因素指标体系：

表1 影响就业因素指标体系

1.4 样本选取

综合各数据库各指标的数据，由于年度数据样本量太小（一般从1978～2008，且1989年前缺失值严重），本文选取月度数据（2001年1月～2008年12月）作为数学模型建立的所需的统计数据。数据来源于研网。

各影响因素指标可以查询到月度数据，而根据就业的定义和数据库中数据，只能得到就业人数的年度数据。本文中利用三次样条插值法，利用2001～2008年的年度就业人数进行数据处理，得到2001年1月～2008年12月的月度数据。经过各数据整理，得到就业指标数据表如表2：

1.5 因果关系检验提取主要指标

通过以上定性的分析，我们选取了8个可能的主要因素指标，并选取了2001年1月～2008年12月的样本数据，现将对这些样本数据进行Granger因果关系检验，通过检验找到这8个指标中对就业人数影响的主要因素。

1.5.1 Granger因果关系检验原理

两个时间序列的变量在时间上有先导——滞后关系，如何考察一个变量过去的行为是否在影响另一个变量的当前行为，或者双方的过去行为在相互影响着对方的当前行为，Granger提出了一个简单的检验程序，称之为Granger因果关系检验。

对两个变量Y与X，Granger因果关系检验要求估计以下回归：

可能存在有四种检验结果：

（1）X对Y有单向影响，表现为（1）式X各滞后项前的参数整体不为零，而（2）式Y各滞后项前的参数整体为零；

（2）Y对X有单向影响，表现为（2）式Y各滞后项前的参数整体不为零，而（1）式X各滞后项前的参数整体为零；

（3）Y与X间存在双向影响，表现为Y与X各滞后项前的参数整体不为零；

（4）Y与X间不存在影响，表现为Y与X各滞后项前的参数整体为零；

Granger检验是通过受约束的F检验完成的。如针对X不是Y的Granger原因这一假设，即针对（1）式中X滞后项前的参数整体为零的假设，分别做包含与不包含X滞后项的回归，记前者的残差平方和为RSSu，后者的残差平方和为RSSR；再计算F统计量：

式中，m为X的滞后项的个数，n为样本容量，k为包含可能存在的常数项及其他变量在内的无约束回归模型的待估参考的个数。

如果计算的F值大于给定显著性水平α下F分布的相应的临界值Fα(m,n-k)，则拒绝原假设，认为X是Y的Granger原因。

1.5.2 1Granger因果检验

表2中给出了就业人数和8个指标的样本数据，对这些样本数据进行因果关系检验。

用Eviews先对就业人数和固定资产投资完成额进行因果关系检验，得到以下结果（见表3）：

表2 就业指标表

表3 就业人数与固定资产投资完成额Granger因果检验结果表

由表3F检验的相伴概率可以看出，在5%的显著性水平下，拒绝“X1不是Y的Granger原因”的假设，而不拒绝“Y不是X1的Granger原因”的假设。因此，检验结果为：固定资产投资额是就业人数的Granger原因。

同理，将就业人数与其他因素指标进行Granger因果检验，得到结果如表4：

表4 就业人数与各因素的Granger因果检验结果

综上表明以下结论：

（1）固定资产投资总额、地方项目资产投资、市场利率、居民消费价格指数和社会消费品零售总额是就业人数的Granger原因，但是就业人数不是它们的Granger原因；

（2）城镇居民可支配收入和进出口差额是就业人数的Granger原因，同时就业人数也是它们的Granger原因；

（3）进出口总额不是就业人数的Granger原因，就业人数也不是进出口总额的原因.

1.5.3 主要指标确定

以表4中的因果关系检验结论为依据，是就业人数的Granger原因的指标为影响就业人数的主要指标。则表示为如表5所示：

由上述分析可知，影响就业人数的相关因素由表5所示的7个，为了消除因素之间的多种共线性，以就业人数为因变量，表5中的影响因素为自变量，以2001年1月～2008年12月的全国月度数据为样本，建立逐步回归模型，得到以下回归结果：

表5 影响就业人数的主要指标

由此可见影响就业问题的主要因素为x1，x3，x4，x6，x7，在后续的MS-VAR模型中，本文仅考虑这5个因素的影响。

2 马尔科夫区制转移向量自回归模型的建立

2.1 马尔科夫区制转移向量自回归模型的构建

自Sims（1990）提出向量自回归模型（Vector Autoregression，VAR）以来，该方法在研究总体变量之间的关系得到广泛的应用，而马尔科夫区制转移向量自回归模型（MS-VAR）就是在向量自回归模型（VAR）模型的基础上加上马尔科夫链（Markov Chain）特性的模型。

根据上面的分析，本文采用就业人数（Y1）、固定资产投资（Y2）、市场利率（Y3）、居民消费价格指数（Y4）社会消费品零售总额（Y5）和进出口差额（Y6）构建MS-VAR模型。这些指标可以构成6维时间序列向量Yt=(Y1t、Y2t、Y3t、…Y6t）。该时

间序列在状态St可构建P阶VAR模型，如式5：

其中，St为状态变量，vtSt为常数项，它来自不同状态下的母体，Ai(St)为外生变量的系数向量。

结合经济变量常有的两状态模式，可以假设本模型存在两种状态（扩张期和收缩期），当St=1时是扩张期，当St=2时是收缩期。马尔科夫转换模型的概念主要是由两种概率分配混合产生数据，此种状态改变的现象与Chow test的观点有部分是相似的，但Chow test主张的是认为在t期的数据不是由状态一就是由状态二“独立”产生，而并非由状态一及状态二混合产生，所以马可夫转换模型会较Chow test相对来得有弹性。两状态的马尔科夫模型的状态转换矩阵可由式6加以表示：

其 中 ，0＜P11、P12、P21、P22＜1，且 P11+P12=P21+P22=1。Pij=P(St+1=j|St=i),i、j=1or2，表示状态转换的概率。本期（第t期）处于状态i而下一期（第t+1期）转换为状态j的概率为Pij。

上面叙述的状态变量St是无法观察的，且转换概率也是无法观察，但可以用最大似然估计求出在各时点t的状态概率值。

马尔科夫转换是可以用无法观察的状态变量来捕捉时间序列的数据产生过程(Data-Generating Process)。在马尔科夫状态转换模型中的参数包含常数项、平均数与误差项都会依状态的改变而有所不同，因此我们可以依照研究本身的需求，来对于某些参数进行不同状态改变的假设，来进行我们的实证分析。

2.2 马尔科夫区制转移向量自回归模型的实证分析

在进行MS-VAR模型计算之前，先要保证样本数据的平稳性，本文采用ADF检验进行，发现就业人数不是平稳序列，于是对其进行一阶差分后检验得到平稳的结论。ADF采用Eviews6进行计算，具体检验结果见表6。

表6 ADF单位根检验

表7 滞后阶数的判断

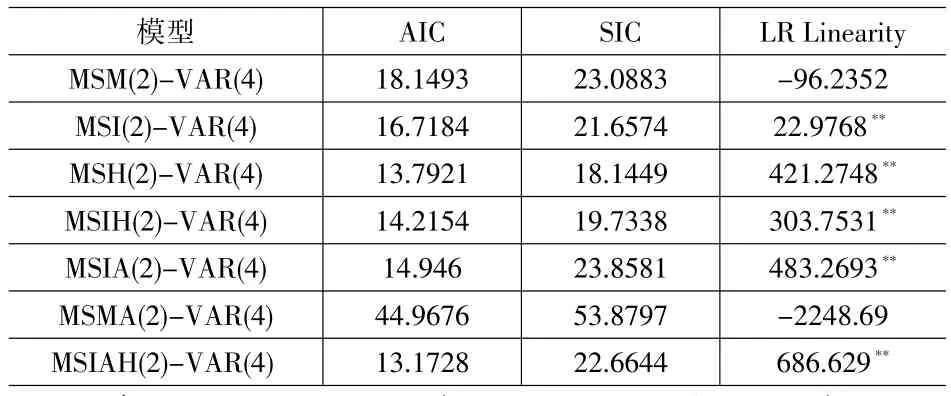
表8 最佳MS-VAR模型的选择

在对数据进行平稳化处理和平稳检验后，就可以求解模型了，本文采用OX软件包中的MSVAR优化包，采用基于极大似然估计的EM算法进行估计参数。

在进行MS-VAR分析之前，必须先确定滞后阶数(P)，本文是根据MSM-VAR模型的AIC和SIC判断准则来决定最适的滞后阶数，由表7可知，当落后期数为1的时候，AIC值为22.5177，SIC值为24.4387，在滞后期数为4时，AIC值和SIC值相对较小，代表其模型配适性最佳，因此，本文选择滞后期数为4的模型进行分析。

接下来通过AIC值、SIC值和LR Linearity值来判断MS-VAR的模式，这些值的具体大小见表8。

从表8看出，MSIAH(2)-VAR(4)模型的AIC值和SIC值最小，且其LR Linearity统计量显著，我们选择该模型来研究，对应于两种状态，截距、方差和回归系数都在发生变化。

由表9可知，当期处于状态1（扩张期），下期维持状态1（扩张期）的概率为0.9555，当期处于状态1，下期转换为状态2（收缩期）的概率为0.0445，当期为状态2，下期维持状态2的概率为0.9778，当期为状态2，下期为状态1的概率为0.0222。

由表10可知，处于状态1的平均概率为0.333，期望持续期为22.48个月；处于状态2的平均概率为0.667，期望持续期

表9 状态转换概率

表10 状态期望持续期和平均概率

为每45.02个月。可以看出，状态2的平均概率和期望持续期都大于状态1，这说明从总量上讲，2001～2008年间，我国经济的扩张期是短于收缩期的。

由于本文研究的核心是就业受其他因素的影响情况，因此文章仅提供MSIAH(2)-VAR(4)模型中就业人数增量（进行过差分处理）的参数表，由表11可知，在扩张期，就业人数的增量受到第一期到第四期就业人数增量、第二期和第三期固定资产投资、第四期利率、第三期和第四期物价指数、第一期和第二期消费总额、第一期进出口差额的显著影响；在收缩期，就业人数增量收到第一期到第三期就业人数增量、第一期到第三期物价指数、第一期消费总额的显著影响。

图1给出了每个样本观测点分别在状态1和状态2的滤子概率以及相应的平滑概率和预测概率曲线。从图1的上半部分看出，经济状态在2001年1月～2004年1月和2005年4月～2006年3月两个时段处于扩张期，从图1的下半部分看出，经济状态2004年2月～2005年3月和2006年4月～2008年12月两个时段处于收缩期。结合国家统计局发布的中国企业景气指数，该指数从2001年第一季度的118.56点上升到2004年第一季度的135.9点，成为一个明显的扩张趋势，该指数从2004年第一季度的135.9点下降到2005年第二季度的131.71点，成为一个收缩趋势，给指数从2006年第一季度的131.5点下降2008年第四季度的107点，成为一个明显的收缩趋势。从与中国企业景气指数的对比看，它与本研究得到的结论非常吻合，说明了采用MS-VAR模型对经济状态进行划分的合理性。

表11 MSIAH(2)-VAR(4)模型就业人数的参数

图1 MSIAH(2)-VAR(4)模型状态概率图

3 结论与研究展望

本研究首先采用了格兰杰因果关系检验和逐步回顾模型对影响就业的因素进行了筛选和验证，得到五个影响就业的关键因素。在此基础上，考虑到不同状态下就业与其影响因素之间的关系会有所不同，建立了MS-VAR模型。从实证的结论看，最终建立的MSIAH(2)-VAR(4)模型能够很好的区分经济状态，并给出了以下重要结论：

（1）在扩张期，就业人数的增量受到第一期到第四期就业人数增量、第二期和第三期固定资产投资、第四期利率、第三期和第四期物价指数、第一期和第二期消费总额、第一期进出口差额的显著影响；在收缩期，就业人数增量收到第一期到第三期就业人数增量、第一期到第三期物价指数、第一期消费总额的显著影响。

（2）处于扩张期的平均概率为0.333，期望持续期为22.48个月；处于收缩期的平均概率为0.667，期望持续期为45.02个月。

后续研究中，我们将考虑状态的持续性，研究是否某一状态持续的时间越长，其转换为另一状态的概率越大的期间相依现象。同时，将考虑加入误差修正模型对MS-VAR模型进行拓展，研究就业的长期均衡和短期突变现象，为就业问题提供更多的决策依据。

[1]Martine Carre,David Drouot.Pace Versus Type the Effect of Economic Growth on Unemployment and Wage Pattern[J].Review of Economics Dynamics,2004,（7）.

[2]刘新卫.就业增长率与经济增长率关系的预测模型[J].科技创业，2008，(12).

[3]Pissarides Chirstopher A.Equilibirum Unemployment Theory[M].Cambridge：MIT Press，2000.

[4]何静慧.经济增长、技术进步与就业的关系——以浙江为例[J].统计与决策 ，2005，(10).

[5]张晓旭.中国就业增长与产业结构变迁关系的考量[J].统计与决策,2007，(24).

[6]李晓嘉，刘鹏.我国产业结构调整对就业增长的影响[J].山西财经大学学报，2006，(1).

[7]吴小松，范金，胡汉辉.我国就业增长与结构变迁的影响因素：基于SDA的分析[J].经济科学，2007，(1).

[8]冉光和，曹跃群.资本投入、技术进步与就业促进[J].数量经济技术经济研究，2007 ，(2).

[9]Hamilton,James D.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle[J].Econometrica,1989，（57）.