基于二阶段抽样的双重抽样框估计量设计

贺建风

（仲恺农业工程学院 统计系，广州 510225）

0 引言

传统抽样调查设计及其估计理论一般基于单一抽样框的假定。然而，随着社会经济的飞速发展，城市化进程的推进与产业政策的转移使得人口流动与生产单位转移变得比以往任何时期都要频繁，很难建立覆盖所有目标单位的单一抽样框，有时即使可以建成，建设费用也一定是高昂的，或者需要很长的时间才能完成，建成后还得耗费大量资源对其进行不断地更新与维护，这不符合抽样调查成本低、时效性强的原则。有一种方法可以弥补单一抽样框覆盖不完全问题，那就是采用双重抽样框（即两个相互独立的抽样框），使他们联合起来能够完全覆盖目标总体，当然这些抽样框应该是现有的资料，或者能够轻易构建起来，使提高调查精度的同时还可以节约调查的固定成本。

国外对于双重抽样框的理论研究起源于上世纪60年代。Hartley(1962，1974)对双重抽样框的估计问题进行了开创性研究[1]，随后 Fuller and Burmeister(1972)，Bankier(1986)，Kalton and Anderson(1986)等人在此基础上对双重抽样框的估计问题进行了拓展[2][3]，但是这些研究仅局限于单一阶段抽样，对于在双重抽样框抽样情形下的二阶段抽样估计量研究的甚少，其中Casady,Snowden,and Sirken（1981）将Hartley 提出的基于双重抽样框的估计方法应用于电话名录框与区域框组合抽样设计的分层多阶段抽样[4]，B.C.Saxena,P.Narain,A.K.Srivastava（1984）探讨了双重抽样框下的二阶段抽样估计问题，但是只考虑了次级抽样单元在各域的单位调查成本相同的情形[5]。在国内，由于行政分级的政治模式，多阶段抽样调查成为实际中应用较广泛的一种调查手段（尤其是政府调查项目）。国内理论界对于多阶段抽样的研究仅局限于单一抽样框的前提，对于双重抽样框的情形未曾涉及。基于此，本文拟引进国外相对丰富的双重抽样框估计理论，研究国内目前流行的多阶段抽样调查，将多阶段抽样扩展到双重抽样框的情形，以求弥补国内在这一领域的空缺。为了分析问题的简便及计算的简单可行，本文仅对双重抽样框下的二阶段抽样调查进行研究，对于更多阶段的抽样调查情形可以按照本文的思路进行推广。

1 符号及含义

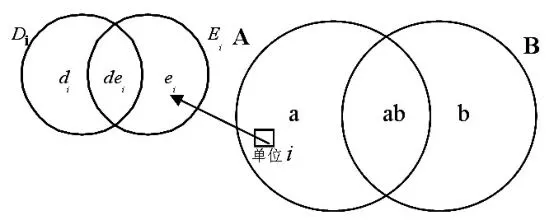
图1 双重抽样框的一般结构

在二阶段的抽样中，假定每个阶段都面临着从双重框中抽选调查单元。设第一阶段抽样有两个存在相互重叠部分的抽样框A与B共同组成目标总体，并记NA与NB分别为抽样框A与B中的总体单位个数，nA与nB为独立取自抽样框A与B的样本数。从总体中抽取的初级抽样单元能够被分入三个子域（见图1），即域a，域b和域ab。

域a：包含来自于抽样框A而不在抽样框B中的总体单位，记Na为总体单元个数；

域b：包含来自于抽样框B而不在抽样框A中的总体单位，记Nb为总体单元个数；

域ab：包含来自于抽样框A与B公共部分的总体单位，记Nab为总体单元个数。

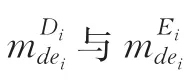
2 总体总值估计量

Hartley's(1962)提出简单随机抽样情形下的总体总量事后分层估计量：

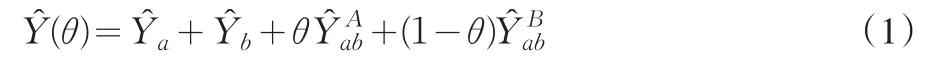
其中是域a的总体总值估计量，是域b的总体总值估计量，是域ab中来自A抽样框的总体总值估计量，是域ab中来自B抽样框的总体总值估计量，θ为抽样权重系数，且0≤θ≤1。

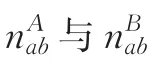
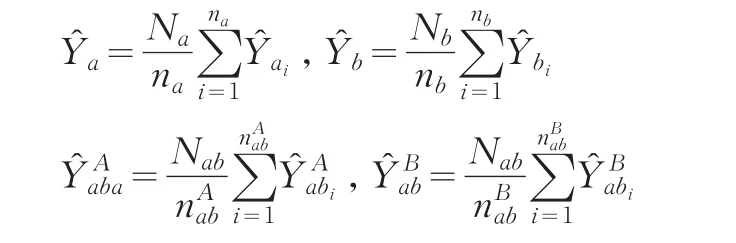
类似（1）式，第i个初级抽样单元的总体总量事后分层估计量为：

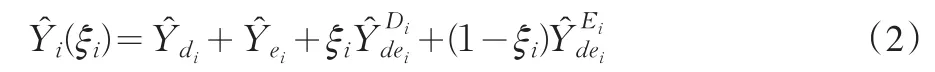
将（2）式代入第一阶抽样下各子域的总体总值估计量公式中，再代入式（1）可得：

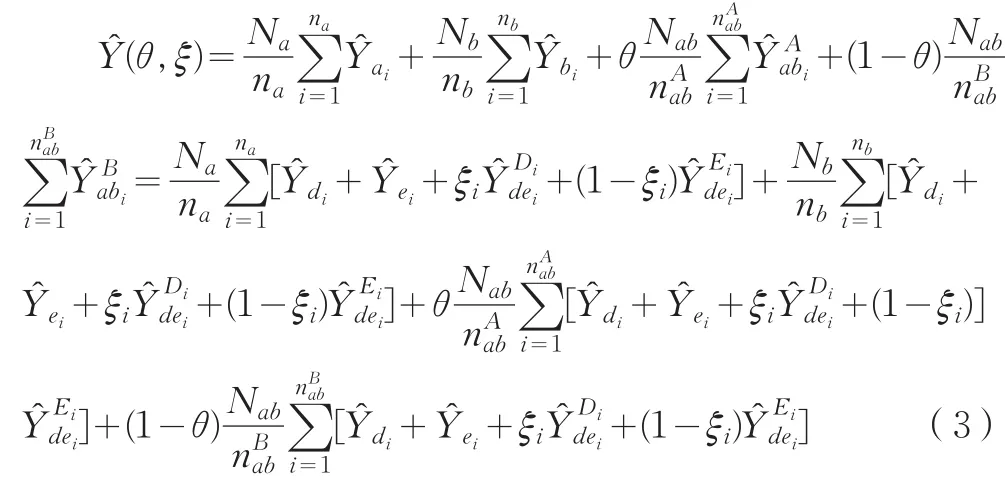
3 总值估计量方差和方差的无偏估计

由于从两个抽样框选取样本是相互独立的，所以来自A抽样框的统计量与来自B抽样框的统计量之间的协方差为0，即：

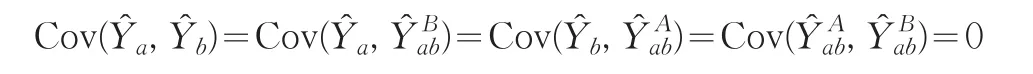
所以（1）式中总体总值估计量的方差可以表示为：

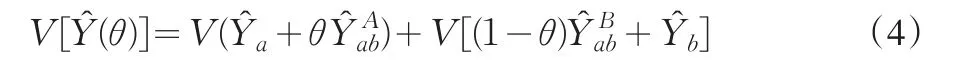
对于每个抽样框的两个子域进行事后分层，估计量的方差接近于：

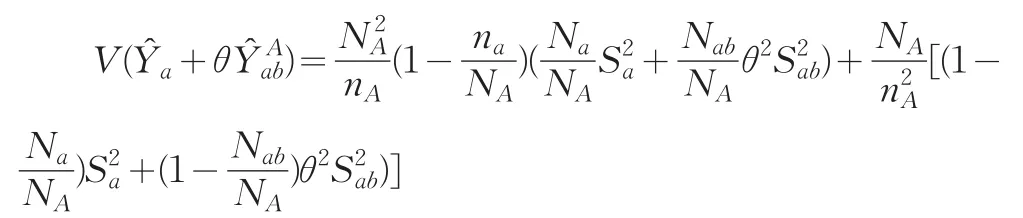
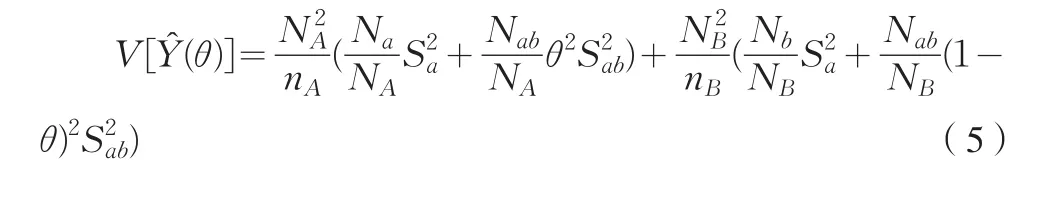
根据式（5）估计量(θ)的方差，利用二阶段抽样的估计量方差公式可以推出（3）式估计量(θ,ξ)的方差为：

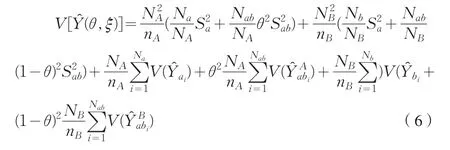
接下来，可以给出估计量方差的无偏估计，其具体形式如（8）式：

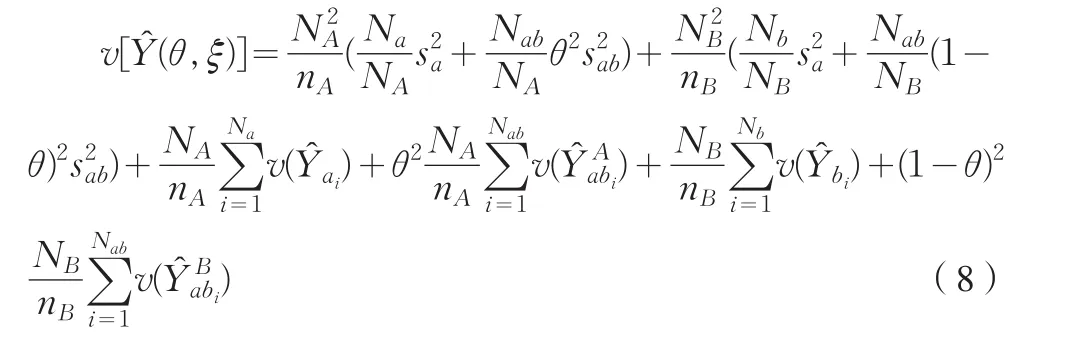
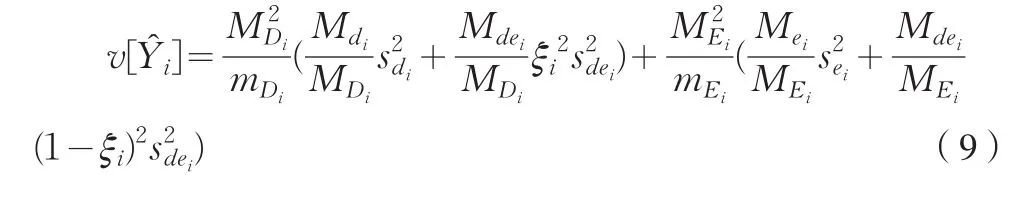
4 结束语

本文打破了传统抽样调查仅基于单一抽样框分析的束缚，引进了在实际中成本更低廉、覆盖面更广的多重抽样框调查新思路；针对双重抽样框下的二阶段抽样估计理论进行了研究，给出了总体总值估计量及其估计量方差，并给出了方差的无偏估计。本文的重要意义在于为二阶段抽样中采用双重抽样框提供理论支持。

本文的研究展望有如下几点：其一，本文的研究仅基于所有阶段以及各抽样框的调查均为简单随机抽样的情形，更进一步的研究需要将这一估计方法拓展到一般类型抽样调查的场合；其二，对于多重抽样框以及多阶段的情形本文并未展开分析，感兴趣的读者可以在本文的基础上进行拓展，但估计量的计算将更为繁琐；其三，本文考虑的是二个阶段均为双重抽样框的情形，并且假定所有双重抽样框的结构均为图1所示，对于某阶段为单一抽样框以及双重抽样框的结构为完全重叠或某抽样框包含另一个的情形而言，其估计量的计算比本文更简单。限于篇幅，这里不再赘述。

[1]Hartley H.O.Multiple Frame Surveys[C].In Proceedings of the Social Statistical Section,ASA,1962.

[2]Hartley,H.O.Multiple-Frame Methodology and Selected Applications[J].Sankhya,Ser.C,1974，（36）.

[3]Fuller,W.A.,Burmeister,L.F.Estimators for Samples Selected from Two Overlapping Frames[C].In Proceedings of the Social Statistics Section,American Statistical Association,1972.

[4]Casady,R.,Snowden,C.,Sirken,M.A Study of Dual Frame Estimators for the National Health Interview Survey[C].Proceeding of the Survey Research Methods Section,American Statistical Association,1981.

[5]B.C.Saxena,P.Narain,A.K.Srivastava.Multiple Frame Surveys in Two Stage Sampling[J].The Indian Journal of Statistics，1984，(4).