实时动态差分法测量精度模型及实验研究＊

董春来，史建青，郭淑艳

（1.中国矿业大学，江苏徐州221008；2.淮海工学院，江苏 连云港222005）

0 引 言

实时动态差分法（RTK），是一种新的常用的GPS测量方法。GPS RTK技术有作业效率高、作业自动化、集成化程度高、作业条件要求低、操作简便、容易使用、数据处理能力强等优点，具有很强的应用性，广泛应用于测绘的各个行业，如：工程放样、地形测图、勘测设计，土地勘界、地籍测量、房产测绘、地质探矿等领域[1]。RTK技术测量精度一直是测绘专家与学者关注的焦点问题，普遍研讨RTK测量误差因素及提高对策，取得许多可信的实用性成果[2－3]。本文旨在不追求提高RTK测量精度的方法与措施，而在于通过分析RTK测量精度的实际表现结果，运用曲线回归分析方法，探究RTK测量精度的数学模型，简便、快捷求解某种仪器RTK测量精度，实时预测评价实现控制测量等级精度可行性。

1 RTK测量精度的特征分析与算法模型

1.1 RTK测量的工作方式

RTK定位技术就是基于载波相位观测值的实时动态定位技术，是GPS测量技术与数据传输技术相结合而构成的组合系统。RTK GPS测量系统主要由GPS接收机、数据传输系统、软件系统部分组成。它的工作原理是：使用至少2台同时工作的GPS接收机（1台基准站，1台流动站），利用载波相位差分技术实时处理2个测站载波相位观测量的差分进行测量。基准站通过数据链将其观测值和测站坐标信息一起传送给流动站，流动站不仅通过数据链接收来自基准站的数据，还要采集GPS观测数据，并在系统内组成差分观测值进行实时处理，得出移动站实时定位结果[4]。

1.2 RTK测量误差特性分析

根据上述RTK测量工作原理，参考相关研究文献表明[5－7]，RTK测量精度与基准站位置选择、坐标转换参数选定、观测时间选取、仪器设备特性等多方面有关，有着显著特点。

1）RTK测量精度各要素影响最终体现在基准站与移动站的基线解算精度的高低，转换参数选定、设备选取及卫星状况等有着系统性影响。

2）RTK测量误差与两站（基准站与流动站）间距有直接关系，间距小精度高，间距大精度低。

3）RTK测量误差与两站间距大小成非线性关系，间距在有限范围内，精度变化不大；间距超过此范围，距离越远，精度降低越快。

1.3 RTK测量精度的数学模型

根据RTK测量误差的特性分析，反演比对数学函数，认为以指数函数为基础拟合RTK测量的基线距离相对误差，具有良好的相关性，能合理反映RTK测量精度。

设以RTK测量基线距离（x）为X轴，以坐标反算距离与测量距离之差值Δx的相对误差（y＝Δx／x）为Y 轴，则有：

令v＝lny，A＝lna，则有

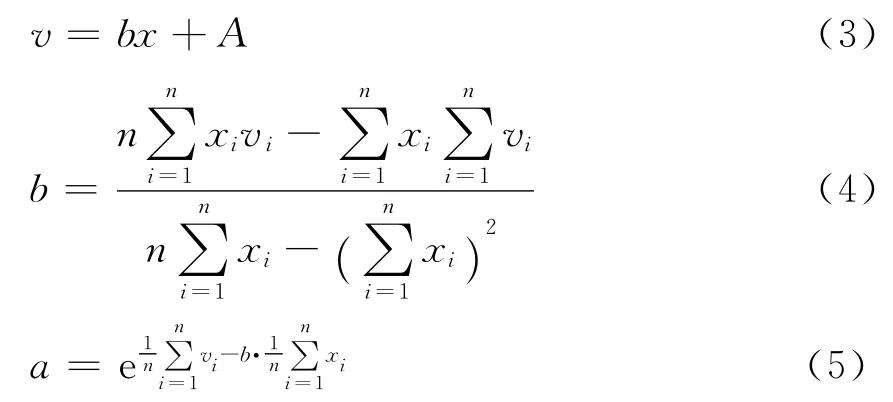
可见，通过最小二乘原理，就可求解模型参数a和b.

于是可得相对精度预测评价的数学模型式（1）。其相对误差中误差m为

可见，RTK基线边相对测量精度评价的数学模型为

2 RTK测量精度的实验分析

2.1 实验概述

某线路长近100km，在工程控制测量中，选择了GPS静态、动态及全站仪的组合测量方式，全线布设了6个C级GPS静态网点，实现整个线路首级控制测量，为了有意识检测分析GPSRTK测量定位精度，在次级控制测量中，采用NOVATEL（5 mm＋1ppm＊D）和R－202N（2mm＋2ppm＊D）联合进行，取得了满意的控制成果。

在数据成果处理过程中，对测点的精度与距离的关系进行作图分析，以RTK基准站与移动站距离为X轴，以动态所测的点间相对误差为Y轴，用CASS中展点作图，如图1，从该图中散点的分布来看，点的精度与距离之间并非呈现一般的线性关系。可以看出，当流动站距基准站的距离在6km之内，所测点距离相对误差变化不大，超过6km时，所测点的精度便逐渐下降，当流动站距基准站的距离超过12km时，所测点的精度下降较快。

2.2 拟合分析

根据实际观测数据，利用数学模型式（1）、（6），考虑式（4）与式（5），选取131个有效点进行解算得RTK测量精度计算经验公式为

y＝0.000006819e0.00009488x±8.689E－6（8）

对应此数学模型绘制拟合曲线与测点关系如图2，由图看出，曲线与点图吻合较好，体现曲线与测点相对误差的一致性。

比对城市测量规范，RTK测量精度在一定范围内满足相应等级测量要求，如表1，实验表明，指数曲线能较好的反映RTK测量精度，在距离15 km以内，曲线很好反映RTK测量精度，随着基准站与移动站距离的进一步增加，测量精度加速降低，曲线拟合度下降。

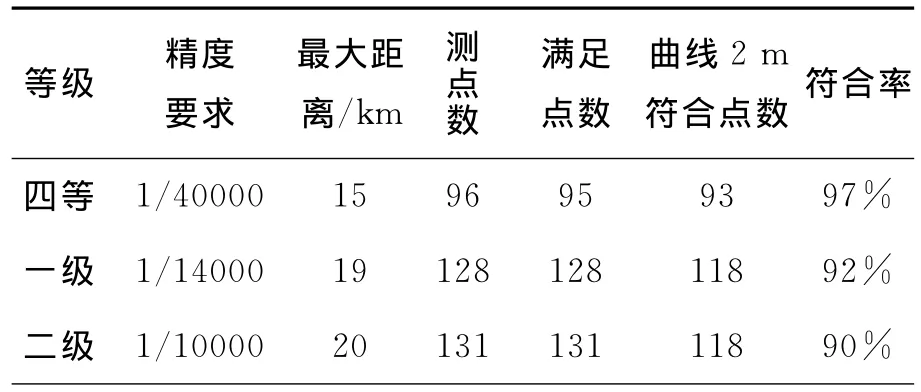
表1 RTK测量满足精度及曲线拟合度表

3 结 论

1）影响RTK测量精度的因素很多，在环境良好的情况下，RTK测量精度主要决定于基准站与移动站之间的距离[8]。

2）运用指数函数模型能良好地体现RTK测量精度，在一定距离范围内，较好反映RTK测量精度指标，距离较大（大于19km），曲线拟合度明显下降，不能反映RTK测量精度。

3）实验表明，环境条件良好，距离小于15km范围，利用RTK技术能达到四等光电导线测量精度要求；距离较大（大于20km），利用RTK技术难以实施城市控制测量。

4）取得的数学模型适用于良好外界条件下的特定仪器设备，对于其它类型的仪器设备，可以据此简单实验，求出相应参数a与b，求得定量反映该仪器RTK测量精度的实用公式，指导测量实践。

5）曲线拟合选取较为简单实用的指数函数模型，若要提高曲线拟合度，可以选取多项式、双曲线等复杂函数实施拟合。

[1]余小龙，胡学奎.GPSRTK技术的优缺点及发展前景[J].测绘通报，2007（10）：39－42.

[2]黑志坚，周秋生，曲建光，等.GPSRTK测量成果的精度估计及应用探讨[J].哈尔滨工业大学学报，2006，38（8）：1295－1298.

[3]周 立.GPS RTK流动站误差影响分析与对策[J].测绘通报，2006（6）：31－33.

[4]于小平，杨国东，许惠平，等.GPSRTK高程拟合方法精度研究[J].测绘通报，2006（11）：19－21.

[5]张振军，谢中华，冯传勇.RTK测量精度评定方法研究[J].测绘通报，2007（1）：26－28.

[6]段祝庚，赵建华.用RTK进行带状地形图根控制测量的精度[J].中南林业科技大学学报，2007，27（6）：122－126.

[7]周晓华，李永兴，吴根姣，等.RTK技术在控制测量中的应用探讨[J].测绘通报，2007（7）：41－43.

[8]柯福阳，王 庆，潘树国，等.GNSS网络RTK算法模型及测试分析[J].东南大学学报·自然科学版，2009，39（4）：763－768.