基于多层模糊Petri网的编队空战战术决策

孙体忠， 孙金标

(空军指挥学院，a.研究生大队; b.科研部，北京 100097)

0 引言

编队空战是现代空战的主要形式，也是未来空战的发展趋势，它与单机空战相比，最显著的差别在于多机之间的战术协同。编队空战战术决策过程中，编队指挥员面临巨大的决策压力，其不仅要准确把握战场态势变化，还要能够根据空战进程和态势变化迅速调整编队攻防战术，同时确保对编队指挥控制的连续性。为减轻编队指挥员的决策压力，提高决策效率，机载战术辅助决策系统已成为研制新一代战机的迫切需求。当前，对编队空战战术决策问题的研究主要集中于复杂系统理论［1］和现代智能技术［2］，但在实际应用中始终面临由于决策因素多而导致系统复杂性增强，以及系统的非结构性导致决策推理复杂的现实问题［3］。

模糊Petri网(Fuzzy Petri Net，FPN)是一种用网状图形表示系统建模的方法，它能以网图的形式简洁地表示系统中的并行、同步、冲突和因果等关系，易于通过构造的模型来分析系统的性能，已被应用于故障诊断［4］和误差评估［5］、智能决策［6－7］等方面，并取得了很好的效果。文献［8］提出利用FPN建模实现超视距空战战术的模糊推理决策。模糊Petri网(FPN)发挥了模糊推理和Petri网的优点，能够很好地利用先验知识和专家知识进行多准则推理，推理不仅具有直观形象的优点，而且也使得推理的实时性得以实现［9］。但FPN存在不能适应知识库扩展和更新的问题，以及存在不能利用面向对象和结构化方法对复杂知识库进行建模的不足。因此，针对编队空战战术决策问题，使用多层模糊 Petri网(Hierarchical Fuzzy Petri Net，HFPN)方法对知识库进行建模，通过利用抽象库所和抽象变迁的结构化方法来提高模型对复杂知识的表示能力，以降低编队空战战术决策的复杂性。

1 多层模糊Petri网(HFPN)

1.1 基于HFPN的知识库建模过程

复杂决策知识分析和HFPN的建模过程是一个逐渐增补和反复完善的过程。参考文献［6］，HFPN建模的主要步骤如下:1)分析决策系统并确定决策系统的层次关系;2)创建初始HFPN，初始HFPN是一个最高层次的抽象系统，系统状态和行为分别由抽象的库所和变迁表示;3)分析决策知识，建立规则库;4)将抽象的库所和变迁逐步精细化为协调一致的FPN，并集成所有的子网，调整模型的总体结构，检查知识库行为;5)检查、完善模型，当模型达到要求，知识库的建模过程结束，否则转至第4)步;6)模型简化，为了简化计算，用模块合并方法和“补弧”运算对模型进行简化，“补弧”连接输入库所和变迁，表示逻辑“非”回路。

1.2 推理算法

FPN的结构可用八元组来表示:FPN=(P，R，I，O，H，θ，γ，C)。其中:P={p1，p2，…，pn}是一个有限库所集合;R={r1，r2，…，rm}表示变迁集合;I:P×R→{0，1}为n×m输入矩阵，表示库所与规则之间的映射关系，当 pi到 ri之间存在有向弧时，I(pi，rj)=1(i=1，2，…，n)(j=1，2，…，m)，当 pi到 ri之间不存在有向弧时，I(pi，rj)=0;O:P ×R→{0，1}为 n×m 输出矩阵，表示规则与库所之间的映射关系，当ri到pi之间存在有向弧时，O(pi，rj)=1，当rj到pi之间不存在有向弧时，O(pi，rj)=0;H:P × R→{0，1}为 n × m 矩阵，表示从库所到规则的补弧集合;θ:P→{0，1}为P可信度向量，它表示P与［0，1］间实数的映射，初始可信度向量记作θ0;γ:P→{0，1}为库所中托肯的标识向量，它表示P中托肯的状况，初始标识向量记作γ0;C=diag{c1，c2，…，cm}，cj(j=1，2，…，m)为规则 rj的可信度。

2 基于HFPN的编队空战战术决策模型

2.1 编队空战战术决策的初始HPFN结构

一般情况下，空战从迎头超视距开始，随着距离的接近，战机可能已进入视距内空战，也可能正处于超视距向视距内的转换阶段。特别是现代中距弹和近距弹在射程上有交叉的现象，使得某一态势下战机既可使用超视距空战战术也可使用视距内空战战术，所以每当空战开始或空战态势发生变化时，编队指挥员就要对进入哪种空战样式进行选择。当选择进入超视距空战或视距内空战样式后，编队指挥员要根据空战态势确定当前是组织进攻还是组织防御，即对编队战术意图进行决策;空战样式和战术意图确定后，编队指挥员进一步根据敌我相对态势和攻击状态对编队使用什么战术进行决策;当选择进入超视距转视距内空战样式后，编队战术意图即为接近敌机，此时编队指挥员直接对使用什么样的转换战术进行决策;若威胁较大或其他原因需要退出战斗则指挥编队退出战斗。

根据上述对编队空战战术决策过程的分析，基于HFPN的建模思想，定义编队空战战术决策HFPN中的抽象输入(输出)库所和抽象变迁，见表1，并对抽象库所和抽象变迁之间的层次化结构关系进行分析，建立编队空战战术决策的初始HFPN结构，如图1所示。该初始HFPN结构由3个层次共8个子模块组成:第1层为编队空战样式决策层，即为空战样式决策子模块(Mode1);第2层为编队空战战术意图决策层，包括超视距和视距内战术意图决策子模块(Mode2，Mode3);第3层为编队战术决策层，包括超视距攻击/防御反击战术决策子模块(Mode4/Mode5)、超视距转视距内战术决策子模块(Mode6)和视距内攻击/防御反击战术决策子模块(Mode7/Mode8)。

表1 HFPN中的抽象库所和抽象变迁Table 1 Abstract places and abstract transitions in HFPN

图1 编队战术决策的初始HFPN模型Fig.1 Initial HFPN model of tactical formation decision-making

2.2 编队空战战术决策规则的提取

编队空战战术决策规则采用“if…then”的表达式，决策规则的提取步骤如下:1)根据战术理论和专家经验选取决策控制变量并确定其隶属函数;2)确定模糊语言变量的取值;3)分析决策结果;4)提取战术决策规则并给出规则的可信度。

影响战术决策的控制变量由许多定量指标和定性指标共同组成。确定控制变量的模糊隶属函数时:对于越大越好的指标，其隶属函数采用F分布中岭形分布的偏大型;对于越小越好的指标，其隶属函数采用F分布中岭形分布的偏小型;对于要求介于某一区间的指标，其隶属函数采用F分布中正态分布的中间型。

3 基于HFPN的“二对一”空战战术决策实例验证

编队空战通常以四机和双机为战术编队，而四机编队在空战过程中又将分为两个双机编队，所以，编队空战战术决策的研究重点是双机编队战术决策问题。双机编队空战包括“二对二”和“二对一”两种形式，但实际空战中“二对二”空战在战术应用中仍然以“二对一”空战战术为主。在此，将以典型的“二对一”空战战术决策为例，对基于HFPN的战术决策建模方法进行验证。

3.1 “二对一”空战战术规则库

针对表1中的8个抽象变迁即决策规则库R1～R8，通过分析“二对一”空战战术决策知识，经过选取决策控制变量、确定隶属函数、确定模糊语言变量和确定决策结果属性等环节，依据2.2节方法和步骤提取决策规则并建立相应的规则库。由于篇幅的限制，在此不对规则库中的详细规则进行赘述，仅列出各规则库对应的规则数量、控制变量和决策结果属性，见表2。

表2 决策控制变量和决策结果Table 2 Control variables and results of tactical decision-making

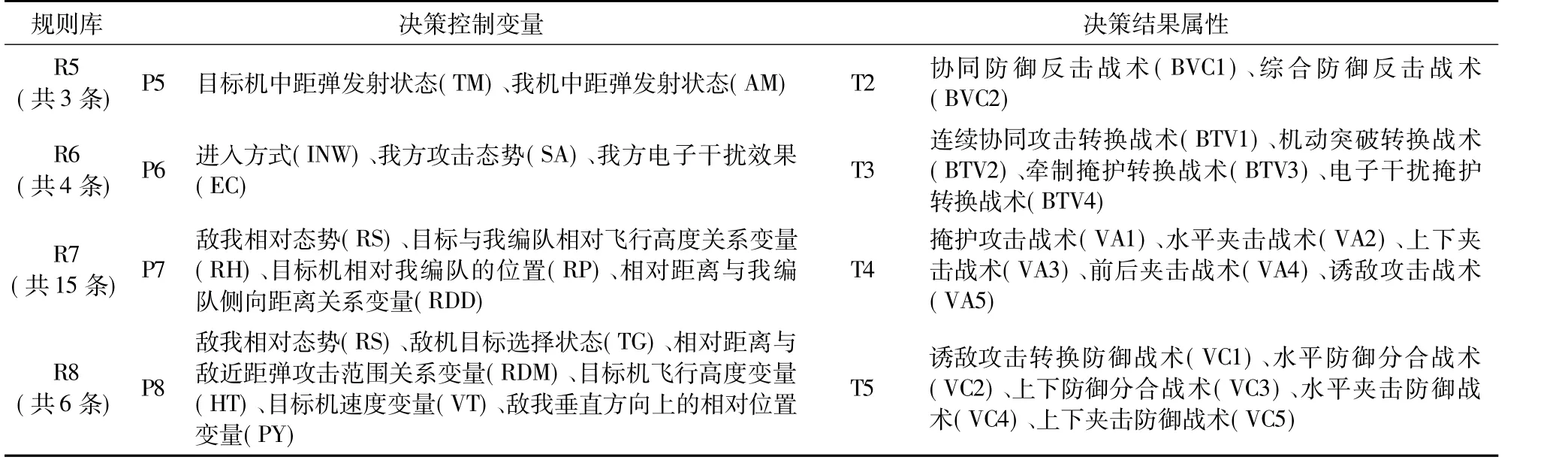
(续表2)

3.2 “二对一”空战战术决策的HFPN模型

在“二对一”规则库建立的基础上，通过上述决策控制变量和决策结果属性分别将2.1节中的8个抽象库所和8个抽象变迁逐步精细化为协调一致的决策子FPN。参考1.1节中HFPN的建模过程和步骤，经过集成所有的子FPN网、调整模型的总体结构、模块合并、“补弧”运算以及对模型进行简化等建模步骤，建立“二对一”空战战术决策HFPN结构，如图2所示。

图2 “二对一”编队战术决策的精细化HFPN模型Fig.2 Refined HFPN model of 2:1 tactical formation decision-making

从图2可以看出:经过合并和精细化处理后的HFPN模型共有93个库所和71个变迁。其中，62个纯输入库所对应模糊控制变量，7个输入输出库所对应空战样式决策结果和战术意图决策结果。24个纯输出库所对应“二对一”空战的编队协同战术;71个变迁对应71条决策规则。

3.3 算例

态势:我方Su－27B双机编队与敌F－16C单机进行空战，我双机编成横队队形，挂载中距空空导弹和近距空空导弹，飞行高度5500 m、速度255 m/s，敌机飞行高度5000 m、速度240 m/s，我长机方位角55°、进入角－55°，僚机方位角 80°、进入角 －20°，长机与敌机相距35 km，僚机与敌机相距40 km，形成迎头态势，双方均未进入近距弹攻击范围;我长机雷达处于跟踪状态而未发射中距弹，敌机雷达处于单目标扫描状态。

通过Matlab编程实现基于HFPN的“二对一”空战战术决策，决策结果为:第1层输出中，{p18，p24，p29，p30}={0.9，0.0，0.0，0.0}，输出最大值 p18=0.9，即表明选择超视距空战样式;第2层输出中，{p45，p50，p60，p66}={0.81，0.0，0.0，0.0}，即选择超视距攻击的战术意图;第 3 层输出中，{…，p75，p76，p77，p78，p79，p80，p81，…}={…，0.1022，0.0，0.729，0.0，0.0，0.0，0.006，…}，最大值为p77=0.729，所以最终决策结果选择超视距攻击战术中的垂直夹击战术。

此外，选取各种空战样式下的10组空战态势数据进行验证，分析10组态势数据所输出的决策结果表明:各种态势下的决策结果符合“二对一”空战的战术应用规律，说明基于HFPN的编队空战战术决策方法能够对编队空战战术进行有效的模糊推理决策。

4 结论

对于编队空战战术决策问题，基于FPN的建模方法以网图的形式直观地表示了具有非结构化特征的空战战术决策问题，但FPN不能利用面向对象和结构化方法对复杂知识库进行建模。为此，提出基于HFPN的建模方法，在对编队空战战术决策过程的层次化结构进行分析的基础上，利用抽象库所和抽象变迁建立了编队空战战术决策的初始HFPN模型。之后，以典型“二对一”空战战术决策为例进行实验验证表明:基于HFPN的建模方法对编队空战战术决策系统进行建模，不仅可以发挥模糊Petri网基于知识的表达和逻辑推理功能，而且降低了编队空战战术决策的复杂性。

［1］ 杨镜宇.分布式智能决策问题研究［D］.北京:空军指挥学院，2002.

［2］ 钟麟，佟明安，钟卫，等.基于粗糙集－神经网络编队协同空战决策系统［J］.火力指挥与控制，2008，32(5):64-66.

［3］ 丁全心.现代空战中的战术辅助决策技术［J］.电光与控制，2009，16(12):1-4.

［4］ 戎梅，赵廷第，郭江杰.模糊Petri网在航天发射系统故障诊断中的应用研究［J］.航天控制，2009，27(4):82-87.

［5］ LUO X，KEZUNOVIC M.Implementing fuzzy reasoning Petri-Nets for fault section estimation［J］.IEEE Transactions on Power Delivery，2008，23(2):676-685.

［6］ 伊洪冰，张春润，刘增勇，等.模糊Petri网在装备保障指挥决策中的应用研究［J］.指挥控制与仿真，2008，30(4):99-102.

［7］ DONG Zhuoning，ZHANG Rulin，CHEN Zongji.Intelligent decision-making for hazardous weather avoidance based on hierarchical fuzzy Petri nets［J］.Journal of System Simulation，2008，20(19):5147-5151.

［8］ 史志富，张安，刘海燕，等.基于模糊Petri网的空战战术决策研究［J］.系统仿真学报，2007，19(1):63-66.

［9］ 孙体忠，孙金标.空战战术双层决策模型设计［J］.电光与控制，2011，18(4):37-40，96.