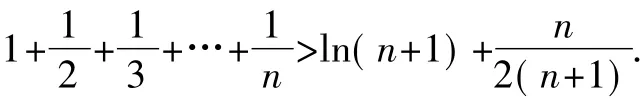一个重要函数不等式≤ln(1+x)≤x及其应用

430074 武汉市洪山高级中学 张 顺 戴 露

(Ⅰ)当n=2时，求函数f(x)的极值;

(Ⅱ)当a=1时，证明：对任意的正整数n，当x≥2时，有 f(x)≤x-1.

解 (Ⅰ)由已知得函数f(x)的定义域为{x|x＞1}，

(1)当 a＞0 时，由 f'(x)=0，得

当 x∈(1，x1)时，f'(x)＜0，f(x)单调递减;

当 x∈(x1+∞)时，f'(x)＞0，f(x)单调递增.

(2)当a≤0时，f'(x)＜0恒成立，所以f(x)无极值.

当a≤0时，f(x)无极值.

要证f(x)≤x-1

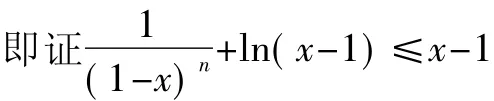
而ln(x-1)=ln(x-2+1)≤x-2

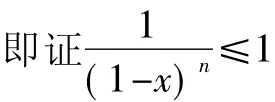
而x≥2可得1-x≤-1

综上，所以原不等式成立.

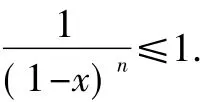
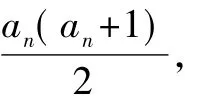
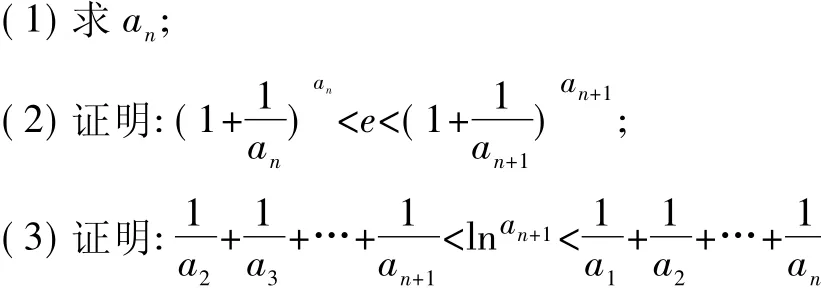
解 (1)由Sn-Sn-1=an易得通项公式为an=n.

点评 本题的第二问第三问均是应用不等式的变形得到.

(Ⅰ)用 a表示出 b，c;

(Ⅱ)若 f(x)＞lnx在［1，+∞］上恒成立，求 a的取值范围;

解 (Ⅰ)可求出b=a-1，c=1-2a.

f(x)＞lnx，故f(x)≥lnx在1，+[)∞上恒不成立.

∴ f(x)≥lnx，

故 f(x)≥lnx，在［1，+∞)上恒成立.

将上述n个不等式依次相加得

整理得