基于小波包变换与前向线性预测滤波的光纤陀螺去噪算法

申 冲 陈熙源

(东南大学仪器科学与工程学院，南京 210096)

(东南大学微惯性仪表与先进导航技术教育部重点实验室，南京 210096)

光纤陀螺是20世纪70年代发展起来的一种新型惯性仪器［1］.作为惯导系统的核心元件，光纤陀螺的输出精度直接影响着惯导系统的性能.由于光纤陀螺易受环境噪声的影响，因此在陀螺信号中除有用信号之外，还往往伴有大量的噪声，相对微弱的信号通常会淹没在强噪声中，因此如何减小噪声对陀螺信号的影响便成为亟需解决的问题［2］.

小波分析是传统的去噪方法，已广泛应用到陀螺及其他信号的去噪处理中［3-5］，并取得了良好的效果.作为小波分析方法的改进，小波包变换也被应用到光纤陀螺信号去噪中，由于小波包能对信号进行更细致的分解，从而得到了优于小波分析的去噪结果［6］.此外，FLP 算法［7］、LMS 算法［8］等也在光纤陀螺信号去噪中得到了广泛应用.目前已有的方法基本上是利用单一算法对光纤陀螺信号进行处理，去噪精度有限.

本文针对光纤陀螺信号的噪声，提出了一种基于小波包变换与FLP算法的去噪方法——WPTFLP算法.该算法结合小波包与FLP算法的优点，充分利用小波包变换在信号多尺度分解以及FLP算法高精度去噪的优势，在仅增加较低复杂度的基础上，有效地减小了噪声对光纤陀螺输出的影响，从而提高了光纤陀螺的精度与惯导系统的性能.

1 小波包变换原理

在正交小波变换中，多尺度分解只在A空间进行，而没有在D空间内进行进一步分解，即C0=A1⊕D1=A2⊕D2⊕D1=…，其分解具有一定的局限性.小波包变换则提供了更为灵活的分解方式，将频带进行多层次划分，对小波分解中没有细分的高频段进一步分解，并能够根据被分析信号的特征，自适应地选择相应频带，使之与信号的频谱相匹配.小波与小波包变换如图1所示［9］.

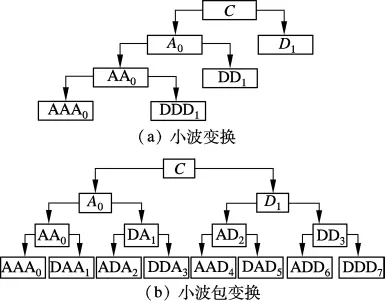
图1 小波分解与小波包分解对比图

按照不同的尺度因子，多分辨率分析把Hillbert空间分解为所有子空间的正交和.为进一步对小波子空间Dj进行频率的细分，可将尺度空间Aj和Dj用一个新的子空间统一起来表示.若令，则Hillbert空间的正交分解可用的分解统一为

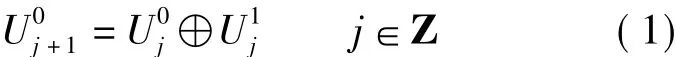
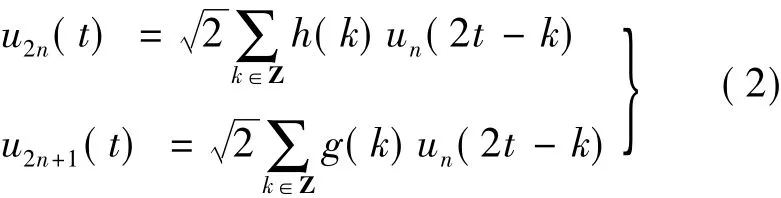
式中，g(k)=(－1)kh(1－k)，即2系数也具有正交关系.当n=0时，式(2)可以直接给出:

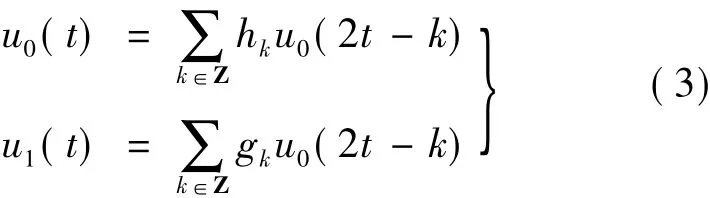
式中，u0(t)和u1(t)分别为尺度函数和母小波函数，即小波包是基于小波变换的进一步发展，能得到更精细的分解结果.

2 FLP去噪原理

FLP滤波即前向线性预测滤波，其思路是把先前的信号乘以相应的权重来预测当前时刻的信号，其最佳权重的获取需要一个迭代过程.此过程首先设定权重初始值为零，然后使用最小均方差理论来最小化当前时刻的信号与预测值之间的差值，不断更新从而最终获得一个稳定收敛的权重值.

当前时刻陀螺信号的估计值为

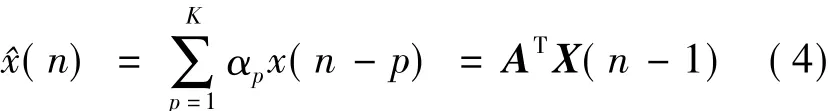
式中，X(n－1)={x(n－1)，x(n－2)，…，x(n－K)}T为先前时刻陀螺输出所组成的向量，x(np)为先前时刻的陀螺信号;A为预测滤波器的权重系数矢量;αp为权重;K为阶数.其中K的选取为影响该算法应用的重要因素之一，阶数越大，去噪效果越好，但会加大去噪过程的计算量并影响去噪过程的实时性.经过多次反复试验，选取K=60作为本文中FLP滤波器的阶数.

根据最小均方误差准则，FLP的均方误差即损失函数可定义为

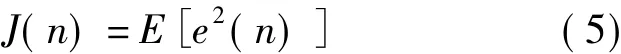
式中，e(n)=x(n)－^x(n)，表示FLP误差.根据最小均方差准则来最小化前向线性预测误差，即要选择合适的权重以使评价函数取得极小值.由最小均方值可得权重的迭代调整公式为［7］

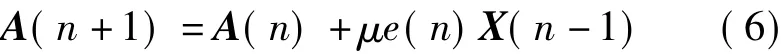
式中，μ为一个正的常量，用以控制整个迭代过程的收敛速度.μ取值较大有利于快速迭代，但会增加稳态均方误差和最小均方误差之间的偏差，并可能导致整个迭代过程发散.为了保证较快的预测收敛速度和相对较小的稳态误差，一般给μ设定一个上限:μmax=1/λmax，其中，λmax为输入向量 X(n －1)的自相关矩阵的最大特征值.

3 WPT-FLP算法

WPT-FLP算法具体步骤如下:

①小波包分解与单支重构.选择小波包分解的尺度为N，并对各节点的小波包系数进行单支重构.

②小波包高频系数强制去噪.第N层各节点小波包系数是由第N－1层各节点系数分解得到的，故相对第N－1层系数，第N层小波包系数包含2N－1个低频系数结点即节点(N，0)，(N，2)，…，(N，2N－2)，例如图1(b)第3层小波包分解系数中的 AAA0，ADA2，AAD4与ADD6;第 N 层小波包系数还包含 2N－1个高频系数结点即(N，1)，(N，3)，…，(N，2N－1)，例如图 1(b)中的 DAA1，DDA3，DAD5与DDD7.本步骤对高频系数强制去噪，即将高频系数全部置零.

③小波包低频系数FLP去噪.对步骤②中描述的第N层低频系数进行FLP前向线性预测，在此预测过程中，预测误差与步长是密切相关的.在初始阶段，预测误差较大，步长的选择应该使预测误差快速降到一定的程度，此时可以取相对较大的步长.当预测误差降到一定程度，采用小步长以提高稳态输出精度.由于WPT-FLP权系数调整是基于分频段数据块进行的，因此每个频段步长调整应该和频段内预测误差的绝对误差有关.令第j频段内FLP绝对误差的均值为则可以使用下面的步长增益算法公式［10］:

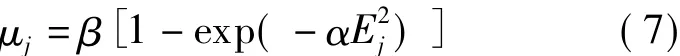
式中，β为由预测过程决定的加权系数;α为衰减系数.可通过多次实验来获得β与α的最优值［11］.为提高算法速度，步骤②和③采用并行处理.

④小波包重构.将步骤②和③分别处理后得到的第N层高低频系数进行重构，得到WPT-FLP算法去噪后的光纤陀螺信号.

4 光纤陀螺信号去噪结果分析

选取一组保偏干涉式闭环光纤陀螺的静态输出信号对算法进行验证，在水平放置、开机稳定、工作环境恒温(30℃)的条件下采集静态陀螺信号，采样频率为100 Hz.取40 s采集的光纤陀螺静态信号对3尺度WPT-FLP算法进行验证，其中小波包的小波基选为db4小波.并与3尺度的小波包去噪、FLP去噪方法进行比较，其结果如图2所示.

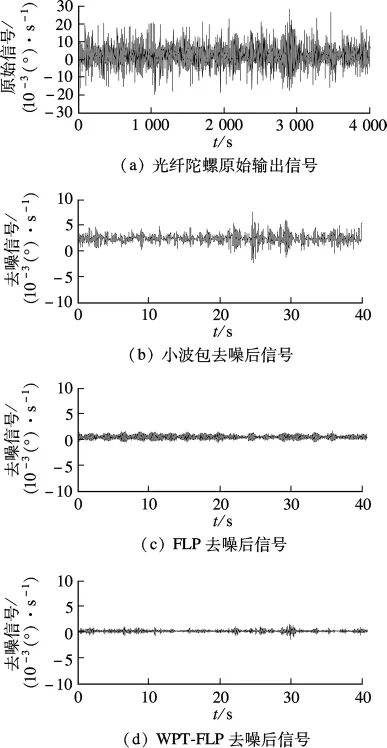
图2 原始信号与去噪结果示意图

由图2(a)可看出，光纤陀螺原始信号噪声较大.由图2(b)、(c)、(d)对比可得，与小波包和FLP算法去噪相比，WPT-FLP算法的去噪效果更好，能更有效地减小噪声对信号的影响.

图3中分别为原始信号和WPT-FLP算法去噪后信号的连续小波变换三维图，对比可得，原始信号的高频系数较大，而WPT-FLP算法处理后的信号则有效地消除了高频系数即噪声的影响.

为定量分析WPT-FLP算法的去噪能力，可通过信号标准差(S)及Allan方差分析［12］中误差系数的变化情况来反映算法的去噪效果.用Allan方差分析中误差系数中的量化噪声(Q)与角度随机游走系数(N)来表征噪声大小，分析结果见表1.

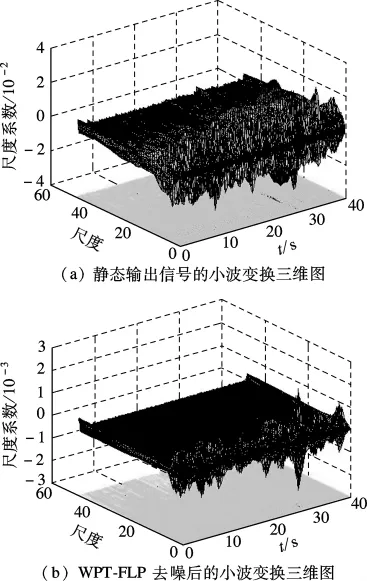
图3 原始信号与去噪后信号的小波变换三维图

表1 去噪前后光纤陀螺信号分析

由表1可看出，相比小波包变换和FLP去噪算法，WPT-FLP算法去噪后的信号其量化噪声、角度随机游走与标准差均有显著下降，表明WPT-FLP算法的去噪能力要优于小波包变换及FLP去噪算法.

5 结语

针对光纤陀螺信号中的噪声，本文结合小波包变换与FLP滤波算法的优势，提出了一种新的去噪方法——WPT-FLP算法.该方法利用小波包变换将输入向量分解到多尺度空间，降低了信号的自相关性，从而提高了FLP算法的去噪精度.利用一组光纤陀螺静态输出信号对去噪算法进行了验证，结果表明，相比于传统的小波包去噪和FLP算法，本文提出的WPT-FLP算法能更有效地降低白噪声对光纤陀螺输出信号的影响，去噪精度更高，且该方法简便易行，易于软件实现.

References)

［1］张桂才.光纤陀螺原理与技术［M］.北京:国防工业出版社，2008.

［2］Blin S，Digonnet M J F，Kino G S.Noise analysis of an air-core fiber optic gyroscope［J］.IEEE Photonics Technology Letters，2007，19(19):1520-1522.

［3］Yan R Q，Gao R X.Harmonic wavelet-based data filtering for enhanced machine defect identification ［J］.Journal of Sound and Vibration，2010，329(15):3203-3217.

［4］ Ji Xunsheng，Wang Shourong，Xu Yishen.Application of fast wavelet transformation in signal processing of MEMS gyroscope［J］.Journal of Southeast University:English Edition，2006，22(4):510-513.

［5］袁瑞铭，孙枫，陈慧.光纤陀螺信号的小波滤波方法研究［J］.哈尔滨工业大学学报，2004，36(9):1235-1238.Yuan Ruiming，Sun Feng，Chen Hui.Wavelet filtering method in signal processing of fiber optic gyro ［J］.Journal of Harbin Institute of Technology，2004，36(9):1235-1238.(in Chinese)

［6］ Wang Qi，Xu Xiaosu.Application of wavelet package filtering in the de-noising of fiber optic gyroscopes［J］.Journal of Southeast University:English Edition，2008，24(1):46-49.

［7］易康，李廷志，吴文启.FLP滤波算法在光纤陀螺信号预处理中的应用［J］.中国惯性技术学报，2005，13(5):58-62.Yi Kang，Li Tingzhi，Wu Wenqi.Application of forward linear prediction filter in signal process of FOG［J］.Journal of Chinese Inertial Technology，2005，13(5):58-62.(in Chinese)

［8］陈世同，孙枫，高伟，等.基于归一化LMS算法的光纤陀螺降噪技术研究［J］.仪器仪表学报，2009，30(3):521-525.Chen Shitong，Sun Feng，Gao Wei，et al.Research on the noise control technology in FOG based on NLMS algorithm ［J］.Chinese Journal of Scientific Instrument，2009，30(3):521-525.(in Chinese)

［9］ He Haibo，Cheng Shijie，Zhang Youbing，et al.Home network power-line communication signal processing based on wavelet packet analysis［J］.IEEE Transactions on Power Delivery，2005，20(3):1879-1885.

［10］吉训生，王寿荣.硅微陀螺信号处理方法——基于前向线性预测小波变换方法［J］.高技术通讯，2008，18(2):151-155.Ji Xunsheng，Wang Shourong.Forward linear prediction based wavelet transformation for micro silicon gyroscope signal processing［J］.Chinese High Technology Letters，2008，18(2):151-155.(in Chinese)

［11］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094-1097.Gao Ying，Xie Shengli.A variable step size LMS adaptive filtering algorithm and its analysis［J］.Acta Electronica Sinca，2001，29(8):1094-1097.(in Chinese)

［12］ Ei-Sheimy Naser，Hou Haiying，Niu Xiaoji.Analysis and modeling of inertial sensors using Allan variance［J］.IEEE Transaction on Instrumentation and Measurement，2008，57(1):140-149.