基于多属性双向拍卖的Web服务选择

赵生慧 吴国新 陈桂林 王汇彬

(1东南大学计算机科学与工程学院，南京 210096)

(2东南大学计算机网络和信息集成教育部重点实验室，南京 210096)

(3滁州学院计算机科学与技术系，滁州 239012)

作为SOA的实现范例，Web服务已经成为Internet应用的标准模式.在Web服务交易市场如何进行互惠的双向选择成为当前Web服务领域的研究热点之一.Web服务的选择研究多侧重于从用户角度，为用户选择一个QoS最优的服务.文献［1］对常用的研究算法包括整数规划法、遗传算法、多目标优化方法等进行了总结，并提出了新的基于多目标粒子群优化的服务选择算法，其目标仍然是选择在一定约束下满足用户的最优服务.拍卖作为一种有效的双向选择方式，在电子交易市场得到了广泛应用.

在早期的拍卖模型中，通常只考虑单物品单属性的拍卖.由于Web服务有功能与非功能2个方面的属性，因此服务消费者对服务的估价和提供者对服务的要价都可以看作基于服务质量的多属性函数，在此基础上的拍卖实质上就是多属性拍卖.Esther等［2］提出了多属性的英式拍卖模型，设计了基于价格和数量的卖方的成本函数和买方的估价函数，为买者设计了期望的最优效用函数;并表示理性的竞买人首先选择独立于当前最高竞拍的最优的非价格属性，然后根据非价格属性给定的值选择一个满足期望的价格.Bichler［3］对各种拍卖形式进行了实验分析，发现在各种拍卖中多属性的拍卖比单属性的拍卖得到的效用大.Che［4］描述了一个多属性拍卖机制，设计了一个考虑多个属性的得分规则，使用得分规则和多属性效用函数，为拍卖方获得更好的收益.文献［5］提出递增叫价的多属性拍卖模型，其中估价函数和成本函数基于每个属性的估计获得.文献［6］对电子采购中的多种拍卖形式进行了总结，并在多属性的拍卖研究中，提出采购拍卖不仅要考虑成本，还要考虑属性.

以上的多属性拍卖研究一般仅考虑一个买方(电子采购)或一个卖方的收益，买方或卖方估价函数使用属性及其权值计算.在实际交易市场中，通常有多个买方和多个卖方，而双向拍卖能够为多个提供者和多个消费者进行交易提供一个良好的协商环境，使得拍卖参与方均能够最大化自己的利益，更加符合市场规则［7］.双向拍卖在网格资源分配和定价方面得到了很好的研究［8-10］.其中，文献［9］将网格中的资源作为网格服务提供给用户，通过引入双向拍卖，描述了一个基于虚拟组织的网格市场体系结构，说明了如何使用双向拍卖对网格服务中的资源进行合理分配.其实网格服务也是Web服务的一类.文献［11］提出基于效用的网格资源分配的双向拍卖方法，根据用户提交的作业和服务提供者提交的资源，在选择过程中使用效用值进行任务分配，既满足提供者的最高效用，也满足用户作业需求.

显然，Web服务作为一种能够被看作按次计费的、在Internet上调用的函数，完全可以使用拍卖进行交易［12-13］.文献［12］利用服务的协商和交互，提出基于拍卖机制的服务定价模型，建立了相应的Web服务领域的拍卖模型，为服务提供者获取最大化收益.文献［13］提出了基于组合拍卖的QoS感知的Web服务组合方法，其中QoS包括提交时间、响应时间、可用性、可靠性等多个服务质量属性.

上述文献中的拍卖模型研究大多基于电子商务，关于Web服务中的拍卖研究较少，所提及的拍卖多是基于单向拍卖，针对Web服务的多属性双向拍卖尚没有发现相关研究文献.本文提出的Web服务领域的基于服务质量属性的双向拍卖机制和基于服务可信度的双向拍卖机制，均考虑了多属性的影响.2个拍卖机制均符合激励相容、预算均衡和个性理性等原则，并满足市场规律.

1 双向拍卖模型

根据机制设计思想，本文设计的拍卖模型如图1所示，包含:m个服务提供者(委托人)及其代理、1个拍卖代理、n个服务消费者 (竞买人)及其代理.在实施拍卖之前，服务提供者和消费者(服务需求者)首先向拍卖代理注册成合法用户，然后才能向拍卖代理提交竞拍.

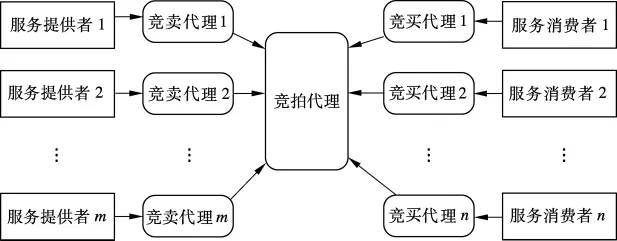
图1 基于双向拍卖的服务选择模型

根据文献［6］的结论，一个合理的拍卖机制应满足激励相容、个体理性和预算均衡.激励相容是指每个代理有一个占优策略.如果代理总是具有占优策略且有非负效用，则说明代理具有个体理性.预算均衡是指当双方的报价改变时，机制设计者不会获得额外的转移支付.

定义1 Web服务拍卖模型是一个五元组A=〈P，C，Po，F，R〉，其中，P 为所有服务提供者集合，P={p1，p2，…，pm};C为所有消费者集合，C={c1，c2，…，cn};Po为服务提供者和服务消费者提交的所有策略集合，Po={B1，B2，S}.B1为服务消费者i提交的第1种竞买策略，表示为SRbi(fi，vi，(q1，q2，…，qK));B2为服务消费者 i提交的第 2 种竞买策略，表示为 SRbi(fi，ri，vi，(w1，w2，…，wK)).其中，fi为服务消费者 i的出价，ri为服务消费者i的可信度，(q1，q2，…，qk)为K个服务质量属性，vi表示竞买Bi对于服务消费者i的价值或价格，(w1，w2，…，wK)为 K个服务质量属性的权值.Sj为服务提供者j提交的竞拍策略，表示为 SPsj(Bidj，cj，(q1，q2，…，qK))，其中 Bidj为服务提供者j的报价，cj为服务提供者j对竞拍Sj的成本.F为P×C×Po→R的映射关系.R为{P，C}匹配结果集，即由拍卖代理根据相应算法进行匹配的结果.

在双向拍卖中，对每个服务而言，服务提供者的成本和服务需求者的价值均是双方的私有信息，也是本文所设计的双向拍卖机制中的类型参数.具有相同功能的服务，不同的服务提供者提供的服务质量可能不同，则成本也可能不同.假设服务双方都是风险中性的，则其效用函数均为拟线性函数.因此，基于多属性的服务提供者的效用函数可表示为:uj(S)=pj(S)－cj(S)，即服务提供者j的一个竞拍S的收益，其中，pj(S)和cj(S)分别为服务提供者j对该竞拍S的叫价和成本(卖者的保留价).同样，不同的服务消费者对服务质量具有不同的偏好，出价也有所不同，则基于多属性的服务消费者的效用函数为:ui(B)=vi(B)－pi(B)，即服务需求者i的一个竞买B的收益，其中vi(B)和pi(B)分别为服务需求者i对该竞买B的价值(买者的保留价)和出价.

机制设计的主要问题就是使所有参与者的效用最大化，且具有激励相容性.从机制设计的角度来看，拍卖就是一组规则，用以决定拍卖的赢家和所有参与者的支付.下面设计的2个双向拍卖机制中，均假设服务提供者之间不存在交易之外的交易，即不存在共谋;任一对服务提供者和服务需求者也不存在共谋，且双方均是理性的参与者;每轮次中参与拍卖的服务双方数量是固定的.在2个拍卖中均遵循Vickery拍卖规则，即拍卖双方用次高价作为成交价.

2 基于服务质量属性的双向拍卖

由于不同服务提供者提供的功能相同的服务可能具有不同的非功能属性，即服务质量属性，本文据此设计了该拍卖算法.在拍卖中，服务双方出价和报价时均携带服务质量属性.

算法1 基于服务质量属性的双向拍卖

输入:竞拍策略 SRs(Bid，c，(q1，q2，…，qK))，即由m个服务提供者向拍卖代理提交的;竞买策略 SRb(f，v，(q1，q2，…，qK))，即由 n 个服务消费者向拍卖代理提交的.

输出:{P，C}的匹配结果集R.

①在一个时间段内，拍卖代理收集服务提供者和需求者提交的竞拍和竞买信息.

②信息收集完毕后，分别对双方报价和出价排序.按服务提供者的报价从低到高排序成一个竞拍列表 SPL(SP(1)，SP(2)，…，SP(m))，排序结果为

对服务消费者的出价从高到低排序成一个竞买列表 SRL((SR(1)，SR(2)，…，SR(n))，排序结果为

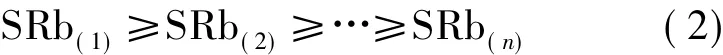
式(1)和(2)中的下标(i)表示参与者在相应列表中的排序位置，每个竞拍和每个竞买都携带其提供的属性集 Q(q1，q2，…，qK).

③拍卖代理按照消费者列表SRL依次取出服务，进行服务质量和价格匹配，直至全部完成.

其中，匹配过程如下:

竞拍或竞买通常是动态变化的.当匹配失败时，由拍卖代理通知相应的消费者退出本轮匹配，或者继续等待进入下一轮，或者降低服务质量需求进入下一轮.

价格p0为双方的出价和叫价的次高价的平均值，p0=(s(j+1)+b(i+1))/2，在此策略的作用下，每个参与者都会理性地选择报价以期与合适的交易者进行交易［14］.

拍卖设计的主要目的是保证服务消费者的服务质量需求得到满足，同时使机制设计者达到最大效用，即服务双方效用最大化.在该算法中，机制是公共知识，而保留价和成本都是双方的私有信息，只有拍卖代理知道他们的保留价(私有值).

定理1 在服务质量属性(q1，q2，…，qK)是公共信息情况下，基于服务质量属性的双向拍卖满足激励相容、预算均衡和个体理性.

激励相容是指所有参与者的真实报告是一个占优策略.这种情况下，任何不诚实的报告所获得的效用都不会比诚实报告优.

预算均衡是指当双方的报价改变时，机制设计者没有获得转移支付.算法1的机制设计者所获得的收益为:si)，因此无论服务提供者和服务需求者如何出价和报价，机制设计者的总收益不变，因此算法1的结果满足预算均衡.

个体理性是指参与拍卖的双方所获得的效用为正或0，即非负效用.算法1中参与拍卖的服务双方所获效用为非负效用，因此其结果满足个体理性.实际上，由于激励相容的特征使服务提供者不能报价太高，消费者出价不能太低，否则获取的效用可能为负或很低.

以上证明可参考文献［8］.

3 基于服务可信度的双向拍卖

在基于服务质量属性的双向拍卖中，服务消费者需要对提供者提供的属性进行成对比较，既增加了匹配时延，也使匹配成功率降低.因此，如果既能兼顾多个属性的影响，又能快速匹配，则会提高成功率.因此，在拍卖中引入服务可信度.

定义2 服务可信度记为ri，指服务消费者对需求的服务是否可信的认可度，表示为属性值及其权值的加权和，即，其中

算法2 基于服务可信度的双向拍卖

输入:m个服务提供者向拍卖代理提交的竞拍信息 SRs(Bid，c，(q1，q2，…，qK))，n 个服务消费者向拍卖代理提交的竞买信息 SRb(f，r，v，(w1，w2，…，wK)).

输出:{P，C}的匹配结果集R.

①在一个时间段内，拍卖代理收集服务提供者和需求者提交的竞拍和竞买信息.

②与第2节中基于服务质量属性的双向拍卖中的步骤②相同.

③拍卖代理按照消费者列表SRL依次取出服务，进行服务质量匹配，直至全部完成.

其中，匹配过程如下:

当匹配失败时，由拍卖代理通知相应的消费者退出本轮匹配，或者继续等待进入下一轮，或者降低服务可信度需求进入下一轮.

定理2 在服务可信度ri为公共信息情况下，基于服务可信度的双向拍卖满足激励相容、预算均衡和个体理性.

定理2的分析同定理1.

4 拍卖模型仿真分析

4.1 实验环境

实验仿真程序使用Java语言编写.实验中，服务提供者的叫价和服务消费者的出价均服从均匀分布，分别为［10，20］及［12，22］.其中出价和叫价的边界有包含关系，以防止过高的叫价导致交易率过低的现象.为了便于实验，服务质量属性只有2个，属性值均服从均匀分布［0.6，1).对应的权值为(t1，t2)，t1服从正态分布(0.6，0.1)，t2=1 － t1.服务提供者的成本是当前叫价的70%，消费者的价值(即保留价)高于出价30%.

为了验证2个拍卖机制的效率，实验中使用2个参数来衡量:平均交易成功率和平均机制总收益.交易成功率是指每轮交易的成功匹配占总匹配的比例(总匹配数为m和n中的最小数).机制总收益是指机制所获得的每个成功匹配的盈余，即.取运行相应轮次的平均值，得到平均交易成功率和平均机制总收益.

4.2 实验分析

为了比较服务交易中不同数量参与者的匹配成功率和机制的总收益，先进行服务提供者和服务消费者个数相等(m=n)时，分别取值20，30，40，50，60，80的实验.各个实验的运行轮次均为800次.图2(a)和(b)分别给出了基于服务质量属性和基于服务可信度的双向拍卖结果.从图2可看出，当服务提供者和消费者参与的个数逐步增多，交易成功率也逐步上升，而总收益几乎呈线性增长，这完全符合市场规律.显然，在相同参与者数量下，图2(b)中平均交易成功率和总收益相对于图2(a)中较高.

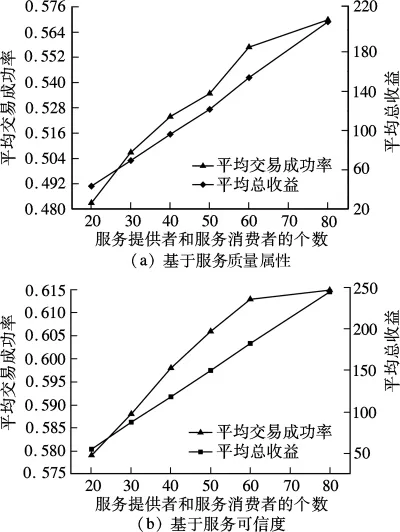
图2 基于服务质量属性和服务可信度的双向拍卖结果

图3为服务提供者和消费者均为40的情况下，分别运行 100，200，400，600，800，1 200，2 000次的结果.图中，平均交易成功率在0.520～0.527之间，平均总收益在95.4～97.7之间，说明运行轮次对交易成功率和平均总收益的影响不明显，表明了算法的稳定性.在执行基于服务可信度的相同实验时，平均成功率集中在0.592～0.597之间，平均总收益在117.2～118.5之间.

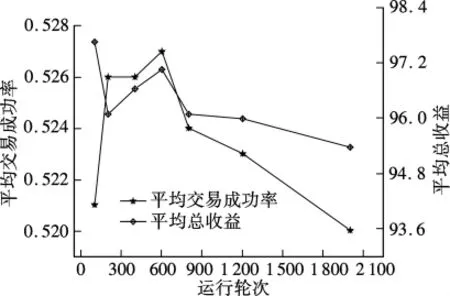
图3 不同运行次数的平均交易成功率和平均总收益比较

上述实验结果说明，考虑多个质量属性的双向拍卖中每个属性均要满足需求，因此一轮竞拍中成功的匹配比率相对较小，效率较低.而基于服务可信度的双向拍卖由于将多个属性综合考虑，不局限于单个属性需求，因此相同条件下成功匹配率高于基于服务质量可信度的双向拍卖.

5 结语

在Web服务市场中，由于交易机制的不完善，不能充分体现服务提供者与服务消费者双方的利益诉求，也不能实现服务双方的收益均衡，影响了双方的交易积极性和交易成功率.本文提出了基于服务质量的双向拍卖，在此基础上，定义了由服务质量属性及其权值线性加权的服务可信度概念，并提出了基于服务可信度的双向拍卖.仿真实验结果表明，在多属性双向拍卖机制中，服务双方能够在要价与还价的过程中充分表达自己的市场及收益预期，交易结果能够达到服务双方的收益均衡，实现总体收益最大化，客观上也能够促进服务交易的开展并提高交易的成功率.未来将针对参与者随机变化及多服务拍卖的实际情况开展相关模型及算法的研究.

References)

［1］孙学胜，曹玖新，刘波，等.基于多目标粒子群优化的服务选择算法［J］.东南大学学报:自然科学版，2009，39(4):684-689.Sun Xuesheng，Cao Jiuxin，Liu Bo，et al.Service selection algorithm based on multi-objective particle swarm optimization［J］.Journal of Southeast University:Natural Science Edition，2009，39(4):684-689.(in Chinese)

［2］ Esther D，Rina A，Sarit K.An English auction protocol for multi-attribute items［C］//AMEC-IV LNCS 2531.Springer，2002:52-68.

［3］ Bichler M.An experimental analysis of multi-attribute auctions［J］.Decision Support System，2000，29(3):249-268.

［4］ Che Y-K.Design competition through multidimensional auctions［J］.Rand Journal of Economics，1993，24(4):668-680.

［5］金涬，石纯一.一种递增叫价的多属性拍卖方法［J］.计算机研究与发展，2006，43(7):1135-1141.Jin Xing，Shi Chunyi.An ascending bid multi-attribute auction method［J］.Journal of Computer Research and Development，2006，43(7):1135-1141.(in Chinese)

［6］ Chandrashekar T S，Narahari Y，Rosa C H，et al.Auction based mechanisms for electronic procurement［J］.IEEE Transactions on Automation Science and Engineering，2007，4(3):297-321.

［7］ McAfree R P.A dominant strategy double auction［J］.Journal of Economic Theory，1992，56(2):434-450.

［8］翁楚良，陆鑫达.一种基于双向拍卖机制的计算网格资源分配方法［J］.计算机学报，2006，29(6):1004-1009.Weng Chuliang，Lu Xinda.A double auction method for resource allocation on computational grids［J］.Chinese Journal of Computer，2006，29(6):1004-1009.(in Chinese)

［9］ Joita L，Rana O F，Gray W A，et al.A double auction economic model for grid services［C］//Euro-Par 2004 Parallel Processing LNCS 3149.Pisa，Italy，2004:409-416.

［10］李立，刘元安，马晓雷.基于组合双向拍卖的网格资源分配［J］.电子学报，2009，37(1):165-169.Li Li，Liu Yuanan，Ma Xiaolei.Grid resource allocation based on the combinatorial double auction［J］.Acta Electronica Sinica，2009，37(1):165-169.(in Chinese)

［11］ Chainan S，Ryusuke E，Hiroyuki T，et al.A utilitybased double auction mechanism for efficient grid resource allocation［C］//IEEE International Symposium on Parallel and Distributed Processing with Applications.Chengdu，China，2008:252-260.

［12］ Zhang Jia，Zhang Ning，Zhang Liangjie.Auctionbased pricing model for Web service providers［J］.International Journal of Web Services Research，2006，3(3):82-107.

［13］Mohabey M，Narahari Y，Mallick S，et al.A combinatorial procurement auction for QoS-aware Web services composition［C］//IEEE International Conference on Automation Science and Engineering.Scottsdale，AZ，USA，2007:716-721.

［14］ Despotovic Z，Usunier J，Aberer K.Towards peer-topeer double auctioning［C］//37th Hawaii International Conference on System Science.Big Island，Hawaii，USA，2004:1-8.