MEMS磁场传感器的设计及测试

陈 洁 秦 明 黄庆安

(东南大学MEMS教育部重点实验室，南京 210096)

磁场传感器广泛用于汽车、轮船和飞机的高精确度导航和定位，能够实现医学生物电检测和疾病检测等，可以获取异常微弱的信号和探索危险以及人类不能够到达的领域.

随着微电子机械系统(micro-electro-mechanical systems，MEMS)的发展，磁场传感器向小型化和微型化发展，不仅降低了制作成本，还可以完成许多大尺寸机电系统所不能完成的任务.和传统器件相比，MEMS磁场传感器具有体积小、重量轻、功耗低、成本低、可靠性高、性能优异及功能强大等传统传感器无法比拟的优点.

20世纪后期，磁通门器件和霍尔器件广泛地应用于磁场测量，这些器件尺寸小，可以和CMOS工艺兼容，性价比较高，但是此类器件功耗高，限制了其发展［1］.近年来，随着 MEMS技术的发展，研制出了多种微型化的磁场传感器，如法国的Latorre等［2-4］提出的悬臂梁结构的MEMS磁场传感器，此结构在悬臂梁的根部集成压阻，通过测量压阻的输出得到结构在磁场作用下受洛伦兹力后产生的变形.扭摆式MEMS磁场传感器最早由Eyre等［5］提出，该传感器通过测量在磁场作用下受力后结构扭摆的幅度得到磁场的大小.Sunier等［6］提出的谐振式磁场传感器，受力以后结构谐振频率发生变化，由此实现磁场测量.Brugger等［7-9］提出了一种谐振式磁场传感器，此种传感器包括一个两端有间隙的磁聚能器，制作时需使用软磁材料.上述这些磁场传感器主要用于测量磁场的大小，不能分辨磁场的方向.Allen等［10-12］提出了一种梳齿磁场传感器，利用永磁体和磁场的相互作用使梳齿发生偏转，用来测量磁场的方向，但这种结构中含有永磁体，不能采用标准的CMOS工艺加工，无法与处理电路相集成.

本文提出了一种新的磁场检测方法，用于磁场检测的传感器采用标准CMOS工艺和后处理来实现.该传感器采用电磁感应的测量原理，结构简单，便于测量，功耗低，受温度影响小.

1 传感器工作原理

本文提出的磁场传感器结构主要是由U型梁构成，结构如图1所示，梁上镀金属线，可以看作是一层金属导线，导线从梁的一侧进入，环绕梁一周以后从梁的另外一侧流出，形成回路.当金属线上通电流时，在磁场作用下金属线上受力结构就会摆动或者振动.

图1 谐振结构磁场传感器

当金属线通上正弦电流后，由于磁场方向与结构上的金属线(长度为l1)垂直(见图1)，与支撑梁平行，所以支撑梁上金属线不产生洛伦兹力，只有结构顶部金属线(长度为l1)上产生洛伦兹力，即

式中，i为正弦电流;B为磁场强度.

将此结构等效看作弹簧质量块系统，则

式中，k为结构的刚性系数;x为结构振动的幅度.

由于结构被看作弹簧质量块系统，因此结构的振动幅度可表示为

式中，A为结构的振幅;ω为振动的角速度;φ为结构振动的初相角.

由此得到金属线的振动速度为

由式(1)～(4)联立得到

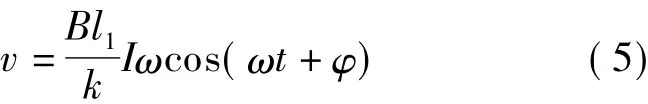
当结构振动时，金属线会随着结构一起振动，在磁场作用下金属线上就会产生感生电动势ξ，

为了提高传感器的灵敏度，使结构在谐振频率处振动，得到感生电动势为

式中，Q为结构在振动时的品质因子.结构在正弦电流的作用下会产生振动，当所加的电流频率和结构本振频率相同时，结构就会谐振，此时振幅达到最大.

2 传感器模拟和仿真

为了优化传感器的性能，利用ANSYS有限元分析工具对其进行模拟与仿真.传感器是采用结构振动时金属线切割磁场产生感生电动势来达到测量磁场的目的.为了能够测量出感生电动势，U型梁的前端应该是对称形式的振动.如果是反对称形式的振动，感生电动势就会相互抵消，不利于测量.对传感器的谐振频率和振动模态进行了模拟，模拟过程中结构的一些机械参数如表1所示.

表1 有限元模拟使用的参数

由振动理论可知，振动时模态较低产生的响应较大，所以本文对结构的前4阶模态进行了模拟，得到的结构前4阶振动模态如图2所示.

图2 U型结构前4阶模态

从图2中可看出，不同的模态下结构的振动模式不同，一阶和二阶模态运动主要以整体平行摆动和转动为主，三阶模态是在一阶摆动的基础上加上了扭动的弯曲振动;一阶和三阶的运动是对称形式的运动，二阶和四阶的运动是反对称形式的运动.从模态分析可看出，一阶和三阶模态较利于测量.通过模拟仿真得到的频率分别为1.99，5.87，16.92，23.93 kHz.

图3为U型梁频率响应的测试曲线.可看出，一阶和三阶频率分别为2.12和16.02 kHz，偶次谐波被压制，所得到的运动频率和模拟的基本接近，两者的误差为6.26%和5.30%.

图3 U型梁频率响应曲线

3 传感器加工

传感器采用PN结自停止腐蚀工艺释放完成.首先对4英寸(10.16 cm)的硅片进行N+扩散和氧化，扩散层的厚度和梁最终的厚度相同，接着溅射金属并刻蚀引线，然后背面电化学腐蚀衬底到N+扩散层停止，最后正面ICP释放结构，具体工艺过程如图4所示.所得到的结构如图5所示.

4 测试结果及分析

图4 传感器的制造工艺流程图

图5 传感器结构图

当在结构的金属线上加电流时，在磁场作用下结构就会受力的作用，并且随着磁场的改变，结构上受力的大小和方向也会随之发生改变，这样就会影响结构的振动和摆动的幅度.所加的磁场平行于平板所在平面，并与支撑梁方向平行.

对结构在磁场作用下的振动幅度进行了测试，由于测量所得到的信号较小，所以在测试时需要接放大电路.由于放大电路在低频时噪声干扰较大，所以本实验利用三阶模态进行测量，所对应的频率为16.02 kHz.采用多普勒仪直接测量结构在振动时的振幅，图6为U型梁金属线加上电流多次测量所得到的振幅曲线，结构上所加的电流(I)从2 mA到20 mA不断增加，电流的频率为16.02 kHz(对应三阶模态的频率)，所加的磁场强度(B)为88 mT.从图6中可看出，随着金属线上所加电流的增加，结构的振动幅度也随之增大，电流在2～20 mA变化范围内，振幅变化约为250 nm，基本成线性变化，与理论预测的结果符合.

图6 传感器电流与振幅关系图

图7给出了磁场与振动幅度的关系曲线，测量时振动幅度采用多次测量得到.由图7可看出，激励电流固定不变(10 mA)时，磁场的变化影响了振动的幅度，随磁场的增加结构的振动幅度也增加，基本成线性关系.

图7 磁场强度与振幅关系

本文中的传感器只包含一根金属线，被先后用于U型梁的激励和检测.金属线首先加上正弦电流，此时由于在磁场中受到洛伦兹力的作用，梁产生振动;然后将此电流断开，由于梁在谐振频率点振动，结构仍然处于振动状态，此时在磁场中产生的感生电动势即为传感器的输出信号.由于所测量的感生电动势较小，所以在测试时增加了测量放大电路，放大倍数约为3×104倍.图8给出了结构在磁场作用下的输出电压波形与磁场的关系.从图8可看出，在电流分别为6和10 mA情况下，输出的感生电动势随磁场的增大而增加，基本成二次曲线的关系，与理论趋势相吻合;随着电流的增加灵敏度也提高了，输出信号放大后实验所得到的最大灵敏度在磁场为29 mT的位置，其值为14 mV/mT.图9给出了输出电压与输入电流的变化曲线，当磁场强度固定为88 mT时，电流从2 mA逐渐增加到16 mA，可看出随着电流不断增加，感生电动势的输出也随着相应变大，基本成线性关系，与放大相应倍数的模拟结果对比，最大误差小于5%.

图8 输出电压与磁场强度的关系

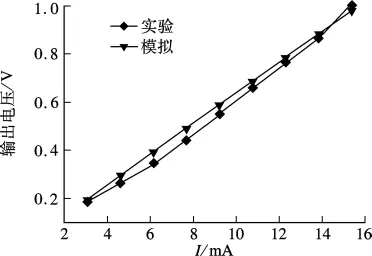
图9 输出电压与激励电流关系

5 结语

本文利用微电子机械加工技术研制出一种结构简单的新型磁场传感器.并采用ANSYS软件对传感器的频率及不同的模态振动方式进行了模拟，有限元模拟结果表明该结构可以用于磁场的测量.实验测试表明该传感器在磁场强度为mT范围有明显的响应，输出结果和理论及模拟结果基本吻合.所得到的输出结果是经过放大滤波电路得到的，测试得到的灵敏度为14 mV/mT.

References)

［1］ Lenz J E.A review of magnetic sensors［C］//Proceedings of theIEEE. Piscataway， NJ， USA， 1990:973-989.

［2］ Baglio S，Latorre L，Nouet P.Resonant magnetic field microsensors in standard CMOS technology［C］//Instrumentation and Measurement Technology Conference.Venice，Italy，1999:452-457.

［3］ Beroulle V，Bertrand Y，Latorre L，et al.Monolithic piezoresistive CMOS magnetic field sensors［J］.Sensors and Actuators A:Physical，2003，103(1):23-32.

［4］ Dumas N，Azais F，Latorre L，et al.On-chip electrothermal stimulus generation for a MEMS-based magnetic field sensor［C］//Proceedings of the 23rd IEEE VLSI Test Symposium.Palm Springs，CA，USA，2005:213-218.

［5］Eyre B，Pister K S J，Kaiser W.Resonant mechanical magnetic sensor in standard CMOS［J］.IEEE Electron Device Letters，1998，19(12):496-498.

［6］Sunier R，Vancura T，Li Y，et al.Resonant magnetic field sensor with frequency output［J］.Journal of Microelectromechanical Systems， 2006， 15 (5):1098-1107.

［7］Brugger S，Simon P，Paul O.Field concentrator based resonant magnetic sensor［C］//IEEE Conference on SENSORS.Daegu，Korea，2006:1016-1019.

［8］ Brugger S，Paul O.Resonant magnetic microsensor with μT resolution［C］//IEEE Conference on MEMS.Tucson，AZ，USA，2008:944-947.

［9］ Brugger S，Paul O.Field-concentrator-based resonant magnetic sensor with integrated planar coils［J］.Journal of Micromechanics and Microengineering，2009，18(6):1432-1443.

［10］ Leichle T C，Ye W，Allen M G.A sub-μW micromachined magnetic compass［C］//IEEE Conference on SENSORS.Kyoto，Japan，2003:514-517.

［11］ Leichle T C，Arx1 M V，Reiman S，et al.A lowpower resonant micromachined compass［J］.Journal of Micromechanics and Microengineering，2004，14(4):462-470.

［12］Choi S，Kim S H，Yoon Y K，et al.A magnetically excited and sensed MEMS-based resonant compass［J］.IEEE Transactions on Magnetics，2006，42(10):3506-3508.