基于失配控制的非线性补偿带隙基准电路设计
2011-08-24聂卫东常昌远
吴 金 聂卫东 常昌远 渠 宁, 李 浩,
(1东南大学无锡分校,无锡 214135)
(2江南大学物联网工程学院,无锡 214122)
(3东南大学集成电路学院,南京 210096)
电压和电流基准作为高精度静态功能电路,在数模混合集成电路中有极广泛的应用,其性能在很大程度上决定了系统信号处理与控制的精度水平.然而,现有的一阶线性补偿带隙基准,因其固有的非线性温度量,其较高的温度系数已无法满足部分超高精度系统应用的需求.在此基础上发展起来的各类高阶非线性补偿技术,虽然理论上可将基准温度系数控制在 1 ×10-6/℃以内[1-2],但因工艺漂移与匹配误差的影响以及低压低功耗的限制,实际温度系数大于10×10-6/℃且呈现较大的离散性[3-4].增加输出修调控制后,电压基准实际温度系数虽略有下降[5-6],但与仿真结果相比仍有较大差距.
基准输出的电源电压稳定性依赖于电路所采用的自偏置结构,温度稳定性则依赖于高阶非线性温度补偿结构.高阶补偿结构中相关器件参数随工艺条件的变化,是导致基准温度特性严重退化、基准输出一致性与均匀性变差的主要原因,增大了输出基准修调的难度.因此,高阶温度补偿不但应有最佳的补偿效果,同时还要求具有最简单的补偿结构,以抑制工艺漂移和工艺误差对高精度基准温度特性的影响.
在常规高阶非线性补偿原理和结构分析的基础上,基于系统失配控制的高阶基准补偿方法,并采用CSMC 0.18 μm CMOS工艺完成了基准电路的设计,给出了电路温度特性的仿真分析结果.实际流片测试结果验证了补偿方法的有效性,结合电路结构误差分析,总结了高精度基准电路设计的基本原则和方法.
1 基于失配控制的非线性补偿方法
基准高阶补偿的目的是消除基准中残留的非线性量,因此首先简要分析一阶线性补偿基准中残存的非线性温度特性,并根据非线性补偿的基本原则,提出基于电路系统失配非线性补偿控制的新方法与结构.
1.1 非线性温度特性
半导体材料及器件参数多为温度敏感的,因此电压或电流基准通常只能采用基于正负固定温度系数物理量补偿叠加的方式实现.PN结导通电压VBE具有近似-2.0~-1.8 mV/℃的固定负温度系数;电流相同但面积不同的2个PN结,其导通电压之差ΔVBE∝VT=kT/q,其中k为玻尔兹曼常数,q为电子电荷量,T为绝对温度.热电压VT正比于绝对温度,其理想条件下的固定正温度系数为+0.087 mV/℃.将以上2种温度系数相反的电压进行叠加,得到的一阶线性基准为Vref_I=VBE+mVT,其中线性补偿系数m由正负温度系数的比值确定,m≈20~23,因此电压模基准输出固定在1.2 V附近.
显然,VBE中存在的温度非线性量无法由线性温度电压mVT进行补偿,因此在Vref_I中必然残留有非线性温度量.忽略电路误差,理想补偿条件下的一阶线性补偿基准输出为
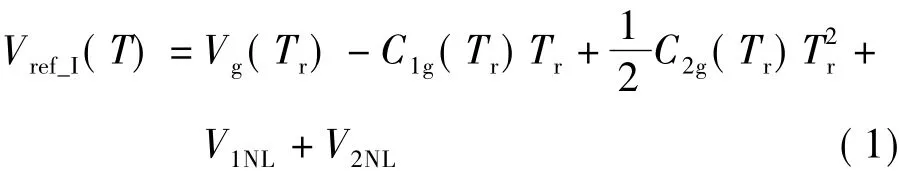
式中,Tr为参考温度;C1g和C2g分别为硅能隙电压Vg(T)的一阶与二阶温度系数.式(1)中的前2项构成了理想基准输出Vref_0,输出的非线性电压量V1NL与V2NL则分别来源于VBE与Vg中非线性电压的贡献[7],并有
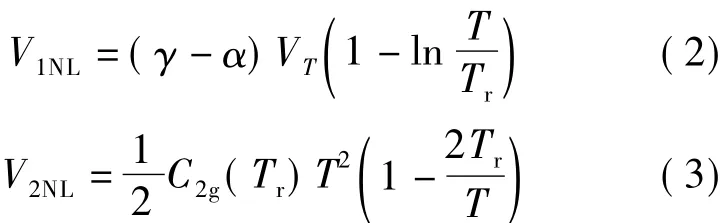
式中,参变量 γ=4-n,α=1-C1R1Tr,其中 -n为载流子迁移率指数负温度系数,C1R1为电阻一阶线性温度系数.随掺杂浓度变化,n的取值范围为0.8~2,采用负温度系数多晶电阻可通过增加α而使γ-α减小,抑制基准中的非线性.SMIC 0.13 μm和CSMC 0.5 μm工艺下的γ-α分别为1.30和1.64,即通常有γ-α>0.若特定工艺存在漂移,同样可引起γ-α值即基准中非线性电压的变化.
由于C2g<0,当γ-α>0时温度特性曲线开口向下,在Tr下基准输出最大且温度系数为零.理论上,只有在γ-α<0的条件下,才有可能出现开口向上的温度特性曲线.无论开口方向如何,一阶线性补偿只能在Tr下得到单峰值输出,调节系数m可获得对称平衡的温度曲线,最大程度地降低温度系数;在对称平衡条件下,完整温度范围内基准变化约为1.6~2.0 mV,对应的温度系数为(5~10)×10-6/℃.适当微调m值,基准温度特性曲线将由对称变为非对称型,温度系数显著退化.
1.2 基于失配控制的分段补偿方法
根据式(1)模型,为获得理想基准Vref_0输出,附加的非线性补偿电压VCNL应能完全抵消一阶线性补偿基准中残留的全部非线性电压,即满足VCNL=-(V1NL+V2NL)的约束条件.对于基准中残留的非线性温度复杂的变化特性,难以在整个温度范围内找到一个简单补偿结构以生成所需的补偿电压.为此,分段补偿控制显示出独有的优越性[8-10].为配合分段补偿,首先将一阶线性补偿的理想m值略微降低,使获得的开口向下温度特性曲线呈现一定的非对称性,即高温段的负温度系数略有增加.此时,对附加补偿结构的要求仅为在高温下提供正温度系数补偿电压,将此补偿量加到非对称一阶线性基准中,即可获得对称平衡的“M”形二阶补偿温度曲线.显然,分段补偿策略的最大优点在于因温度范围的压缩,非线性补偿电压形成的难度降低、补偿结构简化.由于分段补偿依赖于一阶线性补偿与高阶补偿的紧密配合,调节难度大,更关键的是,当工艺发生漂移时,补偿管参数随之漂移,线性与非线性补偿失配,使传统分段补偿基准的工艺稳定性难以有效改善.
为避免采用附加补偿元件因工艺漂移带来的补偿误差,提高基准的工艺稳定性,可通过器件参数与电路工作状态点的设置,即利用极性与大小可配置的系统失调完成高阶非线性补偿.为使该补偿方法有效,必须最大程度地抑制电路中的随机失调和误差,而大幅降低电路存在的随机误差,只能以牺牲电路面积为代价,增大元器件尺寸,设计严格对称匹配的版图,使电路工作点失配形成的系统失调占据主导地位.为避免运放随机输入失调的影响,采用基于电流镜控制的基准电路结构,其典型结构如图1所示.

图1 2路自偏置基准结构
当自偏置结构中MN0和MN1两管所在支路电流I0与I1因工作点失配,产生ΔI的绝对偏差,其相对偏差 εS=ΔI/I0,则有 I1/I0=1+εS.此时,在εS≪1的条件下,偏置电路通过电阻R0产生的实际支路电流为

式中,N为图1中Q0和Q1两衬底PNP管发射区面积之比.忽略线性电流镜传输电流的误差以及输出电流变化对PN结导通电压的影响,偏置电流的变化量传递到输出后,在输出支路电阻R2上形成的偏差构成了高阶补偿电压,即
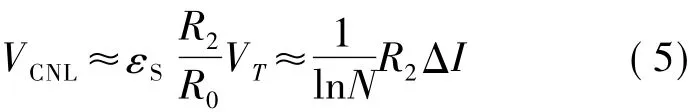
在SPICE模型中对输出支路电阻R2采用二阶非线性温度模型,即

式中,C1R2,C2R2为电阻 R2的一阶和二阶温度系数,且 C1R2<0,C2R2>0,二者分别在中低温与中高温范围内起作用.通常,利用输出电阻及失配电流I的非线性温度特性,获得不同温度范围下正、负温度系数的补偿量.在I为与温度无关的固定常数的简化条件下,只需通过I正负极性控制和大小设置,同时结合电阻的非线性温度特性,即可获得在中低、中高温度范围内有效的不同性质的温度补偿量.
实际条件下I与温度有关,I的温度特性虽然丰富了温度调节的手段,但参数最优点调节的难度增加.设相对参考温度Tr的温度范围为ΔT=TTr,失配电流的一阶温度系数为 C1ΔI= ∂ΔI/∂T,受ΔI与C1ΔI调制的一阶与二阶有效温度范围分别为

由失配电流经电阻转换得到的误差电压具有非线性温度补偿特性,即
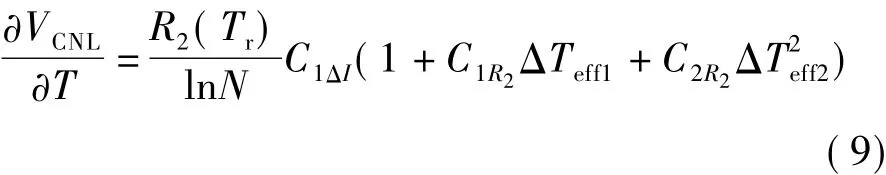
因此,VCNL可以提供电路在不同温度范围内高阶非线性补偿所需的正、负温度系数电压量.
2 基于失配补偿的基准电路设计
2路自偏置结构虽然存在电流失配,但无法通过内部结点电位的调节自由设置其极性和强弱,因此无法用于可控的非线性补偿.将2路自偏置扩展为3路自偏置结构后,以上问题得以解决,由此得到的基于系统失配误差控制的非线性补偿带隙基准电路如图2所示,同时将普通的PMOS电流镜改为宽摆幅共源共栅电流镜以提高偏置电流的传递精度.为提高匹配精度,除PMA和PMB两管构成的启动电路外,基准中的各支路电流全部设定为相同.这样,通过调节PM7相对于PM3管的宽长比的大小,就可调节这2管栅压的相对大小,从而造成MN0和MN1两管漏电压的失配,进而引入2支路的失配电流ΔI,失配电流的极性和大小可以通过漏电压的失配精确控制.

图2 3路自偏置失调控制基准电路
根据失调电压可灵活配置的特点,电路参数的设计应与总体补偿策略相适应.当电路设定在匹配模式下,即对应结点电压匹配使ΔI≈0时,则在特定的线性补偿系数m0下可获得近似平衡对称且开口向下的温度特性曲线,并作为高阶补偿调节的初始条件.由于m=(R2/R0)lnN,其中N值通常为固定值,R0电阻因决定了偏置支路电流的大小并涉及系统静态功耗,一般也为固定值,因此主要依靠调节输出电阻R2控制补偿系数m的大小.当初始状态确定完成后,继续微调m值将破坏基准输出温度特性的对称性,此时通过MOS管尺寸参数失配最终引入电流失配,若电流失配与m值两者协同微调时,一定存在使基准温度系数最小的状态.选取高温分段补偿策略可确保获得以上最佳状态,即调节m使其略小于平衡模式下的m0,则高温段负温度系数略强,通过调节PM7管的宽长比控制失配量,即增强中高温下的正温度系数,最终可获得近似对称的“M”形基准温度特性曲线.
失配控制方法补偿得到了基于CSMC 0.18 μm CMOS工艺SPICE电路仿真结果的验证.图3(a)为一阶线性补偿开口向下的对称式温度特性曲线,在-40~125℃的温度范围内,温度系数约为4.6×10-6/℃;图3(b)为二阶高温分段补偿得到的对称式“M”形温度特性曲线,在相同的温度范围内温度系数降低到1.2×10-6/℃.
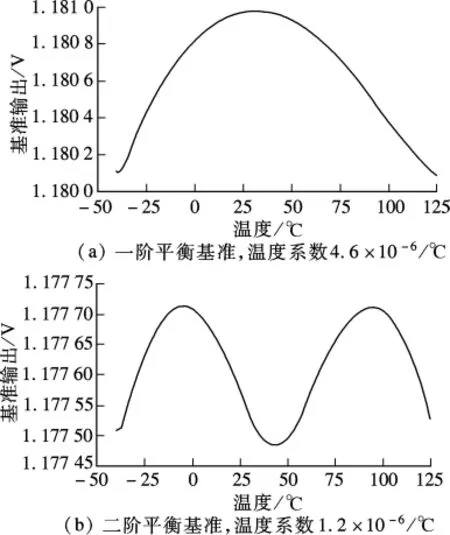
图3 系统失配补偿的带隙基准温度特性
进一步的工艺角变化仿真结果表明,一阶线性补偿由于相对较好的状态对称匹配性,在MOS管、BJT管、电阻的各个工艺角变化下温度系数变化很小,而高阶补偿由于存在失调与偏差,导致温度系数随工艺角的变化而产生明显的退化.工艺对基准的影响不仅体现在上述工艺角的变化中,即使工艺角不变,受工艺匹配精度的限制,因器件图形尺寸参数、开启电压偏差引入的MOS管失配、BJT管失配和电阻失配等,同样可使基准电路的精度特性退化.各类失配的随机性决定了无法依靠相互间的抵消作用以消除误差,只能降低各类失调误差的绝对数值.其中,除增加元器件尺寸面积降低失调的共性要求外,还需增加MOS管过驱动电压以减小阈值电压失配带来的电流镜传输误差;减小基极串联电阻偏差以减小Q管失配.基于以上原则,对于采用的CSMC 0.18 μm CMOS工艺,各元器件均选取较大尺寸设计,其中MOS管最小沟长均为2 μm,决定偏置支路电流的R0电阻线条宽度取6 μm,所有Q管的最小发射区面积为10 μm×10 μm.此外,所有元器件均采用严格对称的版图匹配设计,利用冗余结构保证版图单元的均匀性,以使电路中特定设计的系统失调超出工艺随机失调的作用,实现接近理想状态下的基准补偿特性.
然而,工艺参数的漂移和元器件的随机失配在实际工艺条件下总是无法避免的,因此理论上固定模式的补偿结构无法满足不同芯片的个性化误差补偿需求,高精度基准特性的实现很大程度上依赖输出修调控制.其中,对偏置电阻R0的人为修调可调节静态工作点电流,克服工艺漂移的影响,使电路处于具有最小温度系数点的工作状态和模式,较宽的电阻调节范围有助于抑制工艺漂移变化的影响;其次,对偏置电阻R0或输出电阻R2的修调可控制电阻相对误差的极性与数值,使其与电流镜产生的误差完全抵消.实现电路设计所具有的超低温度系数需要尽可能地提高电阻修调的精度.为简化修调结构,本文仅对输出电阻R2进行修调控制,利用输出修调Pad的选择性短路方式双向调整电阻阻值,其修调覆盖相对范围达到±17%,以满足工艺宽范围变化的需求.
3 测试结果分析
对本文基于CSMC 0.18 μm CMOS工艺设计的基准电路进行了流片验证,图4为芯片的显微照片,芯片面积为230 μm ×230 μm.图5给出了同一基准电路在不同电压下温度特性的测试结果,其中在3 V电源电压下以及-20~120℃的温度范围内,经修调后基准最小温度系数为6.2×10-6/℃,当电源电压下降或温度范围继续向低温范围扩展后,温度系数都将有明显的退化,说明电路内部工作状态点的微小变化确实对基准输出特性产生了影响.

图4 芯片显微照片

图5 基准温度特性曲线测试结果
最佳测试结果虽然离预期基准理想温度特性仍有一定距离,但理论预测的温度曲线变化规律在实测结果中得到了初步验证.受测试仪器内阻的影响,基准输出的中心值略有降低.电路中各类与工艺相关的随机误差累加造成的电路失配,是基准温度系数实测结果无法达到理想状态的根源.
电路中各电流镜均为1∶1的线性传输比,对电阻比、面积比等比值大于1的传输因子则采用基本单元的并联结构.对于匹配结构产生的失配,电流镜相对误差为δCM,电阻与Q管的相对误差分别为δR和 δQ.工艺漂移产生的电阻误差为 εR,线性补偿系数偏差为Δm.最差条件下各类偏差失调极性相同形成误差的累加输出,则最大偏差相对热电压的归一化值近似为

降低输出偏差只有抑制各元器件的相对误差,由于采用基于单元构建的对称匹配设计,则各元件的相对误差最终由各自元件基本单元的相对误差决定.除与工艺有关外,基本元器件单元的相对误差还与其图形尺寸面积、工作电压条件等紧密相关.根据本文基准电路采用的参数与工作条件,参考CSMC 1.0 μm 和0.5 μm CMOS工艺的相关实测数据估算,工艺漂移下的偏差为Δm≈0.2,电阻偏差为 εR=20%;失配误差 δCM≈2.0%,δR≈0.4%,δQ=0.06%.在本文电路的工作条件下,m≈20,Q管面积比N=8,电流镜误差是输出总误差的最主要来源,电阻次之,Q管最小并可忽略.以上各类误差叠加后累积的最大总误差接近甚至达到热电压VT,即输出20 mV的偏差相当于引入50×10-6/℃的温度系数变化,与芯片输出电压及温度系数偏差的实际测试变化范围相吻合.
若设计的电阻修调范围略大,在有限修调Pad数量的约束下,电阻的修调精度偏低,而且仅对输出电阻修调无法调节电路的最佳状态点,造成基准电路实际的温度性能偏离理想设计目标.因此,电阻修调范围与精度控制需折中选择.
4 结语
高阶非线性补偿是实现高精度基准的基本方法,由于超低温度系数的实现受工艺漂移和单元匹配误差的限制,因此对电路中各类误差的有效控制成为高精度基准电路设计的关键[10-11].本文采用的基于系统失配控制的高阶补偿方法建立在系统失调极性与大小精确可控的基础上,相比常规分段补偿方法,消除了补偿元件产生的失调,同时采用输出电阻修调结构进一步抑制了工艺漂移与工艺随机失配对高阶补偿基准精度的影响.实验结果表明,提出的基于失配控制的高温分段补偿方法,适用于对一阶线性基准中非线性温度量的补偿,在电路精度可控的条件下,采用失调控制可有效降低输出基准的温度系数.
References)
[1] Koudounas S,Andreou C M,Georgiou J.A novel CMOS bandgap reference circuit with improved high-order temperature compensation[C]//Proceedings of IEEE International Symposium on Circuits and Systems.Pairs,2010:4073-4076.
[2] Li Yan,Wu Jin,Huang Zhiqi,et al.A sub-1 ppm/℃high-ordercurvature-compensated bandgap reference[C]//IEEE Asia Pacific Conference on Circuits and Systems.Macao,China,2008:1204-1207.
[3]Ken U,Tetsuya H,Tetsuya A,et al.A 300 nW,15 ppm/℃,20 ppm/V CMOS voltage reference circuit consisting of subthreshold MOSFETs[J].IEEE Journal of Solid State Circuits,2009,44(7):2047-2054.
[4] Xing Xinpeng,Li Dongmei,Wang Zhihua.A near-1 V 10 ppm/℃ CMOS bandgap reference with curvature compensation[J].Journal of Semiconductors,2008,29(1):24-27.
[5] Leung K N,Mok P K T,Leung C Y.A 2-V 23-μA 5.3-ppm/℃ curvature-compensated CMOS bandgap voltage reference[J].IEEE Journal of Solid State Circuits,2003,38(3):561-564.
[6] Guan Xiaokang,Wang Xin,Wang A,et al.A 3 V 110 μW 3.1 ppm/℃ curvature-compensated CMOS bandgap reference[J].Analog Integrated Circuit and Signal Processing,2010,62(2):113-119.
[7] Fayomi C J B,Wirth G I,Achigui H F,et al.Sub 1 V CMOS bandgap reference design techniques:a survey[J].Analog Integrated Circuit and Signal Processing,2010,62(2):141-157.
[8]王红义,来新泉,李玉山,等.一种分段线性补偿的带隙基准[J].半导体学报,2004,25(7):771-777.Wang Hongyi,Lai Xinquan,Li Yushan,et al.A piecewise-linear compensated bandgap reference[J].Chinese Journal of Semiconductors,2004,25(7):771-777.(in Chinese)
[9]Li J H,Zhang X B,Yu M Y.A 1.2-V piecewise curvature-corrected bandgap reference in 0.5 μm CMOS process[J].IEEE Transactions on VLSI System,2010,18(1):1-5.
[10]Lam Y H,Ki W H.CMOS bandgap references with self-biased symmetrically matched current-voltage mirror and extension of sub-1-V design[J].IEEE Transactions on VLSI Systems,2010,18(6):857-865.
[11]吴志明,杨鹏,吕坚,等.非线性补偿的低温漂低功耗CMOS带隙基准源的设计[J].电子科技大学学报,2009,38(1):137-140.Wu Zhiming,Yang Peng,Lü Jian,et al.Design of low temperature drift and low power consumption CMOS bandgap reference with nonlinear compensation[J].Journal of University of Electronic Science and Technology of China,2009,38(1):137-140.(in Chinese)
