基于双耳互相关函数的声源定位算法

万新旺 吴镇扬

(东南大学信息科学与工程学院，南京 210096)

在机器人导航、助听器、人机接口、语音增强和盲源分离等领域，声源定位具有重要的作用.大部分定位算法采用麦克风阵，为了处理多路麦克风信号，该类算法需要较大的计算量.另一类是受生物启发的定位算法，该类算法使用2个麦克风模拟双耳的定位功能，具有计算量小的优点.

受生物启发的定位算法使用单耳谱线索和2种双耳线索:耳间时间差(interaural time difference，ITD)和耳间电平差(interaural level difference，ILD).ITD可以从双耳信号的互相关函数中提取，Calmes等［1］利用ITD信息来确定声源的方位;Kneip等［2］提出了一种利用ITD线索和耳间轴运动信息的定位算法;Raspaud等［3］利用 ITD和ILD定位;Li和Levinson［4］提出了一种基于 Bayes准则的定位算法，该算法使用了ITD，ILD和单耳谱信息.近年来，MacDonald［5］提出了一种互通道(cross-channel)定位算法，该算法等价于同时利用双耳线索以及单耳谱线索.互通道定位算法直接利用与头相关脉冲响应(head-related impulse response，HRIR)确定声源的方位.

本文提出一种利用双耳互相关函数(binaural cross-correlation functions，BCCF)的定位算法.通过将信号的BCCF与所有方位的双耳HRIR的BCCF相比较来确定声源的方位.实验结果表明，与互通道定位算法相比较，本文算法具有更好的定位性能.

1 信号模型

在人工头的左耳和右耳中各放置1个麦克风，左耳中麦克风接收到的信号xl(n)与右耳中麦克风接收到的信号xr(n)可表示为

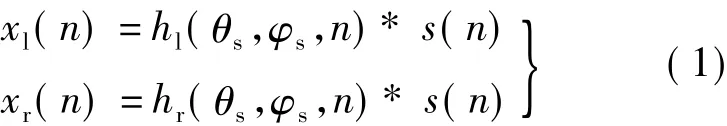
式中，“* ”表示卷积;s(n)为声源信号;θs和 φs分别为声源的方位角和仰角;hl(θs，φs，n)和 hr(θs，φs，n)分别为左耳和右耳的HRIR，HRIR是在声源信号已知的情况下通过测量得到的.

对式(1)作傅里叶变换，可得到频域信号模型为

式中，Xl(ω)，Xr(ω)和 S(ω)分别为 xl(n)，xr(n)和 s(n)的傅里叶变换;Hl(θs，φs，ω)和 Hr(θs，φs，ω)为与头相关传递函数(head-related transfer function，HRTF)，分别是 hl(θs，φs，n)和 hr(θs，φs，n)的傅里叶变换.

2 双耳互相关函数定位算法

首先计算双耳信号xl(n)与xr(n)之间的广义互相关函数(GCC)［6］.由双耳信号互功率谱的傅里叶反变换，可计算出GCC，即

式中，τ为时延;Ψl，r(ω)为频域加权函数.不同的权函数Ψl，r(ω)就有不同的GCC方法.当权函数为

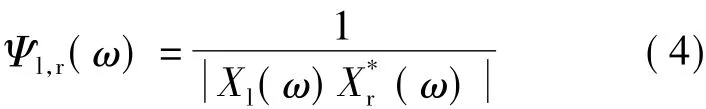
即用相位变换(phase transform，PHAT)加权时，GCC方法称作 GCC-PHAT方法.将 GCC-PHAT方法得到的广义互相关函数作为双耳互相关函数，即把式(4)代入式(3)，可得

利用频域信号模型，把式(2)代入式(5)可得

式中，RHlHr(θs，φs，τ)为由左耳和右耳的 HRTF 得到的双耳互相关函数.

由式(6)可知，双耳信号xl(n)与xr(n)之间的BCCF与声源所在方位的双耳HRIR的BCCF是相等的.由此，本文提出一种声源定位方法，该方法包括2个阶段:离线阶段和在线阶段.

1)离线阶段

由测量得到的HRIR数据库，计算所有方位的双耳HRIR的BCCF，即

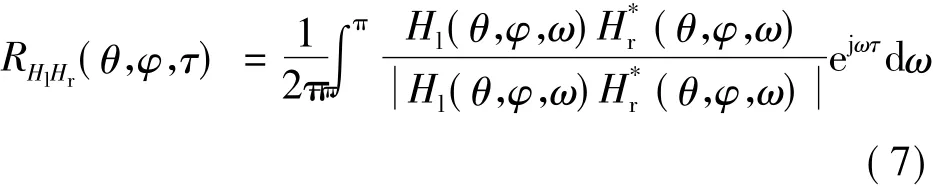
然后，存储所有方位的双耳HRIR的BCCF用于在线阶段的声源定位.

2)在线阶段

①双耳接收到信号后，由式(5)计算双耳信号的BCCF;

②计算双耳信号的BCCF与所有方位的双耳HRIR的BCCF之间的Pearson相关系数r(θ，φ);

③ 将最大的Pearson相关系数r(θ，φ)对应的方位作为估计的声源方位()，即

3 性能比较

为了验证算法的有效性，比较了基于双耳互相关函数定位算法与互通道定位算法的定位性能.

3.1 互通道定位算法

MacDonald提出了互通道定位算法，该算法也包含离线阶段和在线阶段.

1)离线阶段

测量得到HRIR数据库，存储所有方位的双耳HRIR用于在线阶段的声源定位.

2)在线阶段

① 双耳接收到信号后，对于所有方位(θ，φ)，将左耳信号xl(n)与右耳的HRIR进行卷积，将右耳信号xl(n)与左耳的HRIR进行卷积，即

②计算yl(n)与yr(n)的Pearson相关系数r′(θ，φ);

③ 将最大的 Pearson相关系数 r′(θ，φ)对应的方位作为估计的声源方位()，即

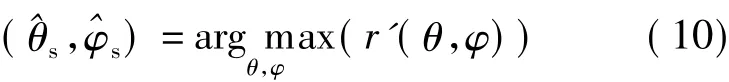
3.2 实验结果与分析

双耳信号由语音信号与双耳HRIR卷积产生.HRIR用配置了大耳廓的人工头录取，采样率为44.1 kHz，该HRIR数据取自CIPIC的HRIR数据库［7］.在以下的实验中，HRIR被降采样为16 kHz.

将2个采样率为16 kHz的语音信号作为声源，如图1所示，这2个声源信号只有很少的静音段.2个声源同时位于人工头的前半个水平面，人工头中的麦克风接收到的2个声源信号的能量相等，若以一个声源为信号，则另一个声源为有方向性的噪声，因而信号与有方向性噪声之间的信噪比为0 dB;同时加上无方向性的白噪声，使得信号与无方向性噪声之间的信噪比为15 dB.逐帧处理双耳接收到的信号，帧长为512个采样点(32 ms)，每帧加汉宁窗后用于估计BCCF，在以下的实验中，BCCF中的时延τ的取值范围为－2.5 ms≤τ≤2.5 ms.

图1 2个语音信号的波形图

图2给出了互通道与BCCF 2种算法的部分定位结果(2个声源分别位于－30°和30°).人工头的正前方对应的方位角为0°，左耳对应的方位角为－90°，右耳对应的方位角为90°.2个声源的方位角分别为－30°和30°，如图中虚线所示.2种算法的绝大部分主峰都近似指示了声源1或声源2的方位.对于互通道算法，大部分次峰都偏离了2个声源的方位;然而对于BCCF算法，大部分次峰仍然近似指示了声源1或声源2的方位.

为了评价算法的性能，采用了方位估计成功率和均方根误差2种性能指标［8］.对于每帧信号，若主(次)峰对应的方位角与声源的方位角之差小于20°，则该帧的主(次)峰方位估计是成功的.成功的方位估计次数与总的方位估计次数之比就是方位估计成功率.由于2个声源信号只有很少的静音段，因而所有帧的方位估计结果都用于计算均方根误差.

图2 互通道算法与BCCF算法的30帧定位结果

2个声源分别位于12种不同的方位，(θs1，θs2)∈ {( －20°，20°)，( －25°，25°)，( －30°，30°)，( － 35°，35°)，( － 40°，40°)，( － 45°，45°)，( －50°，50°)，( － 55°，55°)，( － 60°，60°)，( －65°，65°)，( － 70°，70°)，( － 75°，75°)}.图3给出了互通道算法与BCCF算法的主峰的成功率和均方根误差，横坐标给出了声源2的方位角，2种算法主峰的定位成功率都很高.图4给出了互通道算法与BCCF算法的次峰的成功率和均方根误差.可见在绝大部分方位，BCCF算法的次峰成功率比互通道算法高许多;BCCF算法的次峰均方根误差比互通道算法低.

为了更直观地评价互通道算法与BCCF算法的定位性能，将声源位于12种不同方位情况下的定位结果进行平均，定位结果的平均值如表1所示.可见，2种算法的主峰成功率都很高，BCCF算法的主峰成功率高出互通道算法约1.64%，BCCF算法的次峰成功率高出互通道算法约26.48%.

表1 主峰和次峰的成功率和均方根误差的平均值

图3 互通道算法与BCCF算法主峰的成功率和均方根误差

图4 互通道算法与BCCF算法次峰的成功率和均方根误差

4 结语

本文提出了一种利用双耳互相关函数的定位算法.首先利用HRIR数据库求出所有方位的BCCF，然后存储所有方位的双耳HRIR的BCCF用于在线阶段的声源定位.在定位阶段，先求出信号的BCCF，然后将其与所有方位的双耳HRIR的BCCF相比较来确定声源的方位.实验结果表明，在有2个声源同时存在的情况下，与互通道定位算法相比较，本文算法的主峰定位成功率提高了约1.64%，次峰定位成功率提高了约26.48%.

References)

［1］Calmes L，Lakemeyer G，Wagner H.Azimuthal sound localization using coincidence of timing across frequency on a robotic platform［J］.Journal of the Acoustical Society of America，2007，121(4):2034-2048.

［2］ Kneip L，Baumann C.Binaural model for artificial spatial sound localization based on interaural time delays and movements of the interaural axis［J］.Journal of the Acoustical Society of America，2008，124(5):3108-3119.

［3］ Raspaud M，Viste H，Evangelista G，et al.Binaural source localization by joint estimation of ILD and ITD［J］.IEEE Transactions on Audio Speech and Language Processing，2010，18(1):68-77.

［4］ Li D F，Levinson S E.A Bayes-rule based hierarchical system for binaural sound source localization［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing.Hong Kong，China，2003:521-524.

［5］ MacDonald J A.A localization algorithm based on head-related transfer functions［J］.Journal of the Acoustical Society of America，2008，123(6):4290-4296.

［6］Knapp C，Carter G.The generalized correlation method for estimation of time delay［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1976，24(4):320-327.

［7］ Algazi V R，Duda R O，Thompson D M，et al.The CIPIC HRTF database［C］//IEEE Workshop on the Applications of Signal Processing to Audio and Acoustics.New York，2001:99-102.

［8］Brutti A，Omologo M，Svaizer P.Localization of multiple speakers based on a two step acoustic map analysis［C］//IEEE International Conference on Acoustics，Speech and Signal Processing.Las Vegas，NV，USA，2008:4349-4352.