基于Markov链使用模型的加速统计测试方法

张德平 查日军

(1南京航空航天大学计算机科学与技术学院，南京 210016)

(2上海市计算机软件评测重点实验室，上海 201112)

(3东南大学计算机科学与工程学院，南京 210096)

软件测试过程中由于穷举测试工作量太大，实践上不可行，导致一切实际测试都不彻底，不能保证被测试程序中不存在软件错误.因此如何精选少量的测试用例对系统进行有效的测试，是软件测试研究中的关键问题［1］.目前，运用统计学原理指导测试用例的产生和选择，对测试数据进行统计分析的软件统计测试方法在理论上已经取得了很大进展，并在工程实践中取得了良好的效果［2-10］.

然而，对于高可靠软件特别是安全关键软件，其关键操作如紧急事故处理等操作，由于使用概率非常小，在基于使用的统计测试中往往得不到充分测试，而这类操作的可靠性要求往往很高，其失效会造成严重的后果.如果采用传统的统计测试方法，即使花费很长的测试时间也难以有效地对该安全关键软件实施充分的测试.因此，在软件测试过程中，如果能有针对性地暴露出对软件可靠性影响较大的软件缺陷，加速软件测试，将可以快速增加软件可靠性，还可显著减少软件测试开销.目前，国内外针对软件可靠性加速测试技术的研究还比较少［11］，因此有必要对其进行深入研究.

本文基于Markov链使用模型提出了一种加速统计测试方法，以软件总费用最小为目标，引入一种新的测试充分性判定准则来均衡测试成本与软件投放后的失效风险，利用交叉熵方法优化软件测试剖面，增加了关键操作的测试机会，加速了软件测试且降低了软件总费用.

1 基于费用的Markov链使用模型

Markov链使用模型是一个具有唯一初态和终态的Markov链，可用强连通有向图G=(V，A)和函数p:V×V→［0，1］表示，具有如下性质:

1)V={1，2，…，n}为节点集，表示软件系统的使用状态.

2)A为边集，其元素表示在某个状态下选定某个操作时软件状态间的转移.从状态i到状态j的边e定义为一个有序对(i，j)，任意2个状态i和j之间的一个方向最多只有一条有向边相连.

3) 转移概率 p(i，j)满足0≤p(i，j)≤1，表示从状态i一步转移到状态j的概率.整个软件系统状态之间的转移概率p(i，j)可用转移概率矩阵P表示，即 P=(p(i，j))n×n.

假定状态1为初态，状态n为终态，并且状态n为吸收态，它表示一旦进入状态n就不再离去，即 p(n，n)=1，p(n，j)=0，∀j≠n.每一个状态 i∈V都是从初态可达的，即在G中总存在一条从状态1到状态i的有向路径.每条边e均可估计出如下参数［10］:失效概率 f(e)，投放后的失效风险l(e)，测试成本c(e)，易知l(e)≫c(e).不失一般性，假定失效边在操作过程中总是失效，一旦经过测试，失效边均看作正确操作，不再造成软件失效.进一步假定［12］:

1)边(i，j)的每一次操作运行都有一个先验失效概率 f(i，j)≥0.

2)不同操作是否引起软件失效相互独立.

3)软件投入运行期间，失效边(i，j)至少历经一次，造成失效风险l(i，j)发生.

4)总失效风险由各边失效风险累加形成.

定义一个测试数据集 x={e1，e2，…，em}，ek∈A(k=1，2，…，m)为包含初态1和终态n的一个测试数据.根据规格说明书或用户实际使用生成测试数据集x的概率分布称为操作剖面，即转移概率矩阵P.边e可以在测试数据集x中出现多次，即测试数据集x中可以包含多条从初态1到终态n的路径.由假定可知，运行测试数据集x的测试成本为

测试前，每条边是否造成软件失效是不确定的，定义示性函数If(e)，对于给定的边e，如果测试过程中相对于边e的操作造成软件失效，则令If(e)=1，否则令 If(e)=0.显然，E［If(e)］=f(e).

假定软件投入运行后，软件失效均发生在平稳状态下.引入示性函数Ir(e)来描述过程是否达到平稳状态，即如果随机历经边e的状态是平稳状态时令Ir(e)=1，否则Ir(e)=0.由示性函数If(e)与Ir(e)定义知，它们相互独立.令¯A⊂A表示未经测试边的集合，由假设可知只有¯A中的边才可能因失效造成失效风险.则平稳状态下因未测试边失效造成的失效风险的期望可表示为

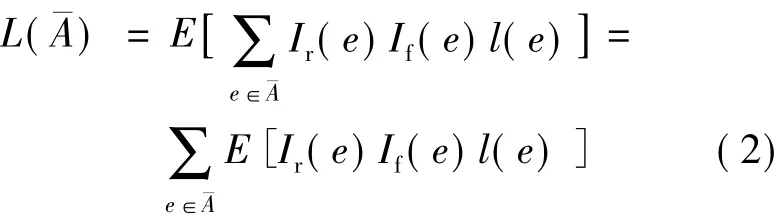
由If(e)与Ir(e)的独立性及期望的性质可得

式中，E［Ir(e)］=q(i，j)=q(e)为平稳状态下边 e=(i，j)被历经的概率.记πi为平稳状态下状态i(i=1，2，…，n)发生的概率，由 Markov过程转移概率与绝对概率之间的关系以及遍历性定理可知，平稳状态下边(i，j)被历经的概率为 q(i，j)=πip(i，j).

按照操作剖面P生成测试数据集x进行测试，当测试数据集足够大时，有可能测试完所有的边，使得¯A=∅，此时失效风险的期望L(¯A)=0.然而，随着测试数据集x边数的增长，相应的测试成本C(x)也会增加，因此软件测试停止时间取决于失效风险与测试成本的均衡.即生成测试数据集的最佳边数是使得软件总费用(失效风险与测试成本)最小时的边数.然而，这样生成测试数据集依然存在一个问题:小概率高风险的操作被测试到的可能性很小，生成的测试数据集并不一定是最佳测试数据集.为解决此问题，本文采用一种导向性启发式方法调节转移概率，确定一个最优(或近优)测试剖面(即测试中用来生成测试数据的概率分布)，然后根据最优测试剖面，均衡失效风险和测试成本生成最优(或近似最优)测试数据集.这类问题可归结为:确定一个最优测试剖面T*，根据T*生成测试数据集x使得期望软件总费用S(x)最小，即

式中，参数a说明失效风险相对于测试成本的重要程度，与合同、客户人数、市场信誉等因素有关，在实际应用中需要事先估计.

2 测试充分性准则

当测试资源不受约束时，统计测试按最优测试剖面选择边进行测试.测试初始阶段，测试成本随测试边数的增加而增加，而失效风险则随测试边数的增加而减少，并且由失效风险降低的费用要远比增加的测试成本多，因此软件总费用呈下降趋势;随着已测试边数的增加，失效风险降低速度减小，测试成本增加，测试一定数量的边后，软件总费用降到最低;随后，增加的测试成本多于失效风险减少的费用，软件总费用呈上升趋势.

记 S(xi－k)，S(xi)和 S(xi+k)分别表示测试数据集为 xi－k={e1，e2，…，ei－k}， xi={e1，e2，…，ei}和 xi+k={e1，e2，…，ei+k}时的软件总费用.由最优停止理论，统计测试的最优停止准则可采用一步向前看准则(1-stage look-ahead rule):令k=1，从初始状态出发，依据转移概率矩阵选取下一次操作(增加测试边)，如果满足

则在测试数据集中停止增加测试边，最佳测试数据集为xi.然而，在实际应用中由于选择测试边的测试剖面并不一定为最优测试剖面，相继选择的几条边并不一定能减少失效风险，这样可能会造成软件总费用有一个小的上升扰动后继续降低.为避免得到一个局部最优测试数据集，这里采用向前看k步准则(k-stage look-ahead rule).即对于给定正整数k，如果软件总费用满足

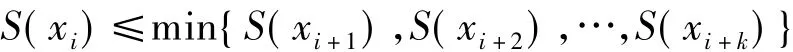
则在测试数据集中停止增加边，最佳测试数据集为xi.

3 加速统计测试技术

3.1 交叉熵方法

应用交叉熵方法［13］需解决的问题是:如何产生随机样本以及如何在每一次迭代中修正参数.

设x为根据转移概率矩阵P生成的一个测试数据集，则由Markov链的马氏性知测试数据集x出现的概率为

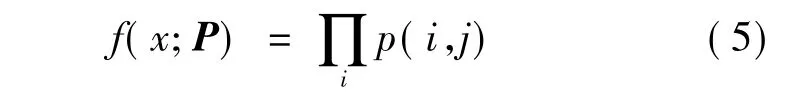
式中，i为测试数据集x中所有出现过的状态;j为依附边(i，j)∈A的状态.令γ*为失效风险S(x)在所有测试数据集组成的集合X中的最小值，则问题可改写为确定一个最佳转移概率矩阵(即测试剖面)，由此测试剖面生成测试数据集x*，使得

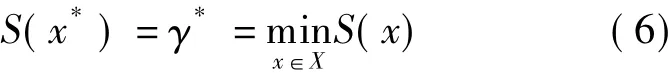
定义{I{S(x)≤γ}}为X上不同γ∈R值的示性函数集合，则式(6)中最优测试剖面确定问题可转化为如下概率估计问题来求解:

式中，Pu和Eu为相对于概率分布f(·;u)的概率测度和期望.

当γ=γ*时，l(γ)估计的最直接方法是采用重要抽样方法［14］:根据X上的概率分布g抽取样本 x1，x2，…，xN，则 l的估计为

显然，当概率分布g取

时只需抽取一个样本即可得l的一个方差为零的无偏估计.

从式(9)可看出，g*依赖于未知参数l，很难确定.因此一般在概率分布f(·;u)的概率分布簇{f(·;v)}中选取概率分布g来解决这个问题，即确定推断参数v使得f(·;v)与概率分布g*差别达到最小.常用来衡量2个概率分布差别大小的测度是K－L距离或交叉熵［13］.

这样，最优测试剖面的确定问题就转化为确定推断参数v，使得f(·;v)与概率分布g*的交叉熵最小，即

将式(9)代入式(10)可得如下等价推断参数确定形式:

由于测试数据集x={e1，e2，…}是根据转移概率矩阵P生成的，概率矩阵P可用推断参数v表示.测试数据集x的联合概率分布为

由拉格朗日乘子法，则式(11)的优化问题可转化为

式中，事件I{x∈Xij}表示测试数据集x在测试中历经状态i并从状态i转移到状态j.

由此可得最优测试剖面中不同状态之间的转移概率为

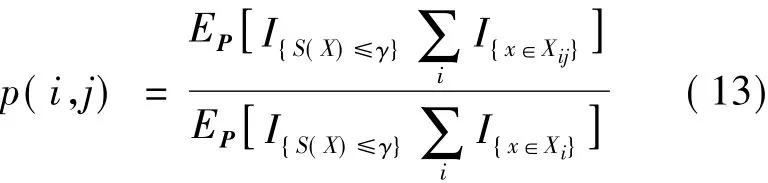
则最优测试剖面T*的每个转移概率的估计为

式(14)为不同状态之间转移概率的修正公式，其直观含义为:从状态i转移到状态j的概率为所有目标函数值(软件总费用)不大于γ的测试数据集中，从状态i一步转移到状态j的次数与测试历经状态i的次数之比.由此可知，在每一个状态中参数(不同状态下的转移概率)修正都是选用最有利于接近最优目标的“精英”测试数据集来修正.这样修正后使得下一次生成的测试数据集更接近于最优测试数据集，该机制使得每个状态的最优转移概率很容易找到，最终得到最优测试剖面，加速统计测试.

3.2 应用交叉熵方法加速统计测试

在基于Markov链使用模型的统计测试中应用交叉熵方法，可以由一个两步迭代过程实现:

① 适应修正 γt.对于固定的 vt－1，令 γt为在参数vt－1下目标函数值序列S(x)的ρ·100%分位数.即 γt满足

式中，x～f(·;vt－1).最简单的估计是根据参数vt－1抽样出的测试数据集 x1，x2，…，xN计算出目标函数值S(x)，并将其按从小到大排列(S(1)≤S(2)≤…≤S(N))，最后用N个目标函数值中的第ρ·100%个来估计γt，即^γt=S［ρN］.

② 适应修正 vt.对于固定的 γt和 vt－1，由式(14)得到修正的 ~vt，并采用平滑技术得到vt的修正值［13］:

步骤②中采用平滑技术主要是为了避免^vt的元素^vt，i取值为0，不能得到全局最优解.首次循环中，初始化转移概率矩阵为操作剖面P.由迭代过程可得^γ1和^v1，如此循环，可得序列对{(^γt，^vt)，t=1，2，…}.由文献［14］易知^γt→γ*，由此可得用于生成最优或近似最优测试数据集的测试剖面，具体算法如下.

算法1 最优测试剖面生成算法

① 初始化^v0为操作剖面P，令t=1.

② 根据参数^vt－1及相应的测试充分性判定准则自动生成随机测试数据集 x的样本 x1，x2，…，xN，计算各个测试数据集样本对应的目标函数值S(x)并排序 S(1)，S(2)，…，S(N)，找出 N 个目标函数值的ρ·100%分位数^γt=S［ρN］.

③ 用同样的测试数据集样本 x1，x2，…，xN，由式(14)解出~vt，应用式(15)的平滑技术得到 ^vt.

④令t=t+1，重复步骤②和③，直到满足停止条件.

⑤输出最优测试剖面.

测试数据集x1，x2，…，xN的自动生成过程可根据Markov过程性质及相应测试充分性判定准则运用蒙特卡罗方法来仿真生成，具体算法如下.

算法2 测试数据集的自动生成算法

输入:测试剖面T，各边失效概率，失效风险，测试成本.

输出:N个测试数据集及相应的目标函数值S(xi)，i=1，2，…，N.

For i=1 to N

初始化当前状态为初态1.

重复如下步骤，直到满足测试充分性准则:

①根据测试剖面T，在当前状态选取下一条边，若当前状态为终态，则下一状态为初态1;

②修改相应测试边的遍历次数及当前所在状态;

③计算目标函数样本值S(xi).

4 实例及灵敏度分析

4.1 实例分析

为了更好地说明利用交叉熵方法优化测试剖面的有效性，用一个列车调度信息系统软件［4-6，12-14］实例加以验证.图 1 给出了列车调度的Markov链使用模型.

图1 列车信息系统的Markov链使用模型

软件包括12个操作，每次执行从操作1开始，操作12是软件终止运行时执行的操作，边(8，9)和(8，10)导致关键操作9和10执行.假定每条边(i，j)的失效概率 f(i，j)、失效风险 l(i，j)和测试成本c(i，j)已估计出，如表1所示.

表1 马尔可夫使用模型中各边失效概率、失效风险和测试成本

失效风险重要程度参数a=105，每次迭代抽样的样本数N=1 000，ρ=0.02，d=4(或最大迭代步数为50)，平滑参数α=0.4，采用向前看30步停止准则生成最优测试剖面T*.分别根据最优测试T*和操作剖面P生成500个测试数据集.采用最优测试剖面T*时平均软件总费用为3 774，平均每个测试数据集遍历的边数为47;采用操作剖面P时平均最小软件总费用为8 983，平均每个测试用例集遍历的边数为22.两种情形下的平均失效风险、平均测试成本及平均软件总费用在测试边数增加时的变化曲线如图2和图3所示.

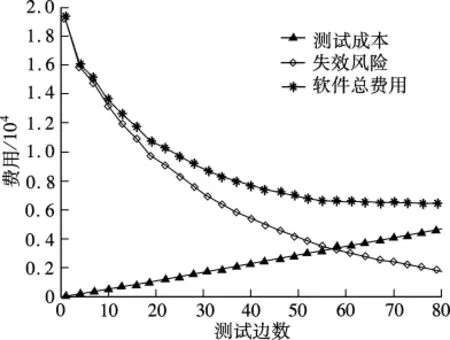
图2 采用最优测试剖面时的费用变化趋势

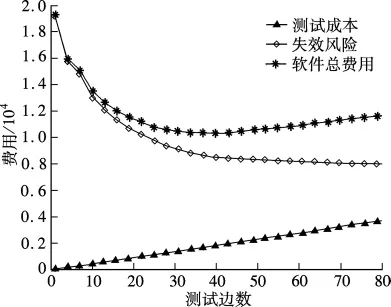
图3 采用操作剖面时的费用变化趋势

从图2和图3中可看出随着测试边数的增加，2种情形下平均失效风险都在降低并且下降速度逐渐变小，测试成本不断增加，软件总费用由高逐渐降低至最少，平均失效风险的减少量也逐渐变小.当平均失效风险减少量低于测试成本增加量时，软件总费用呈上升趋势，与前面的分析一致.采用最优测试剖面T*测试时平均失效风险下降的幅度要比采用操作剖面P时的大，平均软件总费用要比采用操作剖面时小.

图4和图5给出了按最优测试剖面和操作剖面分别生成的500个测试数据集中，各边累积遍历次数的柱状图.

图4 采用最优测试剖面时各测试边的遍历次数

图5 采用操作剖面时各测试边的遍历次数

采用操作剖面时，操作8被遍历的次数为53，关键操作9和10被遍历的次数分别为38和28.而采用最优测试剖面时，操作8被遍历的次数为761，关键操作9和10被遍历的次数分别为547和1 005.

4.2 灵敏度分析

为了研究算法1中各参数对测试效率的影响，采用向前看30步停止准则，d=4或最大迭代次数设定为50次，研究了在其他参数不变的情形下，100次仿真实验中参数α、迭代次数N和ρ分别变化时对平均软件总费用的影响.

实验1 参数α取值对总费用的影响

在参数ρ=0.01，N=1 000的情形下，α分别取0.3，0.4，…，0.9时，100次仿真试验的平均总费用变化曲线如图6所示.

图6 不同α取值下平均总费用变化曲线

从图6可看出，在其他参数保持不变的情形下，参数α在［0.3，0.9］之间取值时，对平均总费用没有显著的影响.在实际应用过程中，α值一般根据问题的复杂程度选取，如果问题复杂，不易收敛，则α值应偏大一些;若算法易收敛，则α值应偏小一些.

实验2 参数ρ取值对总费用的影响

在参数α=0.4，N=1 000的情形下，ρ分别取0.01，0.02，…，0.1时，100次仿真试验的平均总费用变化曲线如图7所示.

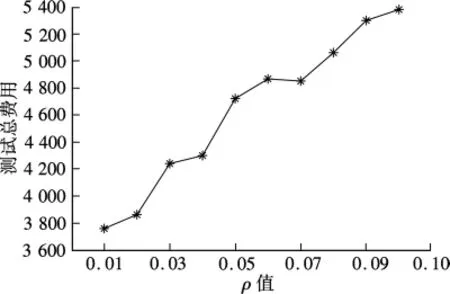
图7 不同ρ取值下平均总费用变化曲线

由图7可看出，在其他参数保持不变的情形下，参数ρ的取值较小时，平均总费用也较小，随着ρ的增加，平均总费用逐渐增加.其实质是在测试数据集的选择过程中，选择测试数据集的质量直接影响算法的性能.当测试数据集愈接近于最优测试数据集时，优化后的测试剖面更接近于最优测试剖面，这样经过多次迭代后得到的测试剖面就为最优(或近优)测试剖面.因此，对于参数ρ的选取应尽可能小，使参加测试剖面更新的样本适应值更接近于最优值.

实验3 参数N取值对总费用的影响

在参数α=0.4，ρ=0.01的情形下，样本容量N 分别取500，1 000，…，5 000时，100次仿真试验的平均总费用变化曲线如图8所示.

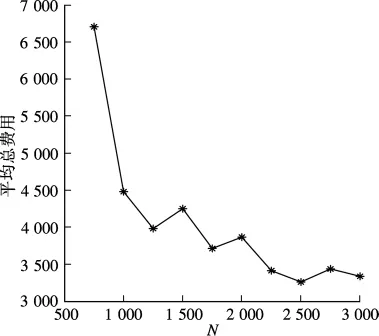
图8 样本容量对平均总费用的影响曲线

从图8可看出，在其他参数保持不变的情形下，随着样本容量N取值增加，平均总费用先急剧降低，然后趋于稳定.因此，参数N的选取应该在资源允许的前提下使测试数据个数最大.即如果能在每一次迭代中提高选择的测试数据集质量，就能达到提高算法收敛速度的目的.

5 结语

本文利用交叉熵方法通过一种修正机制调节操作剖面，增加小概率关键操作的测试机会，加速软件测试，在提高软件系统质量的同时降低软件总费用.应用软件加速统计测试技术需要确定某些参数值，如:边的失效率、失效风险和测试成本.实际使用中一般采用测试过程中得到的经验数据或通过专家经验进行估计，参数估计的精确性直接影响测试数据的有效性，如何利用测试过程中观察到的数据及以往经验数据对这些参数进行精确估计需作进一步研究.

References)

［1］陈火旺，王戟，董威.高可信软件工程技术［J］.电子学报，2003，31(12):1933-1938.Chen Huowang，Wang Ji，Dong Wei.High confidence software engineering technologies［J］.Acta Electronica Sinica，2003，31(12):1933－1938.(in Chinese)

［2］赵亮，王建民，孙家广.统计测试的软件可靠性保障能力研究［J］.软件学报，2008，19(6):1379-1385.Zhao Liang，Wang Jianmin，Sun Jiaguang.Study on the assurance ability of statistical test on software reliability［J］.Journal of Software，2008，19(6):1379-1385.(in Chinese)

［3］ Gutjahr W J.Failure risk estimation via Markov software usage models［C］//Proc 15th International Conference on Computer Safety，Reliability and Security.Vienna，Austria，1997:183-192.

［4］ Gutjahr W J.Importance sampling of test cases in Markovian software usage models［J］.Probability in the Engineering and Informational Sciences，1997，11:19-36.

［5］ Gutjahr W J.Software dependability evaluation based on Markov usage models［J］.Performance Evaluation，2000，40(4):199-222.

［6］ Doerner K，Laure E.High performance computing in the optimization of software test plans［J］.Optimization and Engineering，2002，3:67-87.

［7］ Doerner K，Gutjahr W J.Extracting test sequences from a Markov software usage model by ACO［C］//Genetic and Evolutionary Computation Conference.Chicago，IL，USA，2003:2465-2476.

［8］ Yan J，Zhou K P，Deng C H，et al.Importance sampling based safety-critical software statistical testing acceleration［C］//2010 International Conference on Computational Intelligence and Software Engineering.Wuhan，China，2010:1-4.

［9］徐云青，徐义峰，李舟军.基于使用模型的软件可靠性加速测试［J］.计算机应用与软件，2009，26(3):147-148.Xu Yunqing，Xu Yifeng，Li Zhoujun.Software reliability accelerated testing based on usage model［J］.Computer Applications and Software，2009，26(3):147-148.(in Chinese)

［10］张德平，聂长海，徐宝文.软件可靠性评估的重要抽样方法研究［J］.软件学报，2009，20(10):2859-2866.Zhang Deping，Nie Changhai，Xu Baowen.Importance sampling method of software reliability estimation［J］.Journal of Software，2009，20(10):2859-2866.(in Chinese)

［11］吴玉美，阮镰.软件可靠性加速测试的加速机理研究［J］.计算机应用，2006，26(6):1449-1551.Wu Yumei，Ruan Lian.Research on the acceleration principle of software reliability testing［J］.Computer Applications，2006，26(6):1449-1551.(in Chinese)

［12］张德平，聂长海，徐宝文.测试资源受约束的安全关键软件加速测试方法［J］.计算机科学，2009，36(5):138－141.Zhang Deping，Nie Changhai，Xu Baowen.Acceleration testing method of safety-critical software with testing resource constraint［J］.Computer Science，2009，36(5):138-141.(in Chinese)

［13］ Boer D P-T，Kroese D P，Mannor S et al.A tutorial on the cross-entropy method［J］.Annals of Operations Research，2005，134:19-67.

［14］ Margolin L.On the convergence of the cross-entropy method［J］.Annals of Operations Research，2005，134:201-214.