遗传算法综合智能天线的赋形波束

赵福玲 王永军 何绍林 聂贺峰

(中国电波传播研究所,山东 青岛 266107)

1.引 言

随着无线移动通信事业的飞速发展,人们对移动通信的需求也不断扩大。智能天线可以提高无线通信系统的性能,因此受到了广泛关注。智能天线技术是一种构建在天线设计和信号处理技术基础之上的综合技术。它能够实时地感知空间信号环境的变化,从而动态地优化接收或发送波束,以求达到最佳的信号接收性能。

自适应天线的波束赋形就是寻找可实现期望方向的阵列单元的激励幅相,而且获得的激励幅度应保证馈电网络易于实现。影响馈电网络耦合度的主要因素是阵列相邻单元的激励幅度之比。幅度越小,馈电网络的耦合度就越小,性能也就越好。

赋形波束的综合中,遗传算法具有很大的吸引力,它是一种全局优化技术。通过遗传算法,可以发现最优化的结果,或者是很接近最优结果的解。由于余割形赋形波束是一种具有低副瓣特性的窄波束,它可以在俯仰面内产生预先指定的赋形波束,在很宽的角域内有强度近于恒定的回波,能较好地满足用户的要求。因此,本文采用遗传算法进行综合智能天线的波束,使其具有余割波束。

2.智能天线及工作原理简介

自适应天线阵列,最初应用于雷达、声纳、军事方面,主要用来完成空间滤波和定位。在移动通信中普遍称为智能天线,确切的说应称为智能天线系统。因为智能的不是系统天线阵本身,而是天线和数字信号处理设备相结合的整个系统。

智能天线是一种能够根据信号环境的变化,实时地调整自身参数以进行最佳信号接收的阵列天线。

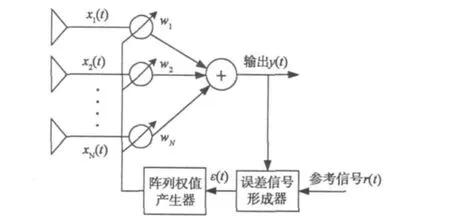
图1 自适应波束形成器原理图

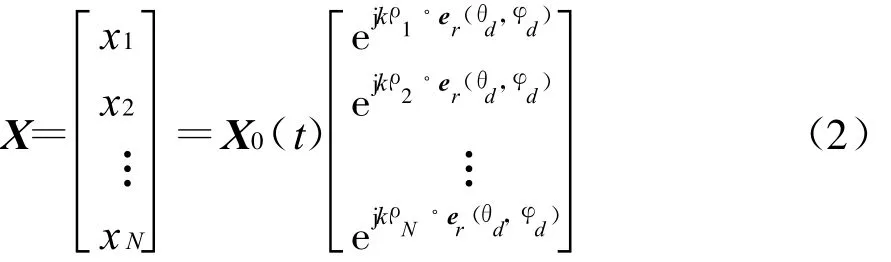
如图1所示,设有一个自由配置的N元阵,其阵元坐标用向径 ρi(i=1,2,…,N)表示。若从er(θd,φd)方向传来一个平面波,则在第i个阵元上的感应信号为

式中,X0(t)为坐标原点处来波信号。阵列响应可总体地用信号向量X表示为

若令bd

若各阵元响应的信号分别经过相应的加权 ω1、ω2、…、ωN后合成 ,则输出应为

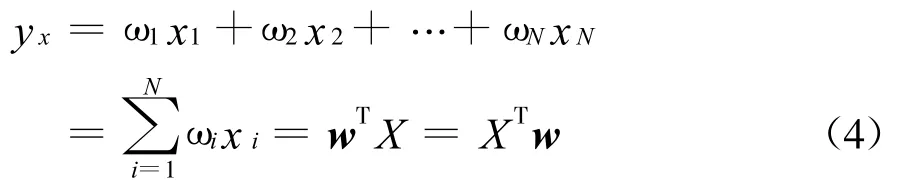
3.天线单元及阵列天线形式

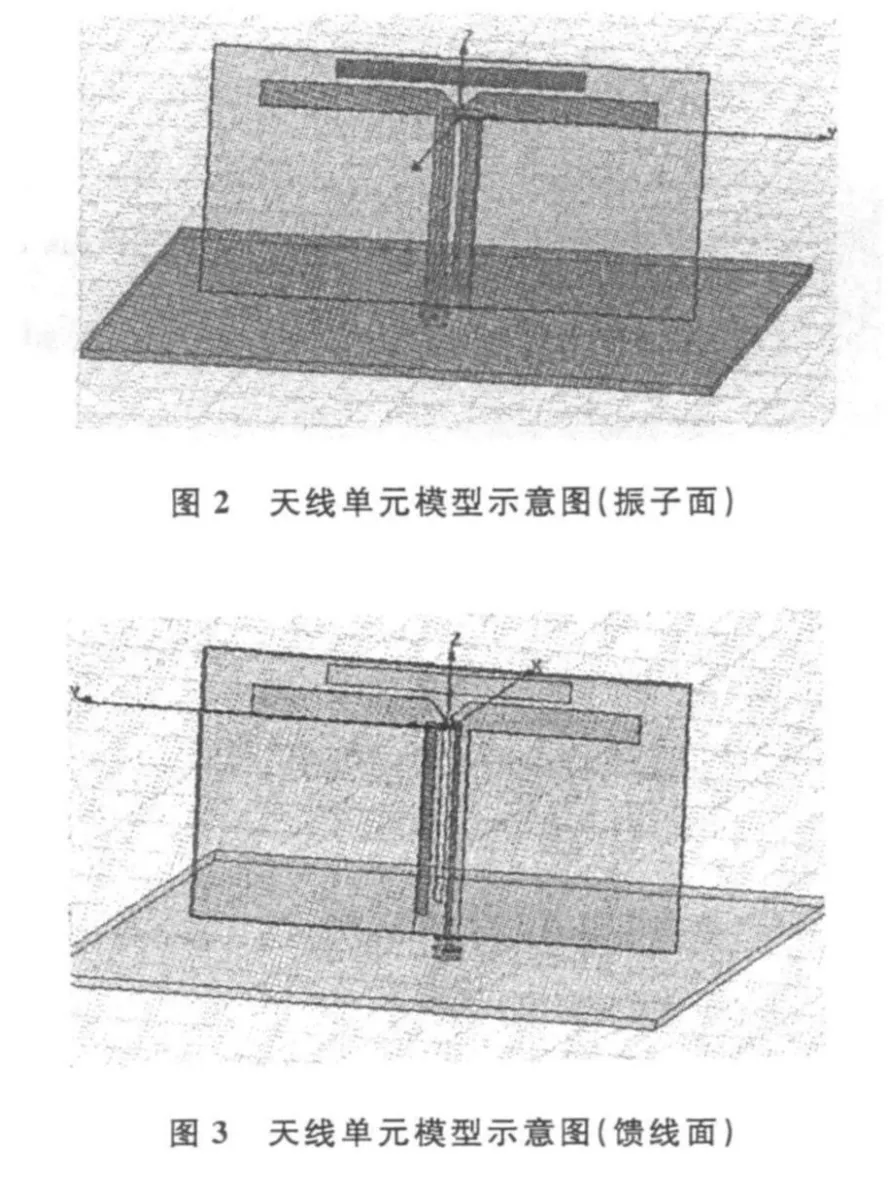
移动通信中最常用的天线单元形式是印刷振子天线,此类半波振子天线具有合适的频带宽度,印刷振子天线一致性好,厚度比较薄,方便加工,便于批量生产。通过在天线的下方加反射板的方法可以把振子天线的H面方向图压制成一个扇形波瓣形状。振子的馈电方式属于耦合馈电,振子和馈线由印制板的覆铜通过腐蚀形成,分布在电路板的两面,电流通过馈线耦合到振子上。由于馈电网络是非平衡结构,而天线需要平衡馈电,因而在馈电网络和天线之间应引入一个非平衡——平衡的巴伦。馈线采用倒J形带线馈电结构,该形式可以避免馈线谐振。由于弯曲形状振子臂的特殊形状,振子臂上的电流会使谐振频率往低频端偏移,振子天线单元的长度得到有效缩短。为了展宽频带和改善边频的方向性,在距离振子上部1.5 mm处增加了寄生单元。天线结构形式见图2和图3所示的天线模型。通过调整馈线、振子和寄生单元的尺寸与距离,振子天线单元的驻波系数小于1.5(归算于50欧姆)。

阵列天线采用间距为0.09 m的16个单元的自适应天线阵列,如图4所示。

图4 阵列天线示意图

4.仿真实例

本例采用间距为0.09 m的16个振子天线单元的自适应天线阵列,上边频为2.17 GHz,下边频为1.92 GHz.根据工程需要,需要设计一个天线方向图为绘制的类似余割形曲线的形式,利用读图软件得到每个变量和自变量的值。

采用遗传算法进行天线阵列综合计算优化得到类似余割形曲线形式的天线方向图。

遗传算法的运行过程为一个典型的迭代过程,简单遗传算法基本流程如图5所示,其必须完成的工作内容和基本步骤如下：

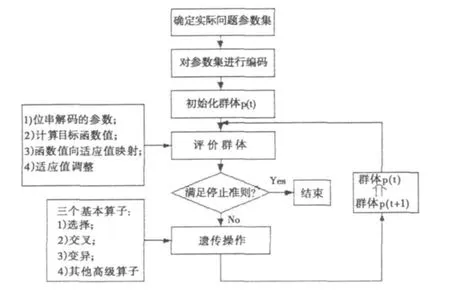
图5 简单遗传算法基本流程框图

1)选择编码策略,把参数集合X和域转换为位串结构空间S。

2)选择适应值函数f(X)

选择操作采用线性排序选择。排序选择的主要着眼点是个体适应度之间的大小关系,对个体适应度是否取正值或负值以及个体适应度之间的数值差异程度并无特别要求。所以不需要对适应度进行变换处理。本文中使用线性排序选择。线性排序的选择概率为

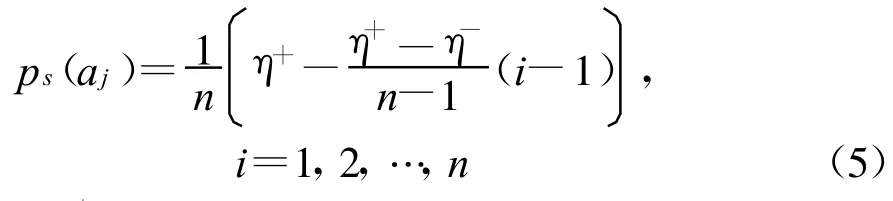
式中：η+为当前群体最佳个体a1在选择操作后的期望数量;η-为最差的个体an在选择操作后的期望数量;其他个体的期望数量按等差序列计算,即ηj=η+-Δη(i-1)=η+-(η+-η-)(i-1)/(n-1).

可以导出 η++η-=2。通过调节 η+和 η-的值,可以控制群体的选择压力。因此,这里根据进化的不同阶段,选择不同的 η+值。

3)确定遗传策略,包括选择群体大小n,选择、交叉、变异方法,以及确定交叉概率pc、变异概率p m等遗传参数。

4)随机初始化生成群体P。

5)计算群体中个体位串解码后的适应值f(X)。

6)按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代群体。

7)目标函数

由N个天线单元组成的均匀直线阵,阵列方向图表示为

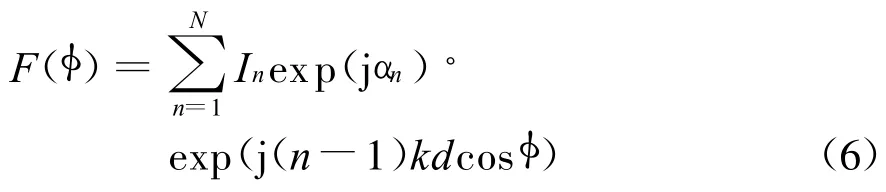
式中：In为第n个阵列单元的激励电流幅度;αn为第n个阵列单元的激励电流相位;d为阵元间距;k=2π/λ,λ为自由空间波长;φ为射线方向与阵列轴线之间的夹角。

当方向图不仅对主瓣赋形区的形状有要求,而且对副瓣电平和邻近电流比都有一定限制时,则使用罚函数法进行考虑。所以,最终的目标函数应包括三部分：一部分对应主瓣赋形区;一部分对应旁瓣区;一部分对应单元电流的动态范围。

8)判断群体性能是否满足某一指标,或者已完成预定迭代次数,不满足则返回步骤6),或者修改遗传策略再返回步骤6)。

本例遗传算法群体规模为n=300。由于在进化初期,染色体的差异一般较大,pc大和pm小有助于加快收敛;而在进化的中后期,pc小和pm大有助于防止过早陷入局部最优点。因此,交叉概率pc和变异pm概率随进化代数的变化关系表达式为

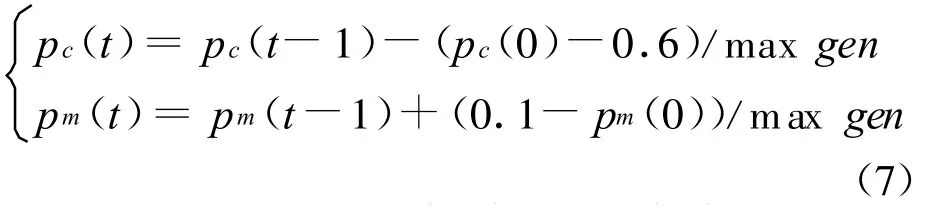
式中：初始交叉概率为pc(0)=0.8;初始变异概率为pm(0)=0.005;maxgen表示最大进化代数,设为1000。

通过遗传算法综合计算,得到优化波瓣赋形收敛曲线结果见图6。智能天线的三个频点(上边频、下边频、中心频率)上的波瓣优化结果见图7。智能天线遗传算法后阵列天线单元的幅度、相位的优化解见表1;阵列天线相邻单元的幅相对比见表2,实测波瓣的结果见图8。

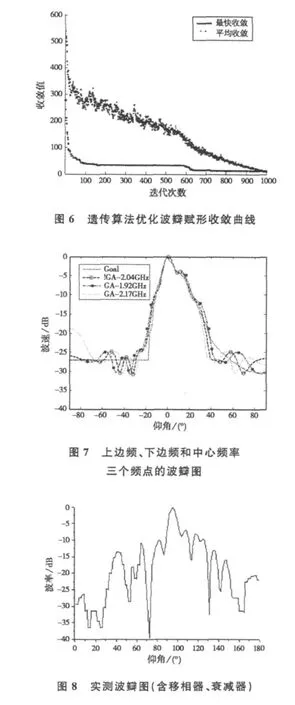
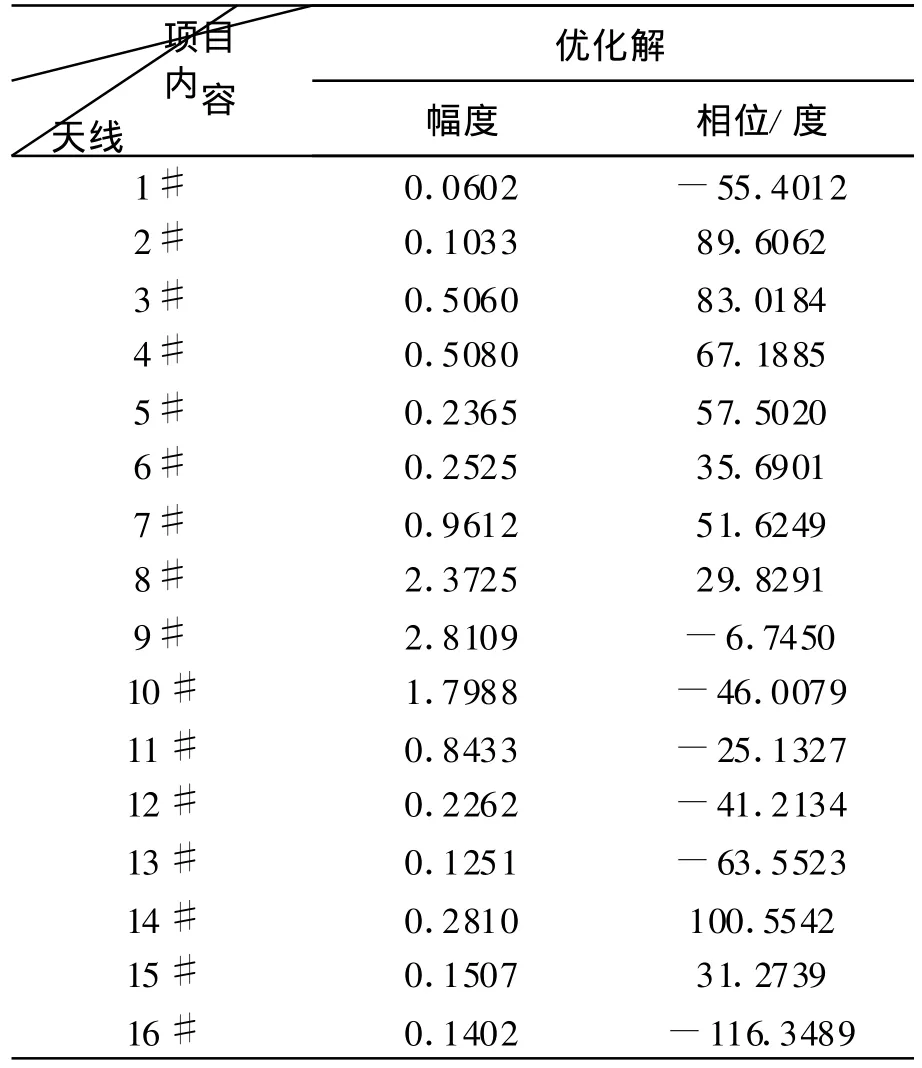
表1 阵列单元幅相的优化解

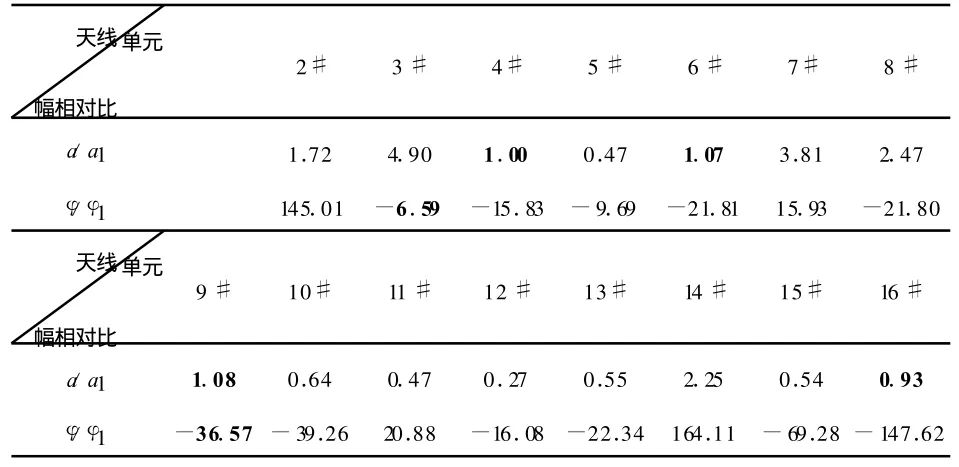
表2 相邻单元幅相对比

从图6可以看出,波瓣赋形的曲线具有很好的收敛性;从图7可以看出波瓣图很好地逼近了目标方向。图8实测数据可以看出,通过遗传算法综合的智能天线阵列波瓣图由于测试环境(楼顶,不是在微波暗室)、移相器和衰减器的不一致性及其加工误差等因素的影响,测试结果初步达到了预期的类似余割方向图。

5.结 论

应用遗传算法确定了阵列单元的激励幅度和相位,实现了余割赋形波束,且副瓣电平小于-15 dB,相邻电流幅度比有了明显的降低,从而易于馈电网络的实现。实测数据初步达到了预期效果,对智能天线的赋形波束具有工程指导意义,在工程实践中严格控制移相器、衰减器的一致性及其加工精度,使用该方法可得到比较满意的智能天线赋形波束。

[1] 杜志敏,薛 强,吴伟陵.智能天线技术简介[J].当代通信,2000,7(2)：38-40.

[2] 束咸荣,郭燕昌,晏焕强.阵列天线赋形波瓣权相位加权实现自适应零控[J].现代雷达,1998,20(2)：44-47.SHU Xianrong,GUO Yanchang,YAN Huanqiang.Adaptive null control in shaped patterns of array antennas[J].Modern Radar,1998,20(2)：44-47.(in Chinese)

[3] BOUKALOV A O and HAGGMAN S G.System aspects of smart antenna technology in cellular wireless communication-an overview[J].IEEE Trans.Microwave Theory and Techniques,2000,48(6)：919-929.

[4] SHEIKH K,GESBERT D,GORE D,et al.Smart antennas for broadband wireless access networks[J].IEEE Communication Magazine,1999,37(11)：100-105.

[5] THOMPSON JS,GRANT P M and MULGREW B.Smart antenna arrays for CDMA systems[J].IEEE Personal Communication,1996,3(5)：16-25.

[6] JOHNSON J M,RAHMAT-SAMII V.Genetic algorithms in engineering electromagnetics[J].IEEE Antennas and Propagation Magazine,1977,39(4)：7-21.

[7] SHAVIT R,LEVY S.Improved orchard-elliott pattern synthesis algorithm by peseudo-inverse technique and genetic algorithm[C]//IEEE Antennas and Propagation Society,AP-S International Symposium(Digest),2000：1042-1045.

[8] 石 镇.自适应天线原理[M].北京：国防工业出版社,1991：79-98.

[9] GODARA L C.Applications of antenna arrays to mobile communications,part i：performance improvement,feasibility,and system considerations[J].IEEE Proceedings,1997,85(7)：1031-1060.

[10] 李敏强,寇纪淞,林丹,等.遗传算法的基本理论应用[M].北京：科技出版社,2002：10-25.

[11] 舒 展,朱明富.基于遗传算法指纹分类在报关系统中的应用[J].计算机技术与发展,2006,16(11)：197-200.SHU Zhan,ZHU Mingfu.An application of fingerprint classification based on genetic algorithm in deposit boxes system[J].Computer Technology and Development,2006,16(11)：197-200.(in Chinese)

[12] 雷 娟,傅 光,杨 林,等.间接对称约束法设计阵列赋形波束[J].电波科学学报,2008,23(6)：66-70.LEI Juan,FU Guang,YANG Lin,et al.Synthesis of the array shaped beam using symmetrically and implicitly constrained method[J].Chinese Journal of Radio Science,2008,23(6)：66-70.(in Chinese)

[13] 孙艳丰,郑加齐,王德兴,等.基于遗传算法的约束优化方法评述[J].北方交通大学学报,2000,24(6)：14-19.SUN Yanfeng,ZHENG Jiaqi,WANG Deying,et al.A survey of constraint optimization method based on genetic algorithm[J].2000,24(6)：14-19.(in Chinese)