多用户直扩超宽带信号的码片宽度估计

张天骐 高永升 杜晓华 侯瑞玲

(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)

1.引 言

直扩超宽带(DS-UWB)信号采用极窄冲激脉冲和直接序列扩频(DS-SS)技术相结合以获得超宽频谱,其具有非常低的平均发射功率,这较大地增强了其安全性、低截获/检测概率(LPI/D),现在已广泛应用于民用和军事通信中。但非合作通信方要想对DS-UWB信号进行盲检测与估计,并获取所传输的信息就会变得异常困难,最好的办法就是先对DSUWB信号参数、扩频序列进行盲估计,再和主动通信一样获取所传输的信息。

目前,已报道的关于低信噪比DS-UWB信号盲检测与估计方面的研究较少,而且大多都是针对单用户DS-UWB信号。关于单用户DS-UWB信号盲检测的研究,文献[1]给出了希尔伯特—黄法、随机共振法、基于特征值分解法和分段相关累积(PACA)的检测方法。文献[2]利用循环平稳性进行了单用户DS-UWB信号的盲检测和参数估计。文献[3]通过小波的分解重构算法对UWB信号进行了不同分辨率级别上的时延估计。但是,针对多用户DSUWB信号的检测与盲估计研究却很少。

针对多用户DS-UWB信号的码片宽度估计问题,主要研究了多用户DS-UWB信号的特点及其循环谱密度函数,利用多用户DS-UWB信号循环谱的谱冗余特性,完成多用户DS-UWB信号的码片宽度估计。

2.多用户DS-UWB信号模型

所研究的超宽带(UWB)信号是指超宽带冲激无线电信号,以低占空比的超短冲激脉冲作为载体,采用DS-SS技术实现信息传输。首先,用PN序列对待发送的二进制符号序列进行扩频调制;其次,用窄脉冲进行脉冲幅度调制(PAM)。

在多用户DS-UWB系统中,第k个用户的信号波形可以写为

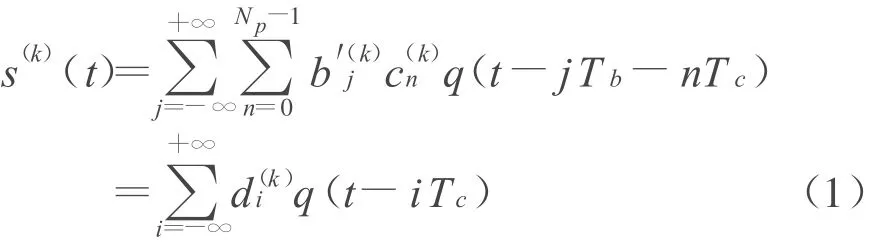
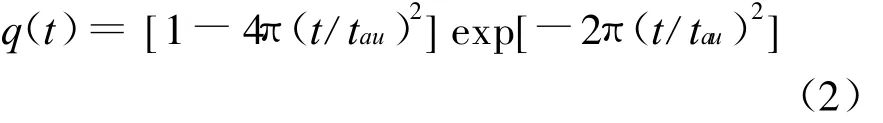
q(t)的傅立叶变换为

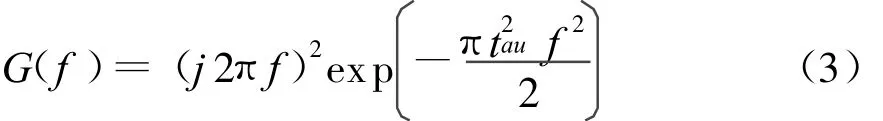
式中,tau称为脉冲形成因子,单位为秒,随着脉冲形成因子增大,二阶高斯脉冲波形变宽,但其能量谱密度的带宽变窄,选择符合超宽带信号的二阶高斯脉冲可通过选择合适的脉冲形成因子获得。注意到高斯脉冲的持续时间很长,这将不可避免地导致脉冲混叠和符号间干扰(ISI),因此,有必要对式(2)的高斯脉冲进行有效截断,截断长度的上限由不超过切普(chip)持续时间Tc决定,下限受产生极窄脉冲的技术水平限制,这里采用已经证明[Giancola 2002]的截断长度Tu,令Tu=1.1tau表示对高斯脉冲的有效截断,由此占空比可定义为Tu/Tc.

当系统中存在K个用户时,K个用户共用空间频谱资源,就产生了多用户干扰(MUI)。所有的分析都是基于以下假设：

1)所有信源产生二进制b序列,该序列由独立同分布且0和1等概出现的随机变量构成。

2)所有信源脉冲重复频率均为1/Tb.

3)信息码互相独立且等概率,每个码随机产生,且对应一个PN序列。

4)无线电信号在无多径影响的信道上传输,第n个用户与其参考接收机之间的无多径的信道冲激响应是路径增益Ak和传输时延τk的函数。传输时延是相互独立的,且在[0,Tb]上服从均匀分布。冲激响应表达式为 ：h(k)(t)=Akδ(t-τk),其中 δ(◦)为Dirac冲激函数。

5)信道的输出受到双边功率谱密度为N0/2(单位为W/Hz)的白噪声n(t)的污染。

因此,接收到的K个用户DS-UWB信号的波形为

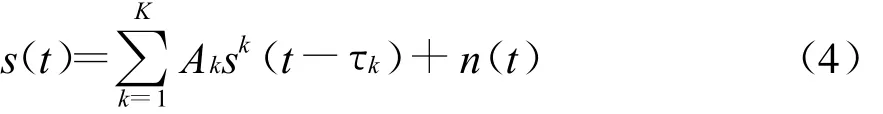
当 τ1=τ2= … =τk时,式(4)表示同步多用户DS-UWB系统;反之,称其为异步多用户DS-UWB系统。

3.算法原理

3.1 信号的循环平稳特性

周期平稳信号是一种特殊的非平稳信号,其具有周期平稳性,即其统计参数,如均值、相关函数等,都随着时间作周期性的变化。对于这种信号更适合建模为循环平稳随机过程,循环平稳随机过程可用循环谱密度函数来表征,该理论被称为循环谱理论或谱相关理论[5]。

假设x(t)是以T为周期的平稳过程,现将其自相关函数展开成傅氏级数,系数记为循环自相关函数(τ),得

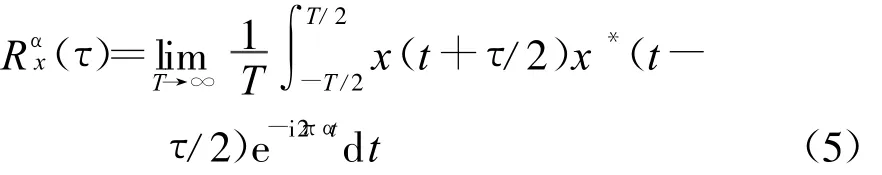
再对(τ)做傅氏变换,得到x(t)的循环谱密度函数(也称循环谱)为

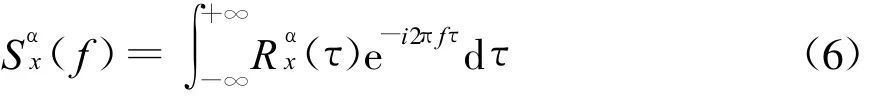
式中：α称为信号x(t)的循环频率,α=m/T(m是所有整数);f称为x(t)频谱频率。式(5)中(τ)是x(t)的两个复频移函数u(t)和v(t)的互相关函数,即

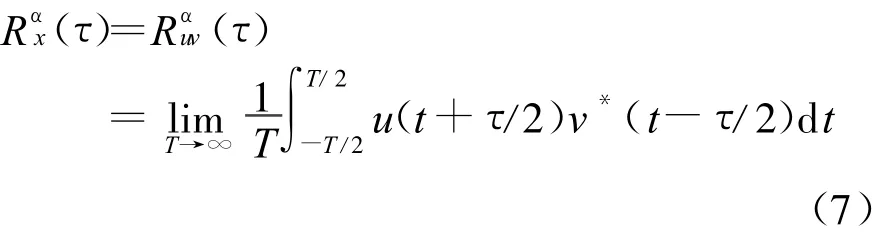
其中：

所以

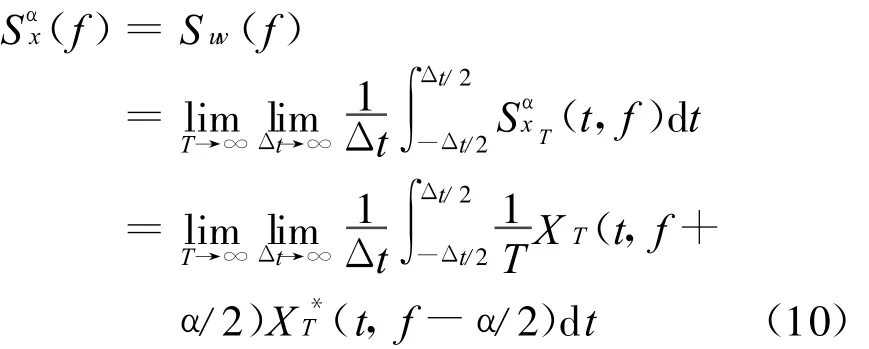
式中：

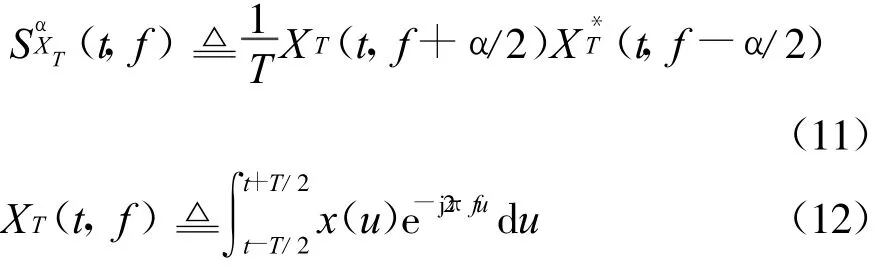
式(11)中(t,f)称为循环周期图。式(12)中XT(t,f)称为x(t)的短时傅立叶变换。从式(11)可知,循环谱密度函数(f)可表示为x(t)在频率f+α/2与f-α/2处谱分量间的互相关密度,因此,循环谱密度函数(f)又称为谱相关函数。

在循环相关检测和循环平稳信号的参数估计中,循环谱密度函数是一个重要的概念,能够完全表征循环平稳信号的很多特征。注意：实际上,循环平稳信号x(t)在频率f+α/2与f-α/2处谱分量是完全相关的,这种特殊的谱相关特性称为谱冗余,一般的平稳信号(包括高斯白噪声)就没有这种性质;利用谱冗余,可以从平稳的干扰中将循环平稳信号提取出来;不同的循环平稳信号具有不一样的循环频率α,可以利用不同的循环谱密度函数检测出不同的循环平稳信号。也就是说：平稳噪声和干扰在α≠0处不呈现谱相关,即(f)=0;而对于多用户DS-UWB信号,有α=m/Tc(m∈Z),Tc就是多用户DS-UWB信号的码片宽度,因此,利用谱冗余就可以完成码片宽度的估计。为方便计算,采用FFT Accumulation Method(FAM)算法[5]来对循环谱密度进行估计。

3.2 循环自相关和循环谱的叠加特性

在一个比较宽的带宽内,通常有许多信号和背景噪声,设接收信号c(t)由信号rl(t)(l=1,2,…,L)和噪声n(t)组成,即

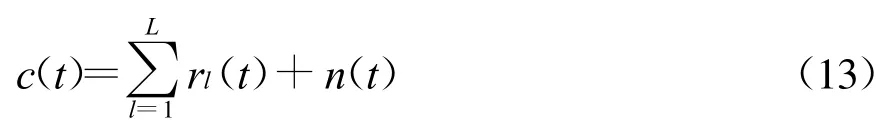
假设L个信号和噪声彼此统计独立,那么其循环自相关和循环谱满足叠加特性[7]

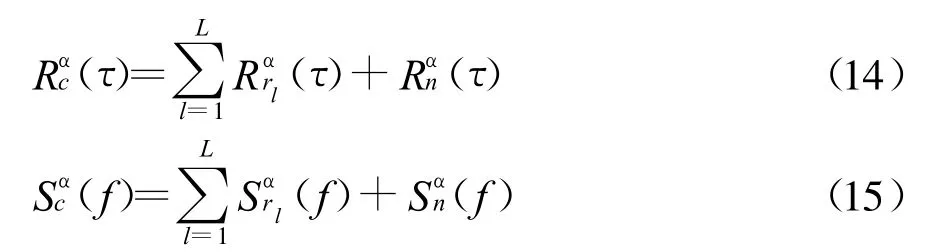
如果多个目标信号的循环频率彼此不同,背景噪声不是循环平稳的,就可以根据各自的循环频率进行检测、信号分离、参数(载频、符号率等)估计。特别地,如果只有一个信号,则c(t)=r(t)+n(t),其中n(t)是高斯白噪声,那么(τ)=(τ),(f)=(f).

3.3 多用户DS-UWB信号谱相关分析

为方便分析多用户DS-UWB信号的循环谱,首先研究单用户DS-UWB信号。由于噪声不具有循环平稳特性,为了简化运算,以下推导暂不考虑噪声的影响。单用户DS-UWB信号可视为一个特殊的脉冲幅度调制(PAM)信号,其采用宽度远小于码片(chip)宽度的二阶高斯脉冲进行调制。文献[7]已经给出了各种调制信号的循环谱密度函数。现在考虑单个用户的情况,系统接收到的第k个信号波形为

常见的调制系统可被模型化为一个以平稳过程为激励的多输入线性周期时变变换(LPTV)系统。所以,很容易用LPTV变化参数来研究信号的循环平稳特性。循环谱密度为的输入信号通过LPTV系统的输出循环谱密度为[7]

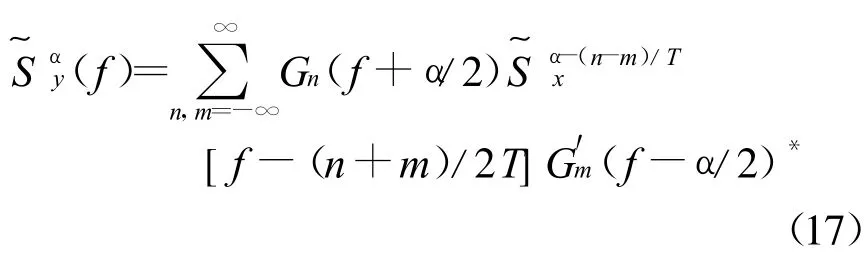
如果LPTV是时不变系统,上式简化为

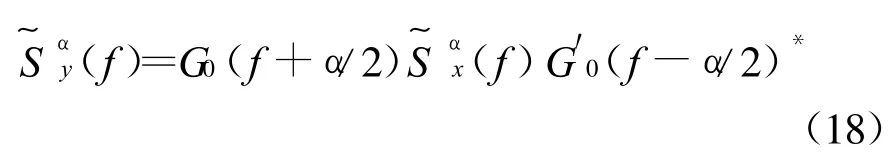
式中：α=m/T,T是LPTV系统的周期且T=Tc;Gn(f)和Gm(f)是冲激响应为h(t,u)的傅立叶级数的系数gn(τ)和gm(τ)的傅立叶变换。

首先考虑一般的幅度调制(AM),传统AM信号的模型为

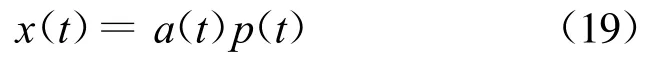
其中p(t)为载波,其傅立叶级数为

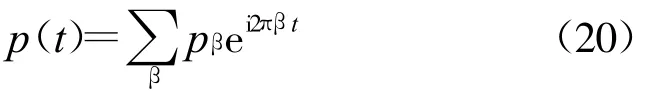
所以式(19)就可看成一个输入为a(t)的LPTV变换,其冲激响应的傅立叶级数系数为

式中,δ(τ)是Dirac冲激函数,且

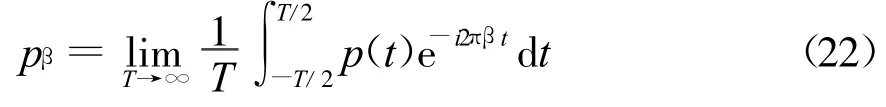
直接应用式(17)可以得到循环谱密度函数

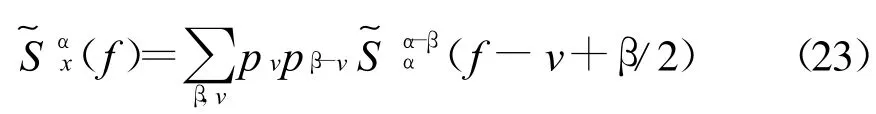
当

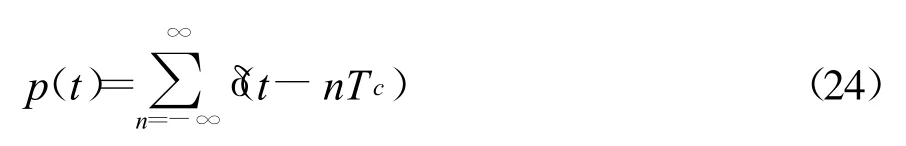
对所有的β=m/Tc,有pβ=1/Tc;利用式(23)得到循环谱密度函数为

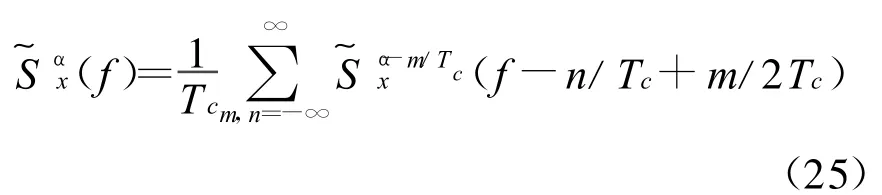
如果时间序列x(t)通过一个冲激响应为q(t)的滤波器,则y(t)=x(t)⊗q(t),y(t)就是PAM信号。将替代式(19)中的a(t),则式(16)可看作x(t)通过一个冲激响应为q(t)的LPTV系统的处理过程,根据式(17)就得到系统接收到的第k个用户信号的循环谱密度函数

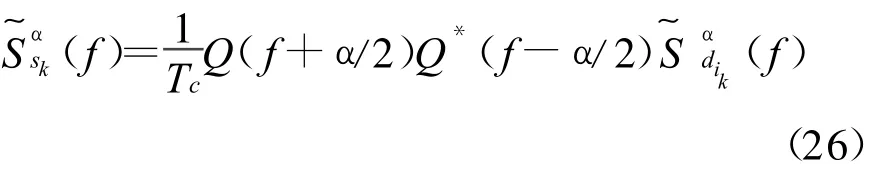
式中：

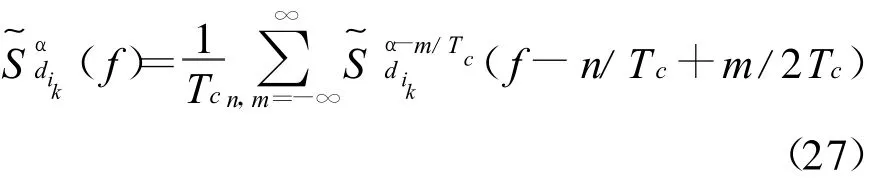
如果把信息序列和PN码序列调制的序列看作具有一般平稳特性[8],则有

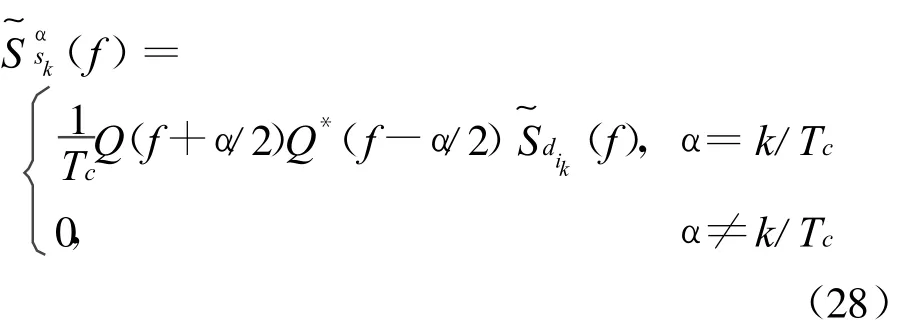
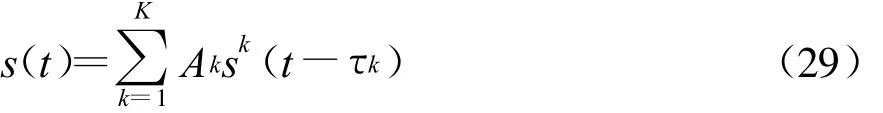
根据循环谱的叠加特性,多用户DS-UWB信号的循环谱密度函数为

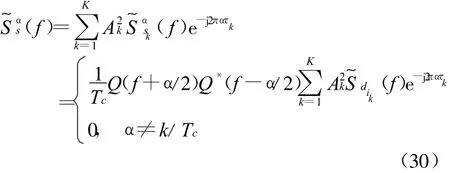
从式(30)可以看出：理论上多用户DS-UWB信号只是在单用户的基础上改变了谱相关函数的相位和幅度信息,并没有改变信号的循环频率和循环谱密度函数的谱相关特性。多用户DS-UWB信号(同步或者异步)仍然具有循环平稳性,循环频率就是码片宽度Tc的倒数的整数倍。多用户DS-UWB信号的循环谱密度将在α=m/Tc处产生谱线。因此,在某一频谱频率f处沿α轴搜索谱线间隔,码片宽度就能准确估计出来。

4.仿真实验

仿真实验1：

假设系统中有5个用户,并具有理想功率控制,且系统中各个用户的传输功率相同,Pow=-30 d Bm,采样频率fc=5×1010Hz,信息符号numbits=10 bit,码片宽度Tc=2.0×10-9s,脉冲成形因子tau=0.25×10-9s,每比特映射的脉冲数Ns=63位,PN码长Np=63位,高斯单周期脉冲冲击响应持续时间Tm=0.5×10-9s.加入零均值高斯白噪声,信噪比SNR=-10 d B.利用FAM算法计算多用户DS-UWB信号的循环谱密度,采样点数N′=12755,1/Δf的数据段内的离散傅立叶变换的点数N=32,Δt=12755Ts.通过计算机仿真可得到5个用户DS-UWB信号(同步和异步)的循环谱密度函数,其“循环频率α-频谱频率f-循环密度函数幅值”的局部放大图如图1和图2所示。

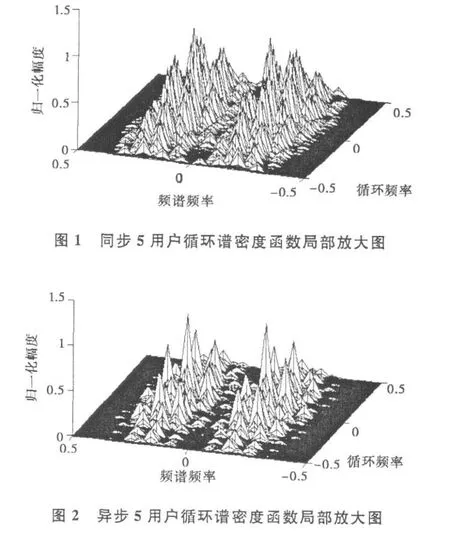
由于PAM调制脉冲q(t)不同于传统的矩形脉冲,所以多用户DS-UWB信号的循环谱密度函数与传统的PAM信号有所不同。从仿真结果可以看出：在f=0两边,多用户DS-UWB信号的循环谱密度函数出现两个对称的峰值,而不是在f=0处有单个峰值。

仿真实验2：

由式(30)可看出,多用户DS-UWB信号具有循环平稳性,其循环谱密度将在α=m/Tc处产生谱线。从图1和图2中发现：在某个频谱频率f的截面上,会出现一个幅度最大的谱线,在产生最大谱线的频谱频率fmax附近搜索次大谱线,两谱线之间的宽度就是估计的码片速率。图3和图4是fmax=7.815×109Hz的截面局部放大图。在仿真实验中,频谱频率fmax截面图只是截取了循环频率α=0正负5倍1/Tc的宽度,并且对所有的坐标进行了归一化处理,归一化频率f′max=0.1379。从图3和图4中可以看到,由于多用户之间干扰的存在,使得α≠k/Tc时出现类似噪声的干扰谱线,但是并没有改变信号的循环平稳性。比较图3和图4,同步情况下截面图中的谱线幅度大于异步的情况,说明异步多用户DS-UWB信号在α=m/Tc处的谱线更容易被噪声淹没。

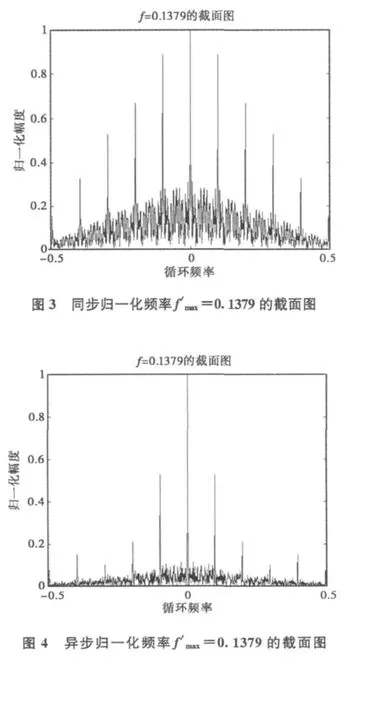
仿真实验中,经过搜索可得谱线之间的间隔ΔN=127,Δα=1/12755Ts=3.92 ×106Hz,码片速率1/Tc=ΔN/12755×Ts=4.9784×108bit/s,和真实值相差2.16×106bit/s,差值小于 Δα;估计值和真值之比为0.9957;估计的码片宽度T′c=2.0087×10-9s.由此可见,用此方法可以很好地估计多用户DS-UWB信号的码片宽度。

仿真实验3：

为进一步验证本算法的有效性及信噪比对估计性能的影响,在仿真实验2的基础上做M=400次的MonteCarlo仿真,得到(同步/异步情况下)要准确估计伪码宽度所需的累加次数随信噪比变化的曲线,如图5所示。

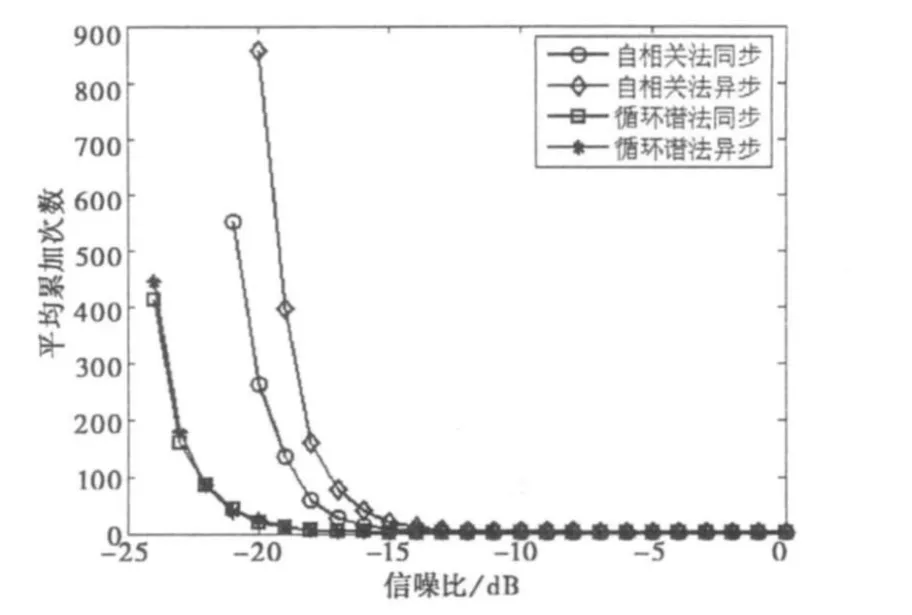
图5 两种算法下信噪比和平均累加次数的关系

从图5可以看出,同步多用户DS-UWB信号在-24 dB的信噪比下仍可准确估计码片宽度,异步多用户DS-UWB信号在相同条件下跟同步情况下的差别并不明显,同时所得到的最低信噪比容限比文献[2]中所得的单用户结果要小。同时,在同一信噪比下,异步多用户DS-UWB信号比同步多用户DS-UWB信号需要稍微多一点的累加次数才能准确地估计伪码宽度。由此可见,用此方法可在较低的信噪比下准确地估计多用户DS-UWB信号的码片宽度,且同步多用户DS-UWB信号的估计性能要略优于异步多用户DS-UWB信号。

另外,图5表明在进行多用户DS-UWB信号码片宽度估计时,循环谱算法所能达到的信噪比容限高于分段相关累积法所能达到的信噪比容限,估计性能比较好。但是在程序运行中,循环谱算法估计参数时需要更多的时间来完成,计算量比较大。

5.结 论

针对多用户DS-UWB信号模型,通过理论分析得到了多用户DS-UWB信号的循环谱密度函数。理论推导发现系统中改变用户数目的情况下,接收信号的循环谱密度函数仅仅在相位和幅度信息上改变,但信号的循环频率并不改变。所以,利用循环相关理论也可以完成多用户DS-UWB信号检测及其码片宽度估计。最后给出了仿真结果,验证了理论分析的结果且和分段相关累积法进行比较。从仿真结果看,用循环谱分析法估计多用户DS-UWB信号的码片宽度,可以在较低的信噪比下得到较好的估计效果,并且同步多用户DS-UWB信号的估计性能要略优于异步多用户DS-UWB信号;此算法的估计性能明显比分段相关累积法的估计性能好。

[1] 王明阳.非合作超宽带冲激无线电信号检测技术研究[D].2006,国防科学技术大学：信息与通信工程.

[2] 虞路勤,张天骐,李越雷,等.DS-UWB信号的谱相关分析及码片宽度估计[J].电视技术,2010,34(4)：56-59.YU Luqin,ZHANG Tianqi,LI Yuelei,et al.The analysis of spectral correlation of DS-UWB signal and estimation of chip interval[J].Video Engineering,2010,34(4)：56-59.(in Chinese)

[3] 陈隽永,徐 庆,徐继麟.超宽带雷达中基于小波变化的时延估计方法[J].电波科学学报,2001,16(2)：245-248 CHEN Juanyong,XU Qing,XU Jilin.A new timedelay estimation for the ultra wide-band radar[J].Chinese Journal of Radio Science,2001,16(2)：245-248.(in Chinese)

[4] 张天骐,苗 圃,马国宁,等.多径环境下的直扩信号伪码周期估计[J].电波科学学报,2009,24(5)：973-978.ZHANG Tianqi,MIAO Pu,MA Guoning,et al.Period estimation of the PN sequence for direct sequence spread spectrum in multipath environment[J].Chinese Journal of Radio Science,2009,24(5)：973-978.(in Chinese)

[5] GARDNER W A.Spectral correlation of modulated signals：part I-analog modulation[J].IEEE Transactions on Communication,1987,35(6)：584-594.

[6] 喻 凯.基于循环谱的MPSK信号盲参数估计[D].2007,电子科技大学：通信与信息工程.

[7] ROBERTS RS,BROWN W A,LOOMISH H,et al.Computationally efficient algorithms for cyclic spectral analysis[J].IEEE Signal Processing Magazine,1991,8(2)：38-49.

[8] 张天骐.DS及DS/CDMA信号的估计方法研究[D].2002,电子科技大学：电路与系统.

[9] 张天骐,周正中.直扩信号伪码周期的谱检测[J].电波科学学报,2001,16(4)：518-521.ZHANG Tianqi,ZHOU Zhengzhong.A new spectral method of periodic detection of PC sequence in lower SNRDS/SS signals[J].Chinese Journal of Radio Science,2001,16(4)：518-521.(in Chinese)

[10] GA RDNERW A.Exploitation of spestral redundancy in cyclostationary signals[J].IEEE Signal Processing Magazine.1991,8(2)：14-36.

[11] GARDNER W A.Measurement of spestral correlation[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1986,34(5)：1111-1123.