基于探测过程建模的探地雷达多目标识别
2011-08-08姬光荣姬婷婷
高 翔 姬光荣 姬婷婷 王 群
(1.中国海洋大学信息科学与工程学院电子系,山东青岛266100;2.国家深海基地管理中心,山东青岛266061;3.中国人民解放军总装工程兵研究一所,江苏无锡214035)
1.引 言
目前,全世界平均每年有2万余人因战后的未爆地雷致死或致残,地雷的探测与排除技术在国际上始终受到关注[1]。在现代地雷中,反步兵地雷等浅层目标的体积小、金属成分少,传统的金属探测器无能为力,而探地雷达(GPR)利用高频电磁波的发射与接收实现地下无损探测,具有更好的普适性,因此,得到了广泛应用[2]。
已有大量文献对GPR数据的杂波抑制与地下目标定位进行了讨论[3],本文在其基础上专注于利用目标区域的回波信号对埋藏目标进行识别。GPR信号的目标识别包含两方面关键内容:对回波信号进行有效的特征提取以及选取适合的判别算法对地下目标进行识别。在特征提取中,维格纳-威利(WVD)分布及其扩展[4-5]、S变换[6]、小波变换[7]以及功率谱估计[8]等非平稳随机信号处理方法被许多学者所关注,线性判别分析与主元分析等方法也有学者进行研究[7,9]。另一类思路针对B-scan图像中目标形成的双曲线,采用各种图像处理手段描述目标[10-14]。相比较而言,时频分析方法更贴近信号的本质特性,有利于进行分类识别。在目标识别中,神经网络[7,15]较好的并行计算和学习能力以及支持向量机(SVM)[16-17]较强的小样本推广能力使它们在GPR信号分析中已有成功的应用。此外,隐马尔可夫模型(HMM)也是报道较多的方法之一。目前国际上绝大部分HMM应用于GPR信号的讨论来自于Paul D.Gader领导的研究小组[11-14],但他们的HMM检测算法都以回波信号中双曲线目标的形状特征为基础,并未涉及信号中丰富的时频联合信息。
在探地雷达扫描过程中,天线沿水平方向移动并采集数据,在某特定位置收到的一维时域信号反映了此点下方铅直方向的地下介质分布状况,一般将此一维时域信号称为A扫描或A-scan;由若干A-scan并行组成的位置—深度二维数据称为B扫描或B-scan;由若干平行的B-scan组合形成的三维数据称为C-scan.A-scan是探地雷达回波信号的基本组成单元,而时频分析正是研究A-scan这类时域非平稳随机信号的优良工具。时频分析灵活性强、能够定量描述信号在时域和频域的能量分布特征。考虑到时频分析结果的二维特点,本文结合图像的纹理特征分析,提出采用纹理描述算子提取时频分析结果的特征,以便反映出A-scan序列的变化情况。在实际探测中,探地雷达天线与目标在空间上存在着“由远及近再及远”的变化过程,这种空间变化通过一系列A-scan组成的序列的变化得到表现。扫描过程中相邻的A-scan之间具有较强的相关性,因此,可将扫描过程得到的A-scan序列作为一个整体来建模。HMM的优势正在于其对变化过程进行建模的能力,即它能够定量描述对象在不同状态间转换并表现出来的过程,这一点是神经网络与SVM等仅利用特征点集进行分类的识别算法无法做到的。本文正是以HMM的这一特点为基础,利用A-scan的时频纹理描述算子构造特征量以反映探测回波的变化过程,结合探测实际采用无跨越单向连续HMM对变化过程建模,实现地下目标的识别。仿真实验证实了基于HMM算法的分类性能优于SVM.
2.基于时频分析纹理描述的特征提取
在时频分析中,由于短时傅里叶和小波变换等线性方法无法描述信号的瞬时功率谱密度,因此,本文采用双线性方法,以使结果更加直观和合理;对于包含时间窗的Cohen类分布,时间窗无疑限制了应用的灵活性,因此,本文采用不含时间窗的WVD分布对A-scan信号进行时频分析。同时,由于本文关注的是时频图像纹理间的区别而非信号内各分量间的干扰,因此,WVD分布的交叉项问题并不影响此处的应用。信号x(t)的WVD分布如式(1)所示
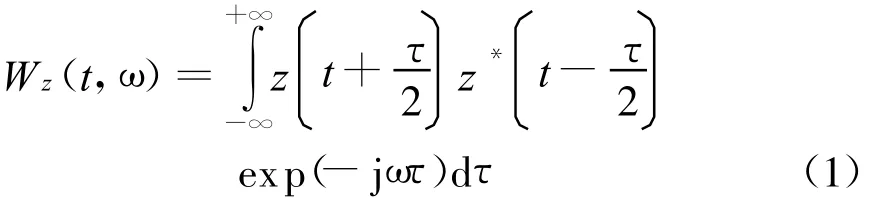
式中,z(t)是x(t)的解析信号。鉴于不同位置A-scan的WVD分布图像仅在某些特定时窗与频宽内显著变化,在得到WVD分布图像后采用文献[4]所述的3σ局部化算法提高计算效率。
一维时域信号经WVD分布可得到二维时域-频域联合分布图像,需在此基础上提取其特征。本文结合图像处理的有关内容,采用图像纹理分析方法进行特征提取,而纹理分析中选择合适的纹理描述算子构建特征向量是问题的关键。纹理描述算子的选取原则是使彼此具有尽可能小的相关性,以便全面反映信号特征。本文一方面借鉴了灰度共生矩阵(GLCM)[18]与纹理特征编码方法(TFCM)[19],在得到纹理特征编号共生矩阵(TFNCM)后,选取式(2)~(5)所述的4个描述算子;另一方面部分地吸收了Savelyev等人[4]的方法,采用WVD分布图像的第一奇异值和奇异向量作为描述算子,如式(6)~(7)所述。
1)能量指数或均匀度(EN)

2)四阶簇变形指数(CP)

3)二阶差分矩(SODM)

4)相关性指数(CO)

式中:pΔ(i,j|d,θ)表示当毗邻像素灰度差异阈值为 Δ时,方向角为θ、距离为d的TFNCM 矩阵中的(i,j)元素;μi和 μj表示给定(d,θ)下 TFNCM 矩阵中的行方向均值与列方向均值。d与θ的组合表示八个与中心像素的毗邻像素,纹理描述算子的最终结果取八个情况的均值即可。
5)第一奇异向量指数(FSVeI)

6)第一奇异值指数(FSVaI)

式(6)~(7)中:K与L分别为时频分析图像的时宽及频宽 ;σ1,σ2,u1,2与 ν1,2分别为最大和次大奇异值及其对应的奇异向量。
3.基于HMM的目标识别
HMM起源于20世纪60年代后期,是一种描述随机过程统计特性的参数化方法。HMM的显著特点是双重随机性:马尔可夫链用来描述随机状态转移,而一般随机过程用来描述某状态的随机观察序列,两类随机问题均采用概率密度函数进行描述。模型中的状态转移过程不可见,固称之为“隐”马尔可夫模型。HMM 用以下参数表征:λ=(A,B,π),其中A为状态转移概率矩阵,B为观察序列概率矩阵,π为模型初始状态。
若状态总数为N,状态序列Q={qt},则A=[aij]且aij=P(qt=j|qt-1=i)其中i,j=1,…,N.在实际探测中,探测天线与地下目标之间存在着“由远及近再由近及远”的变化过程,如图1所示。考虑到尽可能使模型简化、减小计算量,本文采用无跨越单向HMM建模。根据上述距离变化的物理意义,可取隐状态个数N=3,状态集合为{“远离”,“接近”,“远离”},状态间彼此互不相同且只能单向切换,状态转换如图2所示。关于隐状态个数N的确定,实验部分将进一步讨论。

本文的可观测符号为连续值的时频纹理特征向量,因此使用连续HMM建模。在探测范围内,设观察序列为正态分布且概率密度函数各不相同,对于任意位置的A-scan,其观察序列概率可采用高斯混合模型(GMM)描述,采用一个或若干个高斯函数分量的线性相加来表征总概率。记观察序列概率矩阵B=[bj(ot)],其中

式中:M为GMM中高斯分量的个数;ot为前述的6维特征向量;μj(m)为第j个状态下第m个高斯分量的均值;为相应的协方差;ωj(m)为混合权值,且若每个观察序列的长度为T,则有为6维高斯函数


模型初始状态可取“远离状态”;A的各行元素均匀取值即可,且满足;对于矩阵B,将训练集观察序列中的特征向量根据三类状态进行3-均值聚类,计算每个聚类的均值、方差及归一化权重,得到初始的高斯混合模型。
在训练过程中,首先将数据归一化,再采用Baum-Welch算法估计模型参数。考虑到实际计算中的下溢问题,加入比例因子项。记α为前向概率,β为后向概率,则

比例因子由下式计算

则前向概率计算公式改写为

后向概率为

由此,状态转移概率矩阵A的重估公式为

式中:

式中,k表示第k个观察序列,1≤k≤K.对矩阵B的重估转化为对混合高斯概率密度函数的重估,三个参数的重估公式分别为


另外,在利用Viterbi算法选择最佳状态序列时,为了避免使用比例因子,采用对数形式对概率进行计算[20]。
在识别环节,在数据归一化后,对于每个训练得到的HMM采用Viterbi算法[20]计算其产生待识别序列的概率,取最大者作为识别结果。
4.实验结果与分析
本文所用数据来自比利时皇家军事学院超宽带探地雷达实验室[21],埋地目标为PMN地雷、VS/50地雷、PRB409地雷、石块4类物体。数据共包含18组C-scan,分别在不同目标、不同土壤介质类型与不同埋藏深度的状况下获得,每组C-scan包含50×50组A-scan。本文对包含埋藏目标的17组C-scan进行训练与识别。对于每一组C-scan,本文取目标周围平行于扫描方向的26个B-scan(第15道至第40道)作为训练与测试数据,如图3所示,图中深灰色为埋地目标,浅灰色区域为本实验所用数据区,箭头所指为扫描方向。

图3 实验数据空间分布示意图
在基于HMM的识别过程中,对于扫描沿径B-scan中的每一条A-scan,首先计算其WVD分布,再对结果进行时频纹理特征提取,形成6维特征向量,将每一道B-scan转化为长度为50的特征向量观测序列,以26个观测序列为基本单位对其相应类别进行训练并识别。在得到特征向量后,本文采用文献[17]所述基于SVM的识别方法作为对比,在交叉验证选取参数后,先采用基于单通道的SVM识别方法进行计算,再将扫描沿径上的每一道B-scan作为多通道输入,以提高准确率。
考虑到训练数据与测试数据的选取对识别结果影响较大,本文针对训练充分和训练不充分两种情况进行实验。实验方案Ⅰ(训练不充分情况):将第15~30道B-scan作为训练集,共16×17=272组观测序列,分为17类,分别对SVM与HMM两个模型进行训练并测试;将第31~40道共10×7=170组观测序列作为测试集进行测试。此方案中训练集与测试集所用数据相对目标位置完全不同,两组数据包含不同信息,可看作训练不充分情况下的测试。实验方案Ⅱ(训练集充分情况):将第15~40道中的奇数道作为训练集,偶数道作为测试集,两组数据各有13×17=221组观测序列。此方案中训练集与测试集所涉及数据位置相似且完全覆盖目标,包含信息相似,可看作训练充分情况下的测试。
按照上述两个实验方案,可得表1和表2所示结果,可以看出:训练不充分方案的识别率明显低于训练充分方案;在利用训练集生成模型后,模型对训练集的识别率也必然高于测试集。
表1显示了SVM与隐含状态个数为3的HMM的识别结果对比,其中每个状态GMM中的高斯分量个数M的取值不同。从表 1可知:1)HMM与SVM分类思想的不同带来了识别性能上的差异。一般而言,SVM是一种判决模型即分类器,而HMM是一种生成模型即统计模型。在分类对象是无序集的情况下,通常分类器的识别率优于生成模型。但对于探地雷达回波序列这类前后具有相关性的有序信号而言,侧重对序列变化过程建模的HMM更为有效。HMM将若干A-scan组成的序列作为一个整体,整体的各部分之间具有相关性,因此,序列这一整体降低了其中每个A-scan错分的可能性;而SVM仅限于对A-scan组成的无序集合分类,割裂了原序列A-scan之间的相互关系,即便采用多通道统计方法进行修正,其性能较HMM也略逊一筹。2)在隐含状态数N相同的情况下,GMM中的高斯分量个数越多,对模型的描述越精细,识别效果越好。

表1 SVM与HMM(隐状态数N=3)识别结果对比
在HMM的实际应用中,隐状态个数N与GMM中的高斯分量个数M的确定始终是讨论的热点问题。本文设隐状态个数N=3,物理意义明确,但其合理性也需实验验证。表2即验证了在GMM分量个数确定的情况下不同隐状态个数对HMM识别结果的影响。在方案Ⅰ中的不充分训练实验中,隐状态个数为3时识别效果最好,由此可以得出结论:当训练集所提供的信息并不充分时,隐状态个数为3的HMM具有最好的推广能力。在大多数实际情况下,训练集数据所提供的信息往往不可能充分,因此,前述假设在实际应用中具有合理性。当然,当训练集信息较为充分时,模型本身的精细程度会随着隐状态个数的增加而增加,其识别性能也相应提升。
还需指出,上述实验将2类土质、4类目标、3个不同深度的情况细化为17个类别,对此17类分别建立模型并进行识别,模型库细致且全面,涵盖了诸如对同一深度、同一土壤中的不同的目标进行识别等各种子问题。在实际应用中,可针对不同需要建立条件更为宽松的模型库。例如,可将上述实验中同一目标在不同深度、不同土质的数据所训练得到的模型合并为单一模型库,则此模型库在埋设深度与埋设土质方面更具普适性而对埋设目标更具专一性。
在本文所述算法中,隐马尔科夫模型的模型训练过程计算量最大但可离线完成,模型的在线识别并不影响实时运算速度。对于计算A-scan信号的时频联合分布图像及其纹理描述算子,可在前期加入适当的A-scan信号截断及时频图像主要区域分割以减少计算量。另外,所采用时频分析方法的抗噪能力很大程度上决定了本文算法的抗噪性能,可在实际应用中对时频分析方法加以选择。

表2 不同隐状态个数HMM的识别结果对比(观察序列概率中GMM分量个数M=1)
5.结 论
本文以A-scan为基本对象,提出采用EN、CP、SODM等六个纹理描述算子对时频分析得到的时频联合图像进行描述,直接反映A-scan信号的变化特征。在识别环节,考虑到实际扫描过程中天线与目标之间“由远及近再及远”的变化过程,采用连续HMM对不同目标的探测过程建模,实现了基于扫描过程的多目标识别。实验对比分析表明:这种基于过程的目标识别方法比对无序特征集合进行分类的SVM方法具有更好的效果。
[1] FURUTA K,ISHIKAWA J.Anti-personnel Landmine Detection for Humanitarian Demining[M].1st Edition.London:Springer-Verlag London Limited,2009.
[2] DANIELS D J.Ground Penetrating Radar[M].2nd Edition.London:Institution of Electrical Engineers,2004.
[3] 吴仁彪,刘家学,张 蓓.探地雷达地杂波抑制方法研究进展[J].信号处理,2005,21(4A):510-513.WU Renbiao,LIU Jiaxue,ZHANG Bei.Survey on GPR ground bounce removal[J].Signal Processing,2005,21(4A):510-513.(in Chinese)
[4] SAVELYEV G T,KEMPEN VAN L,Sahli H,et al.Investigation of time-frequency features for GPR landmine discrimination[J].IEEE Trans.Geoscience and Remote Sensing,2007,45(1):118-129.doi:10.1109/TGRS.2006.885077.
[5] WONG D C,NGUYEN L H,GAUNAURD G C,et al.Time-frequency analysis for radar classification of land-mineimages[J].Journal of Electronic Imaging,2007,16(3):033014.doi:10.1117/1.2776354.
[6] GUHA S,KRUSE S and WANG P.Joint time-frequency analysis of GPR data over layered sequences[J].The Leading Edge,2008,27(11):1454-1460.doi:10.1190/1.3011017
[7] 周辉林,田 茂,熊俊志.探地雷达回波信号的特征提取和分类[J].电波科学学报,2006,21(4):586-589.ZHOU Huilin,IAN Mao,IONG Junzhi.Feature extraction and classification of ground penetrating radar echo signals[J].Chinese Journal of Radio Science,2006,21(4):586-589.(in Chinese)
[8] 李建勋,郑军庭.超宽带探地雷达自动目标识别研究[J].电波科学学报,2005,20(4):535-540.LI Jianxun,ZHENG Junting.Automatic target recognition for ultra-wideband ground-penetrating radar[J].Chinese Journal of Radio Science,2005,20(4):535-540.(in Chinese)
[9] 胡进峰,周正欧.基于核方法的探地雷达目标特征提取方法[J].电波科学学报,2005,20(5):671-674.HU Jinfeng,ZHOU Zhengou.GPR target feature extraction based on kernel method[J].Chinese Journal of Radio Science,2005,20(5):671-674.(in Chinese)
[10] JOONKI P,CHEOLHA P L,MONGIA.Imageprocessing-based mine detection techniques:A review[J].Subsurface Sensing Technologies and Applications,2002,3(3):153-202.
[11] GADER P D,MYYSTKOWSKI M,ZHAO Y.Landmine detection with ground penetrating radar using hidden markov models[J].IEEE Trans.Geoscience and Remote Sensing,2001,39(6):1231-1244.
[12] FRIGUI H,HO K C,GADER PD.Rea-ltime landmine detection with ground penetrating radar using discriminative and adaptive hidden markov models[J].EURASIP Journal on Applied Signal Processing,2005,2005(12):1867-1885.doi:10.1155/ASP.2005.1867.
[13] ZHANG X P,GADER P D,HICHEM F.Feature learning for a hidden markov model approach to landmine detection[C]//Proc.SPIE,6553,2007,pp:655327.doi:10.1117/12.722593.
[14] FRIGUI H,MISSAOUI O,GADER PD.Landmine detection using discrete hidden markov models with gabor features[C]//Proc.SPIE,6553,2007,pp:65532A.doi:10.1117/12.722241.
[15] 王 群,何云龙,王春和,等.基于神经网络的探地雷达探雷研究[J].电波科学学报,2001,16(3):398-403.WANG Qun,HE Yunlong,WANG Chunhe,et al.Study of mine detection with GPR based on neural networks[J].Chinese Journal of Radio Science,2001,16(3):398-403.(in Chinese)
[16] ZHANG J,LIU Q,NATH B.Landmine featureextraction and classification of GPR data based on SVM method[C]//ISNN 2004,LNCS 3173,2004,636-641.doi:10.1007/978-3-540-28647-9¯ 104
[17] 胡进峰,周正欧,孔令讲.探地雷达多目标识别方法的研究[J].电子与信息学报,2006,28(1):26-30.HU Jinfeng,ZHOU Zhenou,KONG Lingjiang.Researches on GPR multi-object recognition[J].Journal of Electronics&Information Technology,2006,28(1):26-30.(in Chinese)
[18] HARALICK R M,SHANMUGAM K,DINSTEIN I.Textural features for image classification[J].IEEE Trans.Systems,Man and Cybernetics,1973,SMC-3(6):610-621
[19] HORNG M-H.Texture feature coding method for texture classification [J].Optical Engineering,2003,42(1):228-238.doi:10.1117/1.1527932.
[20] 王炳锡,屈 丹,彭 煊,等.实用语音识别基础[M].北京:国防工业出版社,2005:188-190.
[21] Royal Military Academy of Belgian.HUDEM Project,UWB GPRdata[DB/OL].Ispra:DG Joint Research Centre,1999-12-16[2010.7].http://apl-da-tabase.jrc.it/Home/Radar/Non-JRC/RMA¯ UWB¯GPR/.
