有限厚度平面周期结构的快速算法研究
2011-08-08车永星侯新宇
车永星 侯新宇
(电子薄膜与集成器件国家重点实验室,四川 成都610054)
1.引 言
平面周期结构,尤指频率选择表面(Frequency Selective Surface,FSS)是由无源谐振单元按一定的排列方式组成的准二维平面周期阵列[1]。它对某些频带内的入射电磁波呈全反射特性,而对另一些频带内的入射波则呈透射特性。其在微波毫米波领域的应用非常广泛,如滤波器设计、微带电路、天线散射等。
在传统的许多含有缝隙的FSS辐射结构分析时一般都假设金属屏的厚度为零,由于新的应用以及频率向更高发展的需要,必须将金属FSS屏的厚度考虑在内[2]。有许多全波法可以求解一般的孔径问题,但缺乏简便性和可用于零厚度孔径下直接积分公式模型(即2.5-D模型)的内部一致性。因此,研究可精确求解有限厚度金属屏,且同时具有与零厚度情况下相似的简便性的有效近似法是非常有必要的。
根据已有的关于求解周期结构问题的文献[3][4],可以看到基于矩量法求解的积分公式法(Integral Equation-Method of Moments,IE-MoM)是一种高精度的算法。但IE-MoM算法需要可靠准确的相关格林函数,而对于周期问题精确定义的格林函数会引出另一问题,即周期格林函数的慢收敛性。这就要求对现有的一般或特殊形式的加速技术作进一步的研究。
由文献[5][6]可知非线性级数加速法Shanks变换在通常情况下有较好的收敛,但在靠近源的区域会遇到困难。由文献[7]可知特殊加速算法Ewald变换则对自由空间格林函数有非常快的收敛。
论文综合采用了一般分析方法中Shanks变换和特殊分析方法中Ewald变换的优点,针对加速多层周期格林函数,尤其是矢量位格林函数,给出了一种新的有效的加速算法。此算法将屏的有限厚度并入零厚度情况下的算法或公式中,同时不增加计算时间和计算复杂度。最后,文中利用此方法对有限厚度的四腿加载单元FSS做了相应计算,给出了相应的计算结果。
2.有限厚度FSS分析
2.1 积分方程-矩量法(IE-MoM)
首先,对FSS做离散化处理。在FSS上定义一个周期单元,并将每个周期单元表面离散为多个网格,为了较好地近似实际表面,采用三角形或矩形组成的划分网格。任何由周期结构的散射或辐射所引出的问题均可以表达为如下积分方程

式中,算子L为积分-差分算子,其将未知的表面电流 a和已知的激励v联系在一起。在矩量法(MoM)中,将未知电流a展开为一组N维矢量基函数fi的线性组合,其表示如下

然后将积分方程(1)与矢量权函数组wi做内积,方程可离散化为
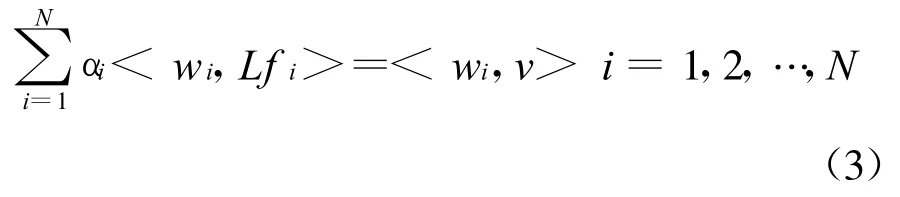
方程(3)也可以简单表达如下

式中 :Z=[zij]N×N是 MoM 矩阵 ;V=[vj]N×1为激励矢量;I=[ai]N×1表示未知电流系数。在这里权函数wi=f i.
由于电流和磁流结合不适于模拟周期结构,因此,在这里以位格林函数作为基函数和权函数。图1为单层介质衬底上的平面周期结构,其中介质衬底厚度为h,任意形状的相同单元分别沿x轴和y轴以周期a、b分布,平面波以角度 θin和 φin照射,在这里假设导体厚度可忽略不计。
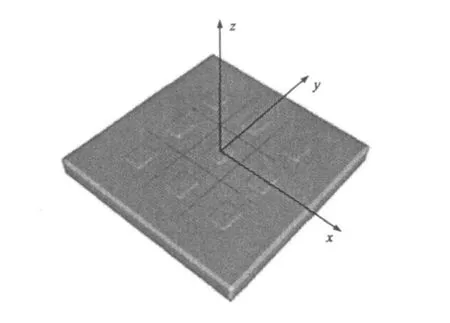
图1 单层介质衬底的平面FSS
如果假设表示无周期边界的二维自由空间或层介质中的格林函数为G0(x-x′,y-y′),则对于上述周期结构的格林函数的“空间域”公式表示如下
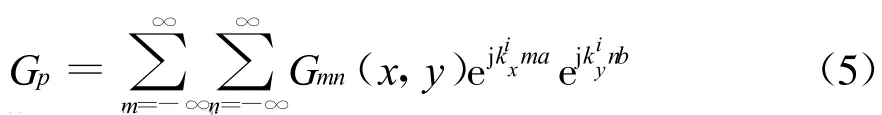
式中:Gmn(x,y)=G0(x-x′-ma,y-y′-nb)=ksinθicosφi和=ksinθisinφi分别为波传播矢量的x轴分量和y轴分量;m,n分别表示沿x轴方向的第m个单元,沿y轴方向的第n个单元。
应用二维泊松求和公式[7]及傅里叶变换,由公式(5)即可得到频域的周期格林函数如下
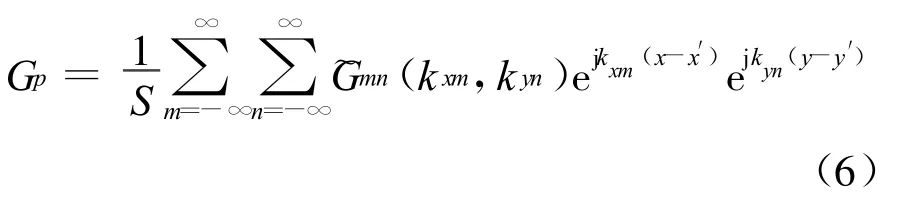
2.2 加速算法
在矩量法求解积分方程方法中,要求有可靠稳定的周期格林函数,但这同时会引出另一问题,即周期格林函数的慢收敛。为了保证计算时间在可接受范围内,并可以提供精确的计算结果,在计算中必须使用加速算法。一种针对加速多层周期矢量位格林函数的加速算法如下。首先将周期格林函数表达式(6)重新写为
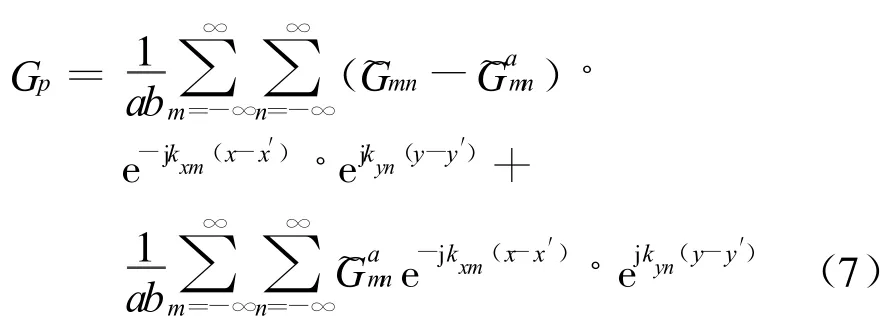
式中:矢量位周期格林函数由两部分组成,其中前一项为“动态”部分,后一项为“静态”部分。在模式和的“动态”部分的收敛中应用改进的Shanks变换
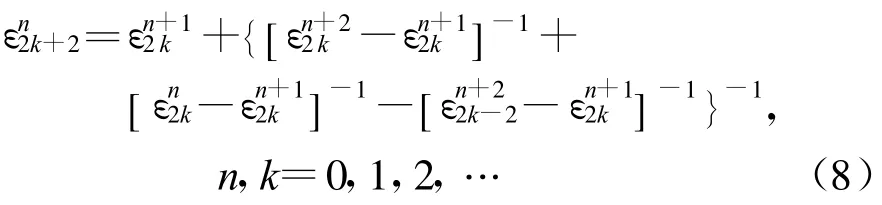
初始条件为
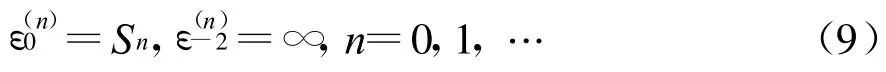
式中:Sn为级数的n项部分和,当n→∞时,Sn→S,S为级数和。利用上述级数收敛变换,模式和的“动态”部分将只需计算偶数阶部分,且有更好的数值稳定性和精度,得到快速收敛。在“静态”部分的收敛问题中应用Ewald变换可得

式中的补余误差函数将使得级数迅速收敛。将式(8)和式(10)合并后,即可实现对矢量位周期格林函数的加速收敛。
2.3 有限厚度FSS的算法实现
对于有限厚度的缝隙型FSS,可以分解为两部分分别求解,即内问题(缝隙内部区域)和外问题。外问题应用2.1节给出IE-MoM 方法求解,并利用2.2节给出的加速算法加速MoM 的计算速度。对于内问题,将缝隙腔体由具有相同几何截面的2-D目标代替[8-10],然后通过修改相应格林函数引入缝隙厚度,利用文献[11]给出的从有限厚度到零厚度位格林函数的平滑转换,即可在不增加额外复杂度的情况下对缝隙内部区域进行求解。
3.数值结果与分析
3.1 模 型
以图2所示的四腿加载单元FSS为例。其中单元周期D=7 mm,单元缝隙宽度w=0.2 mm,偶极子长度L=4.2 mm,偶极子宽度t=1.2 mm,FSS屏厚度为h,衬底材料相对介电常数εr=4.2,损耗正切 tanδ=0.02,衬底厚度h1=2 mm.
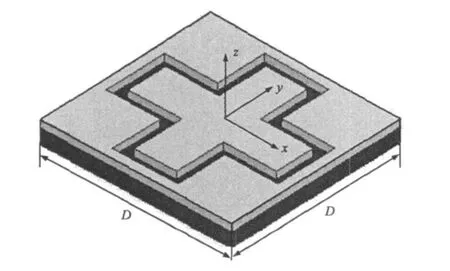
图2 FSS单元模型
3.2 传输系数
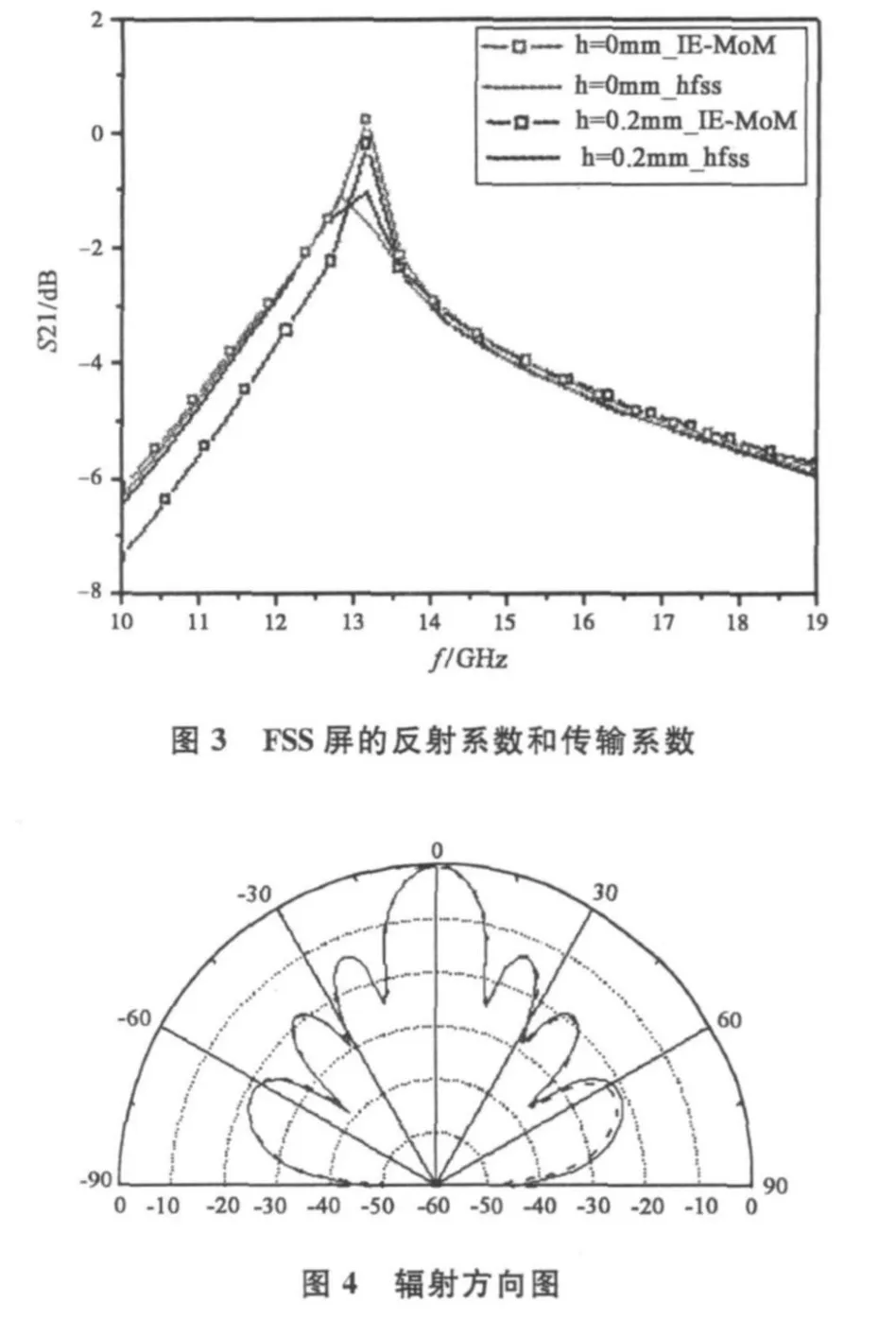
分别利用上述算法和全波电磁仿真软件HFSS对图2所给FSS单元的传输系数进行计算。假定平面波沿法向入射,在FSS屏厚度为h=0 mm,0.2 mm(大约为 λ/200,由文献[1]可知,当屏厚度大于λ/1000时不可忽略)时的传输曲线如图3所示。由图可知,由于厚度的存在FSS屏的谐振点略向高频偏移。通过对用文中所给方法和HFSS仿真结果的比较,两种方法取得了很好的一致性。
3.3 远场散射
为了检验厚度对远场参数的影响,对图2所示FSS结构的散射进行了计算。无限周期格林函数作为3×3单元阵列的一次近似,使用平面波源沿法向入射。格林函数的无限求和在前三个部分求和后截断。辐射方向图如图4所示。实际上,无限方法对于无限阵列中的单元能给出更好近似解,而在有限阵列中会受到边缘散射的影响。从图中可以明显地看出,本文方法与全波方法计算所得结果基本一致。
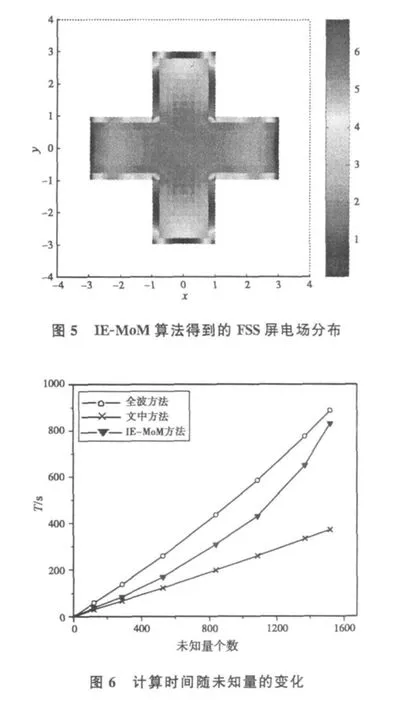
3.4 表面电场分布
图5给出了由IE-MoM算法结合矢量位周期格林函数加速算法计算得到的FSS单元电场二维分布图。屏厚度为h=0.2 mm,由电场方向沿y轴的平面波激励。在两个方向上,周期格林函数均只取前40项,计算速度得到明显提高。
3.5 计算时间
由全波方法、一般IE-MoM算法和结合了加速算法的IE-MoM算法所得计算时间随未知量的变化曲线如图6所示。平面波沿法向入射,电场沿y轴方向极化。由图可知,随着未知量个数的线性增长,全波算法和一般IE-MoM算法所耗时间的增长率逐渐增大,而加速计算的IE-MoM算法所耗时间只近似于线性增长,虽然计算时间没有得到大幅度的提高,但仍较另两种方法更简单快速。
4.结 论
将积分方程矩量法应用于有限厚度平面周期结构的电磁特性的求解计算,并综合采用了一般加速方法Shanks变换和特殊加速方法Ewald变换的优点,给出了针对矢量位周期格林函数加速的新的有效加速算法。通过对有限厚度屏的反射系数、传输系数、远场辐射、表面电场分布的计算,表明文中所述算法与全波电磁仿真软件 HFSS所得结果具有很好的一致性,同时,在计算时效上得到了显著提高。
[1] M UNK B.A.频率选择表面理论与设计[M].侯新宇,译.北京:科学出版社,2009.
[2] PARK H H,EOM H J.Electromagnetic scattering from multiple rectangular apertures in a thick conducting screen[J].IEEE Trans.Antennas Propagation,1999,47(6):1056-1060.
[3] ITOH T.Numerical Techniques for Microwave and Millimeter-wave Passive Structures[M〛.New York:Wiley,1989.
[4] 杨 卓,薛正辉,李伟明.平面波展开结合矩量法分析频率选择表面[J].电波科学学报,2009,24(2):314-317.YANG Zhuo,XUE Zhenghui,LI Weiming.Analyzing frequency selective surface with plane wave approach and the method of moments[J].Chinese Journal of Radio Science,2009,24(2):314-317.(in Chinese)
[5] BREZINSKI C,ZAGLIA M R.Extrapolation Methods-theory and Practice[M].Amsterdam:Elsevier Science Publishers,1991.
[6] KINAYMAN N,.AKSUN M I.Comparativestudy of acceleration techniques for integrals and series in electromagnetic problems[C]//Antennas and Propagation Society International Symposium,1995,2(2):1037-1040.
[7] PAPOULIS A.Systems and Transforms with Applications in Optics[M].Malabar,Florida:Kreiger,1981.
[8] JORDAN K,RICHTER G,SHENG P.An efficient numerical evaluation of the Green's function for the Helmholtz operator on periodic structures[J].Journal of Computational Physics,1986,63:222-235.
[9] STEVANOVI C I,CRESPO-VALERO P,MOSIG J R.An integral equation technique for solving thick irises in rectangular waveguides[J].IEEE Trans.Microwave Theory Tech.,2006,54(1):189-197.
[10] STEVANOVI C I,MOSIG J R.Efficient electromagnetic analysis of line-fed aperture antennas thick conducting screens[J].IEEE Trans.Antennas Propagation,2004,52(11):2896-2903.
[11] MOSIG J R.Scattering by arbitrarily-shaped slots on thick metallic screens:An approximate solution[J].IEEE Trans.Antennas Propagation,2004,52(8):2109-2117.
