粒子群阵列天线方向图适应值函数研究
2011-08-08冯全源
刘 东 冯全源
(1.西南交通大学电气工程学院,四川 成都 610031;2.西南交通大学信息科学与技术学院,四川 成都 610031)
1.引 言
近年来,粒子群优化(PSO)算法[1]得到了广泛的关注。PSO算法是KENNEDY与EBERHART提出的一种模仿鸟群社会行为的智能优化算法,已成功地应用于许多工程优化问题中[2]。
阵列天线方向图综合实质上是多目标优化问题,具有多参数、非线性、不可微甚至不连续等特性。这类大规模非线性的全局优化问题,传统的最小二乘等局部搜索方法很难满足要求[3]。智能优化算法在解决全局优化问题时表现出良好的性能,将智能优化算法与阵列天线方向图综合相结合是一个研究热点[4-11]。
文献[4]将遗传算法用于阵列天线方向图综合,文献[5]将粒子群算法用于阵列天线方向图综合,文献[6]在LDW-PSO算法基础上改进了ω变化策略同时对全局最优粒子进行扰动,并将改进算法应用于阵列天线方向图综合,文献[7]将遗传算法中的交叉变异思想引入PSO算法并应用于阵列天线方向图综合,文献[8]在LDW-PSO算法的 ω变化策略上加入了停滞策略,将算法应用于阵列天线方向图综合,文献[9]研究了阵列天线适应值函数的选取,给出了一个较为通用的适应值函数表达式,并用阵列天线方向图综合进行了验证。这些算法在旁瓣抑制和深零陷生成上取得了良好的效果,其改进思路是通过改进优化算法来提升阵列天线方向图综合效率,算法越来越复杂且算法通用性也很难兼顾。
采用智能算法对阵列天线方向图综合进行优化(本文此处及以下简称方向图优化)一方面取决于算法的效率,一方面取决于适应值函数的选取。由遗传算法,粒子群算法等群体智能算法的工作原理可以知道,适应值函数返回值对种群朝着全局最优点迁移起着至关重要的作用。如果适应值函数指示性不好,区分度不强,那么算法性能再好也很难收敛。改进适应值函数可以更好地将优化问题与已有算法相匹配,充分发挥算法的优化能力。
本文提出了一种分阶段适应值函数,其基本思想是当将多目标优化问题分解成多个阶段目标,不同阶段的指标和侧重点都有不同。仿真结果表明在多零点约束低旁瓣方向图优化应用中,不改变PSO算法的情况下,采用分阶段适应值函数可以大幅提升算法性能。
2.方向图优化中的适应值函数
阵列天线方向图综合是通过对阵元位置,激励幅值及相位进行调整来实现预设的阵列天线波束形状。最常见的阵列天线是等距直线阵列天线,其方向图优化是通过调整N个各向同性辐射单元的激励电流幅度和相位,从而使天线的远场方向图达到预期的特性指标要求。
采用智能算法来实现等距直线阵列天线方向图优化就是根据不同参数组对应的适应值函数大小来决定各个阵元电流幅值相位的调整大小和方向。如果适应值函数小于设定的数值,表示当前参数能够满足当前设计指标。
方向图优化常用的适应值函数有两种[9]。一种是基于不同角度值上的误差均方和,如式(1)
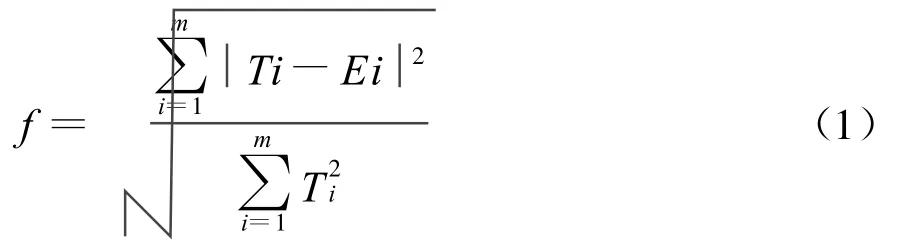
式中:m为整个方向图角度范围上的采样点数;Ti为在第i个采样点上的设计;Ei为第i点上的计算值。
另一种是基于方向图性能指标加权和,如式(2)所示
式中:θ0和θm为设计主瓣位置和计算主瓣位置;SLLmax为最高旁瓣电平;θBWFN为第一零陷主瓣宽度;w1至w3为不同指标的加权值。式(2)中只包含主瓣位置,主瓣宽度以及最高旁瓣电平。文献[9]中式(3)包含更多方向图指标。不过适应值函数包含指标越多,优化起来也就越困难。对于多目标优化问题来说,不同指标加权值如何平衡目前还没有一个可以遵循公式,对于复杂指标的多目标优化问题更是如此。
3.算法效率与适应值函数策略
对于遗传算法,粒子群算法等基于种群的智能优化算法来说,其寻优本质是基于适应值函数反馈的概率寻优,都存在早熟收敛的问题。
3.1 适应值函数与算法收敛效率
文献[10]指出在停滞状态下,如果特征值小于1,PSO算法中的粒子种群会集中到一个平衡点附件。实际上,在PSO算法中,如果参数设置在收敛范围内,除全局最优粒子外的粒子都向全局最优粒子靠拢,并聚集在全局最优粒子附近的区域。对于不太复杂的优化问题,全局最优极值点在全局最佳粒子附近的概率较大,粒子群算法这种聚集特性会有利于算法收敛。但是当维数增高或优化指标较多时,这一策略也会使整个粒子群很快聚集到局部极值点附近,保持聚集状态而非扩大搜索区域,从而导致算法早熟收敛。为了防止早熟收敛,改善收敛效率,国内外学者都对算法做了大量改进[2],不过都没有从本质上改进算法防止早熟收敛的方法,也没有针对所有优化问题通用的改善方法。
优化算法早熟收敛一方面是由于算法的固有特征造成的。另一方面,适应值函数的指示性,区分性也和算法寻优效率关系密切。对于复杂多目标优化问题来说,合适的适应值函数能够让算法区分局部极值点和全局最优点,同时也能区分主要指标和次要指标。文献[9]中通过不同的加权值来区分方向图优化中的主要指标和次要指标,但在方向图优化中,在优化进行不同的阶段,不同的指标改进不是同步的,往往次要指标的改进会导致参数寻优区域偏离主要指标改进的方向。由于多指标加权方式的适应值函数存在“顾此失彼”以及次要指标“喧宾夺主”等问题,所以单纯依靠一个通用的适应值函数来解决不同类型的方向图优化在实际实现中比较困难。
3.2 分段适应值函数策略
采用通用统一的方向图优化适应值函数进行方向图优化必须选取合适加权值,不然会导致算法优化效率降低,尤其是在复杂多目标方向图优化应用中,算法很难收敛。
阵列天线远场方向图在某个固定角度的特性和所有阵元的电流幅值相位均相关,任何一个阵元电流幅值阵元发生改变,整个方向图特性都会改变。实际的方向图往往具有多个设计指标,对主瓣位置和宽度,零陷位置和深度,还有最高旁瓣电平都有一定要求。同时优化这些指标往往是矛盾的,满足零陷位置和深度的参数,其最高旁瓣电平很难降低;要顾及主瓣宽度,零点位置和深度又无法保证这使得采用智能算法来进行方向图优化特别是复杂多指标方向图优化比较困难。
由于实现智能算法性能的大幅改进比较困难,本文从适应值函数的角度出发,通过选用与具体优化问题更加匹配的分段适应值函数来提高阵列天线方向图优化的效率。这样可以在不改变原来算法的情况下,充分发挥算法优化潜力,提升整体优化效果。本文采用分阶段提高适应值函数指标的方法来完成复杂多指标方向图优化,取得了良好的效果。
3.3 适应值函数分段方法
适应值函数分段可以通过试验方法确定,需要选择一个合适的试验次数以及优化指标分段值。智能算法本质上是随机优化算法,其优化成功概率随着优化问题复杂性的增加而降低。在优化复杂问题时,较大的试验次数可以取得更好的优化结果,通常试验次数不少于20。优化指标分段根据试验成功率来确定。前一个阶段的试验成功率越高,多样性越好,但导向性越差;反之多样性降低,导向性提高。前一阶段优化指标过高过低都会降低后一个阶段的优化成功概率。如果适应值分为两个阶段,那么可以用不低于10%的优化成功率来选择第一个阶段的优化指标。
4.仿真实例
本文选取N个各向同性辐射单元组成的等间距直线阵列天线进行综合,各个阵元的相位相同,只调整阵元的激励电流的幅度来使得天线的远场方向图达到预期的特性指标要求。等间距的直线阵天线的远场方向图为

式中:φ是波束与线阵法线间的夹角;N为阵元个数;In为各个阵元的激励电流幅值;φn为各阵元激励电流的相位;d是阵元间距;k=2π/λ,λ是波长。不考虑阵元间耦合。
为了比较不同适应值函数策略的效果,本文中所有仿真实例都采用文献[8]中的LDW-PSO算法,w范围为[0.1,0.9]。
4.1 实例1
考虑文献[8]中的实例2,均匀直线阵,N=20,阵元间距d为λ/2,激励电流相位均为0(边射阵),电流幅值对称,只优化电流幅值。要求旁瓣电平小于 -15 d B,零陷位置[-20°、-25°、-30°、-35°、-40°、-45°、-50°],零陷深度小于 -85 dB.由于设计指标很高,文献[8]中提及的所有算法都不能全部收敛,标准LDW-PSO算法采用200个粒子,400次迭代,20次试验中甚至没有一次收敛到0。
本实例的设计指标只考虑最高旁瓣电平以及指定位置零陷电平,适应度函数的选取在文献[8]中的目标函数
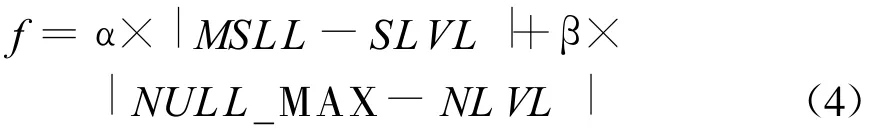
式中:MSLL为最高旁瓣电平;SLVL为设计最高旁瓣电平;NULL¯MAX为所有指定角度处零陷电平的最大值;NLVL为设计零陷电平值。取α=0.8,β=0.2。
本实例采用两段适应值函数策略,第一阶段适应值函数中的收敛指标为指定位置零陷深度不高于-75 dB,旁瓣电平小于-5 dB.第二阶段适应值函数收敛指标为指定位置零陷深度不高于-85 dB,旁瓣电平小于-15 dB.优化算法使用标准LDW-PSO算法,粒子个数200,迭代次数200,每阶段试验次数均为20。
第一阶段20次试验2次收敛,第二阶段将收敛的2个参数作为初始值,各做10次试验,一共有2组收敛。图1为优化得到的方向图,表1为各阵元电流幅值。
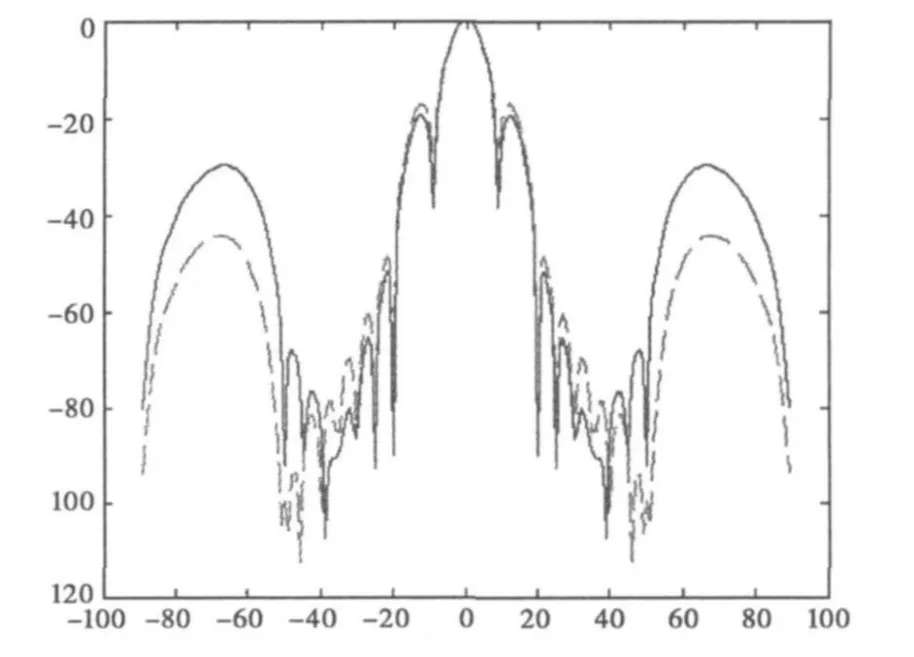
图1 实例1方向图

表1 实例1各阵元电流幅值
4.2 实例2
均匀直线阵,N=40,阵元间距d为 λ/2,激励电流相位均为0(边射阵),电流幅值对称,只优化电流幅值。要求旁瓣电平不低于-43 d B,主瓣宽度不大于12°。
这是一个超低旁瓣方向图优化,设计指标也比较高,比文献[11]的旁瓣电平低0.5 dB,主瓣宽度也更窄。采用标准LDW-PSO算法,使用式(5)作为适应值函数,200个粒子,迭代次数400,20次试验无收敛。
本实例的适应度函数为:

式中:MSLL为最高旁瓣电平;SLVL为设计最高旁瓣电平;BodeWidth主瓣宽度。取α=0.8,β=0.2。采用两阶段适应值策略,第一阶段的设计指标为方向图旁瓣电平不低于-40dB,主瓣宽度小于20°。第二阶段设计指标为方向图旁瓣电平不低于-43 d B,主瓣宽度不大于12°。采用200个粒子,200次迭代,20次试验。第一阶段12次收敛,第二阶段对第一阶段优化结果继续优化200代,6组收敛。图2为优化后的方向图,表2为阵元电流幅值。
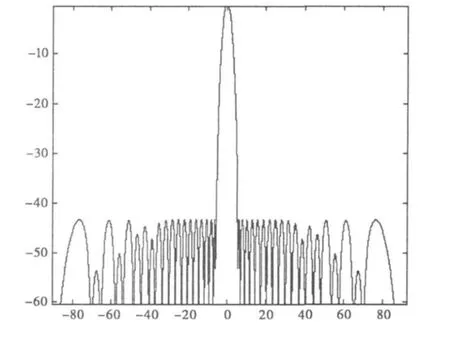
图2

表2 实例2各阵元电流幅值
实例1和实例2均为多目标复杂方向图优化,在目前公开文献中未见同等条件下有更高的设计指标。从图1中可以看出:分两阶段优化得到的2组方向图均能在指定位置满足零陷深度要求,在有些位置甚至低于-110 dB,同时旁瓣电平也都低于-15 dB.图2中旁瓣电平低于-43 dB,第一零点主瓣宽度11.2°,达到了设计指标。
5.讨 论
方向图优化是一个多目标优化问题,存在具有多参数、非线性、不可微甚至不连续等特性。由于阵元数量和解空间维数一致,当阵元数较多时,不满足收敛条件的极值区域远远多于满足收敛条件的极值区域,基于搜索的智能算法如遗传算法(GA),PSO等容易陷于局部极值导致早熟收敛。
在多目标复杂方向图的优化中,由于各个优化指标之间的加权值很难调整到合适的比例,整个种群在解空间搜索时,很容易沿着某个优化目标改进较快的方向前行,通常是权重较大或者约束较为简单的目标,从而导致局部收敛。
在使用PSO及其改进算法优化多目标复杂指标的方向图时,现有防止早熟收敛的策略如最优值扰动,保留全局最优粒子的重新初始化等均无法保证算法能够跳出局部极值,实际效果非常有限。全局最优粒子扰动相当于单个粒子小范围的随机搜索,只有在算法开始阶段可以改善整个粒子群向最优粒子聚集的路径,在早熟收敛时基本起不到效果。重新初始化策略可以让整个粒子群重新由整个空间分布再次向全局最优值位置进行搜索,由于PSO算法聚集特性,整个种群会在很短的时间内聚集到全局最优粒子附近,在这个期间,粒子搜索到比全局最优粒子更好位置的概率非常小,甚至不如重新搜索。
本文采用的分阶段适应值函数策略,由于各个指标分阶段提高,使得各个阶段更容易平衡各个优化目标,不会导致某个优化目标已经满足收敛条件而另外的优化目标还差距很远。这样在解空间中,局部极值区域的深度更浅,有利于种群跳出局部极值点,实现全局收敛。在实际方向图优化中,可以分两次或者更多阶段将方向图指标逐步提高至设计指标。
6.结 论
为了解决多目标复杂方向图优化很难收敛的问题,本文提出了一种分阶段适应值策略,可以在PSO算法性能不变的情况下提高优化效率。本文将此策略用于对阵列天线多零点低旁瓣方向图以及超低旁瓣和窄主瓣方向图的综合,取得了良好的效果,体现了该策略的有效性。
致谢 本文受到2009西南交通大学青年百人计划—中央高校基本科研业务费专项资金资助(项目编号:SWJTU09BR068)以及西南交通大学青年教师科研起步项目(2009Q014)资助。
[1] KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proc.of IEEE Interna-tional Conference on Neural Networks.IEEE Service Center,1995:1942-1948.
[2] del VALLE Y,VENAYAGAMOORTHY G K,MOHAGHEGHI S,et al.Particle swarm optimization:basic concepts,variants and applications in power systems[J].IEEE Trans.Evol.Comput.,2008,12(2):171-195.
[3] DENNIS J E Jr.Nonlinear Least Squares:State of the Art in Numerical Analysis[M].D.Jacobs Academic Press:1977 :269-312.
[4] 马云辉.阵列天线的遗传算法综合[J].电波科学学报,2001,16(2):172-176.MA Yunhui.Synthesis of the array antennas using genetic algorithm[J].Chinese Journal of Radio Science,2001,16(2):172-176.(in Chinese)
[5] 焦永昌,杨 科,陈胜兵,等.粒子群优化算法用于阵列天线方向图综合设计[J].电波科学学报,2006,21(1):16-25.JIAO Yongchang,YANG Ke,CHEN Shengbing,et al.Application of particle swarm optimization in antenna array pattern synt-hesis[J].Chinese Journal of Radio Science,2006,21(1):16-25.(in Chinese)
[6] 金荣洪,袁智皓,耿军平,等.基于改进粒子群算法的天线方向图综合技术[J].电波科学学报,2006,21(6):873-878.JIN Ronghong,YUAN Zhihao,GEN Junping,et al.The pattern synthesis of antennas based on a modified PSO algorithm[J].Chinese Journal of Radio Science,2006,21(6):873-878.(in Chinese)
[7] 高 波,金荣洪,耿军平.基于一种新的粒子群算法的天线方向图综合技术[J].电子与信息学报,2007,29(12):3015-3019.GAO Bo,JIN Ronghong,GEN Junping.Pattern synthesis of antenna array using a novel quasi pso algorithm[J].Journal of Electronics&Information Technology,2007,29(12):3015-3019.(in Chinese)
[8] 刘 东,冯全源.基于停滞检测粒子群算法的阵列天线方向图综合[J].电波科学学报,2009.LIU Dong,FENG Quanyuan.Pattern synthesis of antennas based on a modified PSO algorithm with stagnation detection[J].Chinese Journal of Radio Science,2001,16(2):172-176.(in Chinese)
[9] 范 瑜,金荣洪,刘 波,等.阵列天线方向图综合中的遗传算法目标函数研究[J].电子与信息学报,2005,27(5):801-804.FAN Yu,JIN Ronghong,LIU Bo,et al.Study on the objective function for the array pattern synthesis based on genetic algorithm[J].Journal of Electronics&Information Technology,2005,27(5):801-804.(in Chinese)
[10] CLERCM,KENNEDY J.Theparticle swarm explosion,stability,and convergencein a multidimensional complex space[J].IEEE Trans.Evol.Comput.,2002,6(1):.58-73.
[11] 李东风,龚中麟.遗传算法应用于超低副瓣线阵天线方向图综合[J].电子学报,2003,31(1):82-84.LI Dongfeng,GONG Zhonglin.Application of genetic algorithms in the pattern synthesis of ultra-low sidelobe linear array antenna[J].Acta Electronica Sinica,2003,31(1):82-84.(in Chinese)
