铁路集装箱空箱调运问题的遗传算法*

段 刚，张 慧，陈 莉，李引珍，刘永莉，陈志忠

(1.兰州交通大学交通运输学院，甘肃 兰州 730070;2.兰州铁路局货运处，甘肃 兰州 730070;3.兰州城市学院数学学院，甘肃 兰州 730070)

由于我国地区经济发展不平衡、各区域货物流量不均衡以及集装箱办理站之间集装箱到发量的不平衡，导致铁路适箱货源和箱源分布也不平衡。即使在同一地区，也会因季节和时间的变化而出现某一段时间集装箱空箱积压，另一段时间短缺的现象，从而导致空箱调运。频繁地进行空箱调运不但浪费铁路运能，而且空箱在运输途中支出的各种费用也给铁路运输企业增加了负担。集装箱的日常管理费用通常可以分为:空箱调运费、堆存费、修理费、集装箱租赁费、吊装费和其他费用，而集装箱空箱调运费用占总费用的1/4。因此，优化空箱调运方案并设计出高效的算法，对于减少空箱调运成本，提高铁路运能和集装箱使用效率，具有十分现实的意义。

1 研究现状

铁路空箱调运与空车调配问题无论从模型构造上还是求解方法上都非常相似，因此可以借鉴。熊红云等［1］和张得志等［2］采用矩阵表示染色体的遗传算法分别求解铁路空车和空箱调运问题，他们设计的交叉算子均对2个染色体的均值运算和取余运算的结果进行代数和计算，从而得到新的染色体，变异算子也都是对染色体子矩阵中的元素进行调整，区别是一个采用整数编码，一个采用十进制编码。果鹏文等［3］采用振荡法解决大规模路网上的空车调配问题，在事先不知道某个区段空车排空方向的前提下，预先人为指定该区段的空车排空方向，作为初始方案，使得区段上中间站的空车流，能够按照一定的原则归并到前方技术站;然后对初始方案进行计算，对区段空车方向不断进行调整，反复计算，直到指定的空车方向与计算结果相符合时为止。雷中林等［4］针对运输需求等不确定性建立了空车调配的随机机会约束模型，并设计了遗传算法求解。林柏梁等［5］设计了分步优化迭代算法求解线路能力约束下的铁路空车调配问题。还有应用神经网络法［6］、物体重心法［7］和区段中心优化法［8］求解问题。在此，作者从铁路运输实际出发，针对空箱调运模型，设计了一种新的遗传算法，可以高效求解空箱调运问题。

2 空箱调运问题的数学模型

2.1 参数与变量

S为空箱供应站集合，S={1，2，…，m};D为空箱需求站集合，D={1，2，…，n};ai为 i站可供应的空箱数，ai∈Z+，i∈S;bj为 j站需求的空箱数，bj∈Z+，j∈D;dij为 i站与 j站间的距离，i∈S，j∈D;xij为i站向j站调运的空箱数，决策变量。

2.2 空箱调运模型

空箱调运模型如下:

(1)式为目标函数，表示空箱调运的总距离最小;(2)式与(3)式为空箱供应与需求的平衡约束;(4)式为变量的非负和整数约束。

3 空箱调运问题的遗传算法

自从1975年Holland提出遗传算法后，因为其简单、鲁棒性好和并行计算等特点，从而在工程技术、自动控制、图像处理、人工智能和管理科学等众多领域得到了广泛应用。本文提出一种新的遗传算法，通过交叉与变异操作，在保证解的可行性基础上，能够快速高效求解空箱调运问题。

3.1 染色体的构成及种群的初始化

采用整数编码，以矩阵V表示一个染色体，

其中，xij∈Z+∪{0}，i∈S，j∈D 。显然，基因 xij表示i站向j站调运的空箱量，这样，染色体的基因型与其表现型完全一致，无需解码，因此以下对染色体和解不加区分。但要使得染色体可行，必须满足供需平衡的条件。以下种群的初始化，交叉算子和变异算子的操作，均围绕染色体的可行性来进行。

初始种群的产生采用下面的算法［1－2］:

步骤1 随机产生下标 i和 j，其中i∈ S，j∈D;

步骤2 计算 xij，xij=min{ai，bj};

步骤3 更新 ai和 bj，ai= ai－ xij，bj= bjxij;

步骤4 重复步骤1—步骤3，直到所有ai和bj都为0。

由上述算法产生的染色体必然对应一组可行解，其分配思想就是随机化的西北角法。

3.2 交叉算子

按交叉概率pc随机选择染色体V1和V2作为父个体，其中。为了使得交叉操作不破坏染色体的可行性，采用下面的方法产生子代染色体V3=(yij)和V4=(zij)。首先，令

其中，i∈ S，j∈ D，i和 j不同时为1，0 ＜ α ≤0.5。当i=1，j≥2时，(9)式和(11)式的最小值皆取第1项，而当j=1，i≥2时，两式的最小值皆取第2项。α为交叉参数，是本遗传算法中最重要的参数。实际上，文献［1］和［2］中的交叉方法可以看作是本交叉算子的特例，即α取值为0.5，也就是对2个父代染色体的对应基因求均值。而本文中，α取值更广泛，这样就能够扩大种群的多样性。

(9)式和(11)式可以保证子代染色体每行的调运量之和不会超过供应量，每列的调运量之和不会超过需求量，(10)式和(12)式能够保证调运量都非负，但却不能保证等式成立，故需要对调运量进行调整以满足平衡条件。

更新 yi1，j1，令 yi1，j1= φ +yi1，j1;遍历 i，j，直至所有行列都满足平衡。

3.3 变异算子

求解运输问题的表上作业法，其对基变量的调整采用闭合回路法。该方法虽然能保证解的可行性，但寻找闭合回路却相当耗时。本文借鉴该思想，采用基于矩形闭合回路的方法设计变异算子，可以大大减少计算量。

按变异概率pm选择染色体V5=(wij)，随机选择 i0，j0，i1，j1，其中 i0∈S，j0∈D，i1∈S/{i0}，j1∈ D/{j0}。当 wi0，j0wi1，j1＞ 0 ，即 wi0，j0和 wi1，j1同时为正数，取δ=min{wi0j0，wi1j1}。然后在矩形闭合回路 wi0j0，wi0j1，wi1j1，wi1j0中进行调整，令

其余基因wij取值不变，组成新的染色体V6。

3.4 评价函数和选择操作

由于染色体的可行性以及目标函数为线性函数，所以取目标函数为评价函数，即:

其中，V=(xij)。

采用基于轮盘赌的选择策略，详见文献［9］。

3.5 算法步骤

步骤1 初始化种群;

步骤2 通过交叉操作和变异操作产生子代染色体;

步骤3 计算每个染色体的评价函数，并记录最优染色体;

步骤4 通过轮盘赌选择染色体;

步骤5 重复步骤2—步骤4，直到满足停止条件。

其中，停止条件为可以定义为进化的最大代数，也可以通过比较前后两代最优染色体的变化情况确定停止条件，本文采用前者。

4 实验仿真

以兰州铁路局为例，对该局内集装箱办理站间的空箱调运进行优化。图1所示为兰州局的18个集装箱办理站。这里取2009年某月的集装箱运输数据，用以验证算法的有效性。各个集装箱办理站的空箱需求量、供应量以及两站之间的距离如表1所示，其中，距离为两站之间的最短路径长度。由于绿化、中堡、张家祠和鸳鸯镇4个集装箱办理站到发集装箱数量平衡，故没有出现在表1中。因为总需求量为554箱，而总供应量只有344箱，所以增加虚设供应站S6，其供应量为210箱。

图1 兰州铁路局集装箱办理站示意图Fig.1 Lanzhou Railway Bureau container handling stations

为了寻求交叉概率、变异概率以及交叉参数α的最佳取值，利用 VC6.0编程，在 Core 2 Duo＆2.2GHz、1G DDR2的惠普笔记本上运行通过，在每组概率组合下都做了10次测试，其中群体规模为20，遗传代数为600。首先令 α =0.1，Pm=0.1，交叉概率Pc在(0，1)区间每次变化0.05，评价函数的平均值和标准差的变化见图2和图3。显然 Pc的最优取值为0.65，在此基础上，变异概率Pm在(0，1)内每次变化0.05，同样可以得到评价函数的均值和标准差变化情况，见图4和图5。从图中可以看出，当Pm大于0.65时，评价函数的均值几乎相同，其标准差也比较接近，且都比较小，因此，选取 Pm=0.65。

表1 集装箱办理站间距离及供需表Table 1 The distance between container handling stations and supply and demand quantity

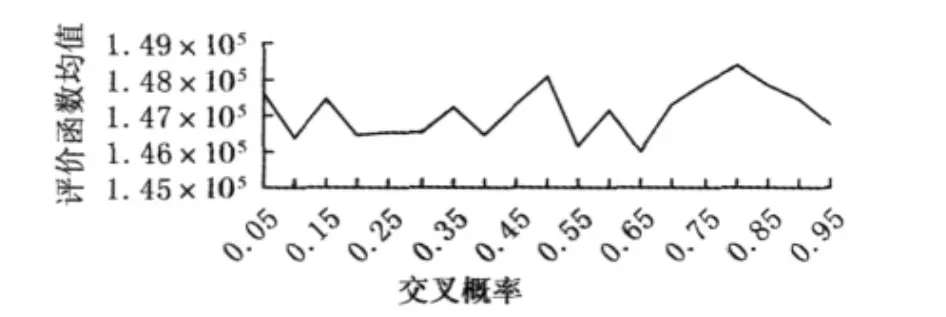
图2 不同交叉概率下评价函数平均值Fig.2 The average value of evaluation function under different crossover probability

图3 不同交叉概率下评价函数标准差Fig.3 The standard deviation value of evaluation function under different crossover probability

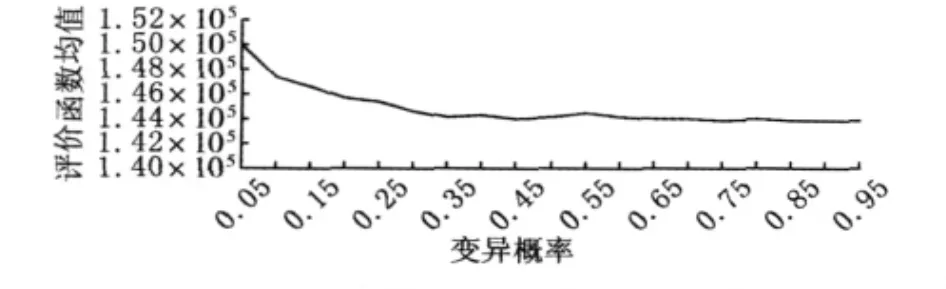
图4 不同变异概率下评价函数平均值Fig.4 The average value of evaluation function under different mutation probability

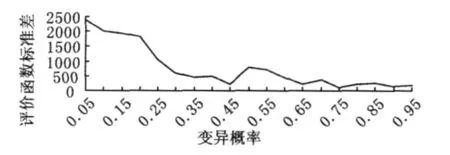
图5 不同变异概率下评价函数标准差Fig.5 The standard deviation value of evaluation function under different mutation probability

在最优交叉概率和变异概率组合下，令α在区间［0.05，0.5］内每次变化0.05，得到评价函数的均值和标准差，如图6和图7所示。当α取值为0.1，0.35和0.5时，评价函数平均值都比较小，标准差也相差不多，所以可以任选一个，本文取α=0.1。

图6 不同交叉参数值下评价函数均值Fig.6 The average value of evaluation function under different crossover parameter

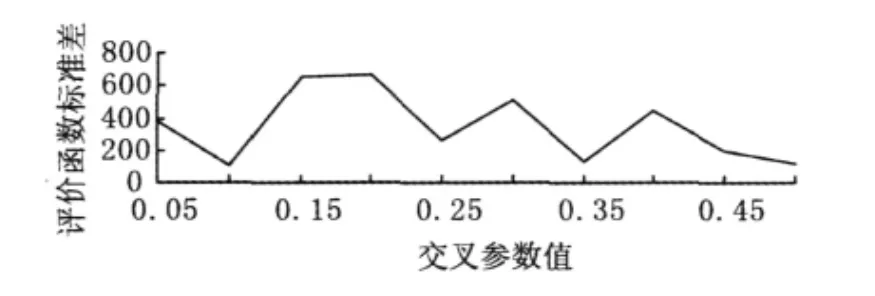
图7 不同交叉参数值下评价函数标准差Fig.7 The standard deviation value of evaluation function under different crossover probability

在以上各参数最优取值下，通过本文设计的遗传算法，当计算到520代时达到最优，评价函数为143689，收敛过程如图8所示(其中，从390代到510代，评价函数都为143720，与最优评价函数只相差31，图中显示不明显)。采用LINGO 9.0软件计算得到的最优解如表2所示，计算时间不到1 s(LINGO 9.0最小计时单位为s)。本遗传算法的计算时间仅为0.14 s，不但能得到上述最优解，而且还能得到另外一组最优解，如表3所示。不难看出，在表2中由金昌，兰州北，嘉峪关和白银市组成的闭合回路里，对调运量进行了1个单位的调整，即得到表3，而这正是本文中的变异操作。所以使用该遗传算法，不仅能在不同的计算中得到这2组最优解，还能在一次计算中同时得到这2组最优解，而这是LINGO软件做不到的。

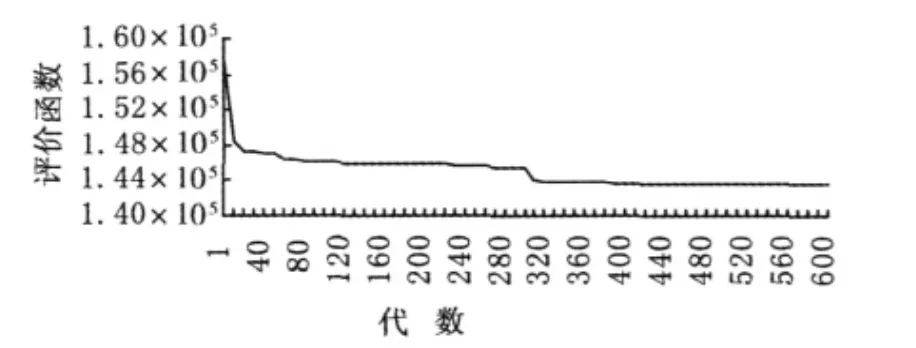
图8 遗传算法收敛图Fig.8 Genetic algorithm convergence figure

表2 应用LINGO计算得到的最优调运量Table 2 The best solution solved by LINGO software container

表3 另外一组最优调运量Table 3 The other best solution solved by genetic algorithm container

5 结论

铁路集装箱空箱调运优化模型与空车调运模型完全相同，因此，设计高效的算法就成为解决这类问题的关键。本文提出的遗传算法，交叉操作是对父代染色体进行线性组合并取整后经过适当调整得到子代染色体，变异操作则采用矩形闭合回路法。通过对兰州铁路局集装箱办理站的实例计算，表明该算法不但效率非常高，而且还能得到不同的最优解。关于交叉参数α的取值问题，本文采用固定值，通过测试找到其最佳取值。如果在计算过程中，对α进行调整，采用变参数法，或者直接对其进行编码并参与交叉和变异操作进行自适应调整，这样会进一步提高该算法的效率，以利于求解更大规模的问题，这将是我们下一步要研究的内容。

［1］熊红云，鲁五一，温红艳.铁路空车调配问题的遗传启发算法［J］.中国铁道科学，2002，23(4):118－121.XIONG Hong-yun，LU Wu-yi，WEN Hong-yan.Hereditary heuristic algorithm for empty car distribution in railway transportation［J］.China Railway Science，2002，23(4):118－121.

［2］张得志，谢如鹤，黄孝章.铁路集装箱空箱调度模型及求解算法［J］.中国铁道科学，2003，24(3):125－129.ZHANG De-zhi，XIE Ru-he，HUANG Xiao-zhang.Dispatch model and solution algorithm of railway empty container［J］.China Railway Science，2003，24(3):125 －129.

［3］果鹏文，褚 江，林柏梁.用振荡法解大规模路网上的空车调配问题［J］.中国铁道科学，2002，23(4):111－117.GUO Peng-wen，CHU Jiang，LIN Bo-liang.Reiterative adjusting method of empty wagon on large－scale railway network［J］.China Railway Science，2002，23(4):111－117.

［4］雷中林，何世伟，宋 瑞，等.铁路空车调配问题的随机机会约束模型及遗传算法［J］.铁道学报，2005，27(5):1－5.LEI Zhong-lin，HE Shi-wei，SONG Rui，et al.Stochastic chance－constrained model and genetic algorithm for empty car distribution in railway transportation［J］.Journal ofthe China Railway Society，2005，27(5):1－5.

［5］林柏梁，乔国会.基于线路能力约束下的铁路空车调配迭代算法［J］.中国铁道科学，2008，29(1):93－96.LIN Bo-liang，QIAO Guo-hui.Iterative algorithm of railway network empty cars distribution based on restriction of route capacity［J］.China Railway Science，2008，29(1):93－96.

［6］党建武.神经网络在铁路空车调度问题中的应用［J］.兰州铁道学院学报，1999，18(1):77－85.DANG Jian-wu.Application of neural networks to empty carriage scheduling in railway transportation［J］.Journal of Lanzhou Railway Institute，1999，18(1):77－85.

［7］纪嘉伦，林柏梁，李福志，等.用重心优化方法求解铁路网上空车调配问题［J］.铁道学报，2001，23(3):109－113.JI Jia-lun，LIN Bo-linag，LI Fu-zhi，et al.Distribution of empty wagons on railway network by using the center－of－gravity－ optimization method［J］.Journal of the China Railway Society，2001，23(3):109－113.

［8］果鹏文，林柏梁，余 洋.大规模路网上空车调配的区段中心优化法［J］.中国铁道科学，2001，22(2):122－128.GUO Peng-wen，LIN Bo-liang，YU Yang.The section center optimization method of empty car adjustment on large － scale railway network［J］.China Railway Science，2001，22(2):122－128.

［9］Liu B.Stackelberg－Nash equilibrium for multilevel programming with multiple followers using genetic algorithms［J］.Computers and Mathematics with Applications，1998，36(7):79－89.