基于时间约束的铁路空车调配系统可靠性分析

王若成

西南交通大学，交通运输与物流学院，成都 610031

0 引 言

铁路空车调配的根本任务是均衡路网空车分布，将卸车数大于装车数的站点上的多余空车合理、高效运送到装车数大于卸车数的站点，保证铁路货运系统及时、有效地完成货物装运工作。它的好坏直接影响运输工作质量和铁路运输效率，同时也间接影响整个市场的经济发展。因此，合理高效地进行空车调配作业，是提高铁路经济效益的关键。

目前，有关空车调配问题的主要研究有：Glickman[1]等根据美国铁路特点提出了以费用最小化为目标的三阶段模型；Shan[2]提出了空车调配加载能力限制，采用网络单纯形法来求解最优化问题；Mendiratt和 Turnquist[3]将空车调配问题分解为确立车辆调配规则和库存模型的两个相互关联子模型，通过确定每个车站的空车净供需，对两个模型交替求解直到得到一致最优解；Sherali和Tuncbileklz[4]提出了用来评估实际车辆规模的静态模型，以最小化车辆规模为目标，获取空车调配方案；程学庆[5]等针对铁路空车调配优化研究当中对时效性考虑不足的问题，提出建立基于时间窗(规定时间段) 和区段空车运输能力约束的空车供需平衡调配优化模型；雷中林[6]等提出以随机机会约束模型来求解铁路空车调配问题；梁栋[7]等采用动态规划方法，在空车服务时空网络模型的基础上，提出了铁路局管内空车调配的多阶段策略优化模型。刘星材[8]等提出以空车走行公里最短、到达时刻满意度最大和车种代用成本最低为优化目标，构建铁路枢纽空车调配的随机机会约束规划模型。

虽然在空车调配优化问题上国内外学者做了大量研究，但对于空车调配可靠性分析这个方面却没有引起足够的重视，国内外相关的理论研究还相对较少。铁路空车调配运输系统具有较大的随机性，在实际的空车调配过程，有大量随机、不确定因素会影响系统正常运转，这些不确定因素中，绝大部分是无法避免的，造成了铁路路网的复杂性和动态变化性，这就使得空车调配最优化模型难以取得，而系统可靠性分析可以实现对系统随机性的评估，从而解决上述问题。基于此，本文以铁路空车调配需求站（装大于卸）在规定时间内到达的空车数与需求空车数之比，作为需求站空车调配可靠性的量度，通过各需求站空车调配可靠性综合求解空车调配系统的可靠性。

1 空车调配系统可靠性模型整体思路

空车调配主要是为了均衡铁路系统空车供需不平衡，决策空车流向、流量问题。对于铁路系统中空车供应站、空车需求站的空车调配问题，其实质是决策以下两个问题：（1）空车供应站供应给空车需求站的空车数量；（2）空车供应站到空车需求站的空车运行路径。因此，铁路空车调配过程是：确定空车供需节点的空车调整量，并确定供需节点之间的OD矩阵及对应的流经线路。

铁路空车调配计划的主要目的是实现空车需求站空车的及时到发，而空车是否及时到发首先考虑的是货主的需求。鉴于货主对空车的需求有一定的时间限制，空车过早的到达会产生空车存储费用，过晚到达会使货物不能及时装运。因此，空车调配可靠性研究可以转换为在规定时间内的空车到达数是否符合空车调配计划的要求（即货主需求）。空车调配整个系统的可靠性可以转化为：利用各个空车需求站在规定时间内的空车到达率求解出整个空车调配系统的实际到达率，即整个空车调配系统的可靠性。

通过上述分析，可得空车调配的主要步骤为：

（1）根据空车调配需求分析，确立需求节点（空车需求站）、供应节点（空车供应站）之间的空车调配数量，以及供应节点（空车供应站）到需求节点（空车需求站）之间的运输径路。

（2）依照需求节点（空车需求站）货主对空车的时间要求，建立在规定时间内到达空车需求站的空车数学模型及目标函数。

（3）对建立的空车调配系统可靠性模型进行优化求解，得到空车需求站在规定时间内的到达车数。

（4）依据各空车需求站到达车数与空车调配计划到达数之比，求出空车需求站的空车到达可靠性。

（5）综合各空车需求站的空车到达可靠性，求解到达可靠性均值，该均值即为空车调配计划的可靠性。

2 可靠性模型建立

2.1 条件假设

本次建立的空车调配系统可靠性计算模型，基于如下假设：

（1）假定路段的通行能力一定，将铁路空车调配系统中的空车供应站设为起点，空车需求站设为讫点，建立相应的OD矩阵，定义铁路空车调配系统中空车流经的路径。

（2）假定在铁路空车调配系统中的车流调整都是空车调整，没有以重代空以及车种代用。

（3）假定在可靠性计算中，空车调配计划已确定，在起讫点中已包括出发作业、空车运输环节以及空车装卸作业的系统可靠性。

2.2 模型建立

假设模型中，铁路路网集合用 E表示。空车供应站共m个，空车供应站点集合表示为a={ai|i=1,2,··,m}，各空车供应节点表示为 a1,a2,··,am。空车需求站共 n个，空车需求站点集合表示为 b={bj|j=1,2,··,n}，各空车需求节点表示为 b1,b2,··,bn。

选择效益最大化作为空车调配系统可靠性模型目标函数，表示为：

ij间可选可行径路集合；以表示i-j之间可选路径中的第 k条，λ(i,j)为 i-j的可选径路总数；为决策变

量，表示空车供应站ai经第k径路运输至空车需求站 bj的空车数量(辆)；为布尔逻辑变量，用于表述示空车供应站ai经第 k径路运输至空车需求站bj的空车到达时间是否在规定时间段内，是取1，否为0。

模型是通过研究空车需求站在规定时间内的实际空车到达数与空车需求量之比，得出此次空车调配系统的可靠性，因此，需要引入一个时间变量描述空车实际到达时间，以确定空车是否在规定时间内到达指定车站。设表示空车供应站ai经第k径路运输至空车需求站bj的实际到达时间，为在路径上的空车运输时间（h），该时间可由历史运输数据估算，fi为空车供应站ai的空车出发时间（h），由上易得：

各供应站经由不同路径的发车总数与供应总数平衡，得：

各需求站经由不同路径的到达车总数与需求总数平衡，得：

设je为空车需求站bj的货主满意最早时间，jl为空车需求站bj货主满意最迟时间，该时间可在签订运输协议时由货主给出。空车在最早、最迟时间范围内到达，都视为满足了空车到达时间要求，即：

式中，ef为路段e的最大空车输送能力，eE∈。空

空车需求站的实际最大空车接收量不大于空车需求站的空车需求数，则：

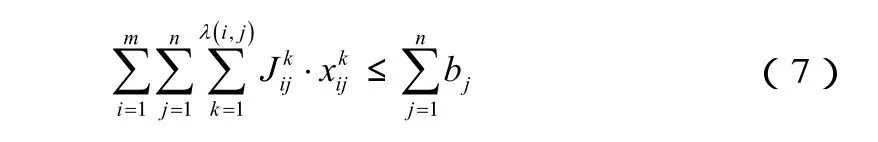
为布尔逻辑变量，需要满足如下约束：

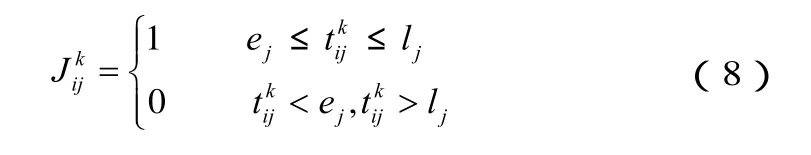
空车供应站ai经第k径路kijρ运输至空车需求站bj的空车数量(辆)k

x必须取整数：

ij

2.3 空车调配的模型可靠性

（1）各空车需求站的空车到达可靠性：

上述式子表示在货主满意的情况下（可靠时间内），由空车供应站i到空车需求站j的实际到达空车数jc与需求空车数jb的比值，就是空车调配计划中各需求站的到达可靠性。

（2）空车调配系统的可靠性

为度量系统内各站点可靠性的均值，取路网各站点可靠性的平均值为调配系统的可靠性，得：上述式子表示在货主满意的情况下（可靠时间内）整个空车调配计划中各空车需求站实际到达的空车数 与空车调配计划需求空车数 的比值。

3 算例分析

由于缺乏实际空车调配的准确数据，我们假设到达需求站的时间一致，以一个算例来论证所提出的空车调配系统可靠性的计算模型。算例背景设定如下：

选定路网的7个供需节点，其中，空车供应站3个，分别表示为a1、a2、a3；公车需求站4个，分别表示为b1、b2、b3、b4。表1为各站空车调整数量及输送时间，表2为各空车供应站的空车发出时间，表3为各空车需求站对空车到达的时间要求。

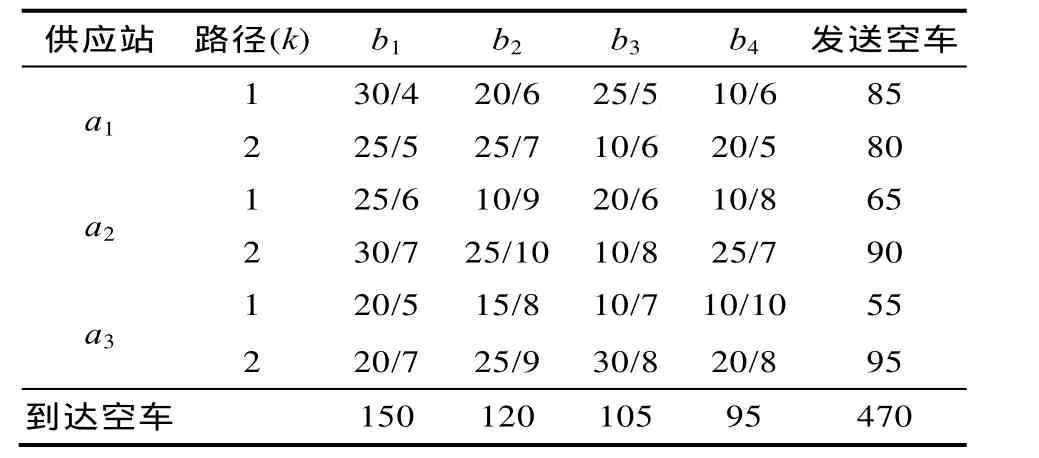
表1 各站空车调整数量及输送时间Tab.1 The adjustment number of empty wagon and the delivery time

注：“1”，“2”代表可选路径；分子代表各站到达空车数；分母代表运输时间，h。

表2 各空车供应站的空车发出时间Tab.2 The empty wagon departure time of each empty supply station

表3 各空车需求站对空车到达的时间要求Tab.3 Time demands of empty wagon arrival time for each empty demand Station

根据表1、表2、表3所给的数据，运用LINGO软件计算空车调配系统模型的最优解，如表4所示。

表4 基于空车需求站到达时间要求的最优调配空车数(辆)Tab.4 The optimal number of empty car distribution based on the demands of empty arrival time on each empty demand station

上表中，通过时间约束模型计算得出的最优空车调配方案中，各需求站的空车到达可靠性分别为：

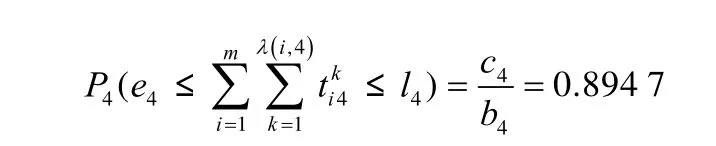
综上可知，在规定时间内空车调配系统的可靠性为：

即空车调配计划的可靠性为90.08%。

4 结 论

本文建立的基于时间约束的可靠性理论适用于求解具有动态性、模糊性的空车调配系统可靠性问题。利用各空车需求站调配可靠性求解系统可靠性，可获得简便的满意解。空车调配系统可靠性模型的建立，为研究空车调配提供了一种新的思路和求解方法。最后，使用LINGO软件进行算例分析，发现利用所建立模型分析空车调配系统的可靠性无论是在时间上还是精度上都具有显著优越性，且适用性较强。下一步的研究将放在全面考虑普通空车、车种代用与以重带空的铁路空车调配系统可靠性分析上。

[1] Glickman T. S., Sherali H. D. Large-scale network distribution of pooled empty freight cars over time,with limited substitution and equitable benefits[J].Transportation Research Part B: Methodological,1985, 19(2): 85-94.

[2] Shan Y. S. A dynamic multicommodity network flow model for real time optimal rail freight car management[R]. 1985.

[3] Mendiratta V B, Turnquist M A. Model for management of empty freight cars[J]. Transportation Research Record, 1982 (838).

[4] Sherali H D, Tuncbilek C H. Static and dynamic time-space strategic models and algorithms for multilevel rail-car fleet management[J]. Management Science, 1997, 43(2): 235-250.

[5] 程学庆, 陆一新, 尹传忠, 等. 基于时间窗的铁路空车调配优化模型及求解[J]. 中国铁道科学, 2008,28(6): 113-116.

[6] 雷中林, 何世伟, 宋瑞, 等. 铁路空车调配问题的随机机会约束模型及遗传算法[J]. 铁道学报, 2006,27(5): 1-5.

[7] 梁栋, 林柏梁. 铁路空车调配的多阶段策略优化模型研究[J]. 铁道学报, 2007, 29(1): 1-6.

[8] 刘星材, 何世伟, 孙杨, 等. 基于时间满意度的铁路枢纽空车调配随机机会约束模型及算法研究[J].铁道学报, 2013, 35(9): 1-6.