频率对二维声子晶体平板负折射成像的影响

刘绍娥，贺萌，覃世冬，李晓春, ，周科朝，黄伯云

(1. 中南大学 物理科学与技术学院，湖南 长沙，410083；2. 中南大学 粉末冶金研究院，湖南 长沙，410083)

左手物质的概念最早由 Veselago于 1968年提出[1]。在Veselago的理论中，介电常数ε和磁导率μ同为负数，其折射率n也为负数，由此引发负折射效应。但是，由于自然界不存在天然的左手物质，Veselago的理论在很长一段时间内都没有受到足够的关注，负折射的研究也进展甚微。直到1996年，Pentry等[2]从理论上证明了用周期性排列的金属条和金属开口谐振环组成的复合结构，在一定频率范围内能够产生负等效介电常数和负等效磁导率。之后，Smith等[3]制作了世界上第一块等效介电常数和等效磁导率同时为负的介质；Shelby等[4]则首次在实验上证明了当电磁波斜入射到左手介质和右手介质的界面时，折射波的方向与入射波的方向位于法线的同侧。这些研究引起了人们的广泛关注。Pentry[5]关于负折射平板可以突破衍射极限完美成像的理论建议更是激起了研究者们的极大兴趣。而且，人们找到了一种现实有效的实现负折射的方法，那就是利用人工结构——光子晶体[6-8]。随着研究的深入，负折射研究已扩展到了声子晶体领域[9-13]。在解释声子晶体平板负折射成像时，通过引入等效负折射率概念，并利用反常折射定律来描述成像过程[14-15]。在此，本文作者在考察声子晶体等效负折射率的等效范围的基础上，从声波频率和入射角两方面，对声子晶体平板成像特性进行分析。

1 理论与模型

以二维钢/空气声子晶体为模型，垂直方向的钢圆柱以正三角结构排列于空气中。材料参数为：对于空气，密度ρ=1.29×10-3kg/m3，纵波波速cl=0.34×10-3m/s，横波波速ct=0 m/s；对于钢柱，ρ=7.67×103kg/m3，cl=6.01×103m/s，ct=3.23×103m/s。钢柱的半径r=0.36a(a为晶格常数)，对应的单胞填充率为f=0.47。用多重散射方法计算模型能带结构，结果如图 1(a)所示。图1(a)中，从Γ点出发的直线表示空气的色散线。从图 1(a) 可以看出：在归一化频率(简称为频率，下同)为 0.62～0.95时，Γ点的频率比其他点的频率都要高，说明在该频段内，等频线的梯度方向是指向Γ点的，即群速度方向和波矢量方向相反。因此，该频段就是发生负折射现象的区域。图1(b)所示为等频线图，可见：当频率达到0.62时，等频线凹向Γ点，与带结构图中的提示一致。

从图1(b)可以看出：不同频率对应的等频线具有不同的形状。等频线是声波在声子晶体中传播特性的反映。对于本文中的模型，在频率0.65～0.95之间等频线的形状近似为圆形。这意味着这些频率的声波沿声子晶体各个方向的传播特性相同，即各向同性。因此，可用等效负折射率的概念来描述该声子晶体中的负折射行为。

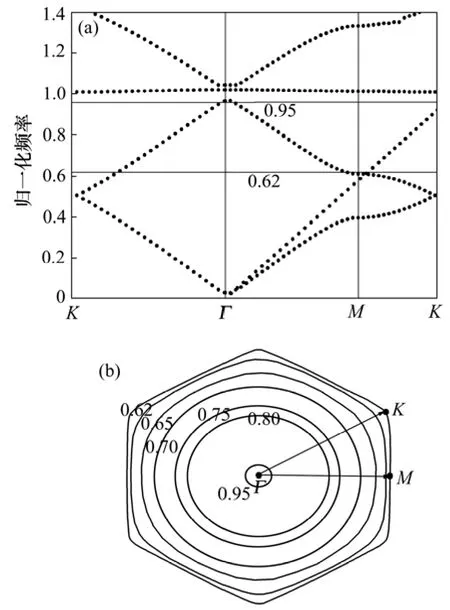
图1 二维三角steel/air声子晶体能带结构和等频线Fig.1 Band structure for phononic crystal consisting of steel cylinders hexagonal arranged in air background and equifrequency surfaces for some frequencies

根据声子晶体等效负折射率的定义[13]，结合等频线理论，用多重散射方法计算本文模型的等效负折射率，结果如图2(a)所示，其中，在频率0.65～0.80之间为圆形等频线对应的频率范围。从图 2(a)可以看出：随着入射波频率增大，本文模型的等效负折射率的绝对值逐渐减小。等效负折射率的这种变化将直接影响声子晶体平板负折射成像，并会造成类似几何光学成像中的色像差，即‘点’物成‘线’像。

本文模型中，基体材料为空气，若其折射率记为1，则折射规律可写为。其中：iα和rα分别为入射角和折射角；neff为声子晶体相对于空气的等效负折射率。显然，折射角rα的取值范围为0°～90°。因此，对于任意一个等效负折射率neff，当rα=90°时，都存在1个最大入射角。只有入射声源的入射角小于时，声波才会在声子晶体表面发生负折射行为，即入射角在αi,MAX内的信号才会对负折射成像有贡献。由于等效负折射率会随入射波频率的变化而发生改变，因此，也会受入射波频率的影响。图2(b)所示为与入射波频率之间的变化关系曲线。从图2(b)可以看出：随着频率的增大，逐渐变小。同时，能发生负折射现象的入射角范围也相应减小，进而影响负折射成像，即出现频‘高’像‘暗’现象。以下通过数值模拟来说明这些现象。

图2 声子晶体等效负折射率随频率的变化关系和最大入射角随频率的变化关系Fig.2 Effective negative refractive index vs frequency and maximum incident angle vs frequency

2 入射角对负折射的影响

以9层声子晶体平板为模型，模拟高斯波束以不同角度入射声子晶体平板后的折射现象。入射的高斯波频率为0.70，由图2(b)可知：该频率对应的αi,MAX为32.57°。图 3所示为入射角分别为 20.00°，32.57°和40.00° 3种情况下的平板负折射过程。图3～6中水平(x)和垂直(y)方向刻度均表示空间位置，a为晶格常数。图3～6中的灰度由黑至白，表示声压逐渐增强。

由图3可知：入射角小于αi,MAX如 20.00°时，平板中出现明显的负折射情况(见图3(a))；当入射角大于αi,MAX如40.00°时，无负折射情况出现(见图3(c))；入射角等于αi,MAX如32.57°时，负折射情况处于边界状态(见图 3(b))。因此，高斯波在平板中的折射过程证实了αi,MAX的存在。

αi,MAX的存在也会影响平板负折射成像。在点声源平板负折射成像中，表现为：不同的入射角范围内的信号对像的贡献不同。仍以9层声子晶体平板为例，点声源频率保持为0.70，点声源离声子晶体平板的距离为10.0 (即物距)。在确定的物距下，通过在平板前加挡板的方式，控制入射到平板的入射角范围。图 4所示为不同的入射阻挡下，平板负折射成像的结果。

图 4(a)中：点声源发出的声波信号没有受到任何阻挡，全部通过声子晶体平板负折射成像；在声子晶体平板的内部和外部出现完整、清晰的汇聚像点。图4(b)中：与水平方向夹角在±16.28°之间的入射声波信号被阻挡，相当于±αi,MAX/2内的信号被挡，只有入射角绝对值在16.28°到αi,MAX之间的入射信号通过平板，产生了负折射；因此，像的强度受到了较大影响，像变得模糊、暗淡了许多。图4(c)中：与水平方向夹角在±32.57°之间的入射声波信号被阻挡，相当于±αi,MAX内的信号都被隔板挡住，即可以产生负折射的入射信号都被阻挡。因此，图 4(c)中：平板负折射成像不见了。这进一步说明：只有入射角小于αi,MAX的声波信号才能通过平板负折射成像，而其他的入射信号对负折射成像没有贡献，或贡献几乎可以忽略。

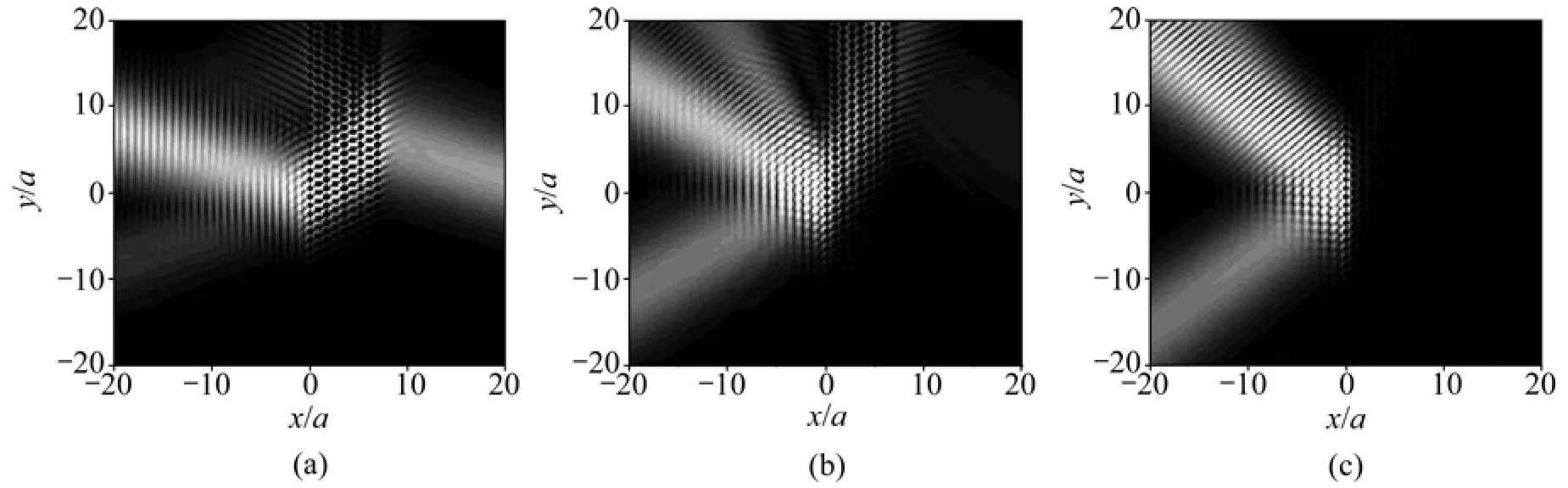
图3 频率为0.70的高斯波经9层声子晶体平板折射的声场分布Fig.3 Intensity distributions of pressure field of Gaussian Beam across nine-layer phononic crystal slab

对同一入射角、不同的物距，声源投射到平板上的面积不一样。物距小的，投射到平板上的面积小；物距大的，投射到平板上的面积也大。当αi,MAX固定为 32.57°，物距分别为2.6，6.6和10.6时的成像如图5所示。平板宽度仍为9层，入射频率保持0.70。

比较图5(a)，5(b)和5(c)中3个不同物距条件下的成像特征，除了由于物距的变化，成像位置会出现相应的平移外，还发现：随着物距的增大，竖直方向(y方向)上发生负折射的范围变宽，但像的强度及清晰度几乎没有改变。这主要是因为αi,MAX固定，即使投射到平板的面积增大，但不增加折射进入声子晶体平板的声波信号，故像的强度不变。图5所示的结果进一步证实了前面关于入射角影响成像的判断。

3 入射频率对成像的影响

以0.05为间隔，选取0.65～0.75之间的3个频率点作为入射点声源的频率，利用多重散射方法，模拟点声源经9层声子晶体平板的负折射远场成像情况，结果见图6。图6中声子晶体平板的填充率仍为0.47，物距保持为10.0。

由图6可知：入射声源频率改变，像的位置、强度、清晰度都发生改变。具体表现为：随着点声源频率的增加，声子晶体平板外部的成像离平板右端面(出射面)的距离增大；像的强度逐渐减弱，“线状像”的清晰度也随之降低，平板内部的汇聚点离平板左表面的距离减少。另外，当声源频率增大时，声波在声子晶体平板左表面的有效投射面积变小。

负折射成像随声源频率变化的这些现象，可以用等效负折射率的特性及折射定律加以解释。一方面，随着入射频率的增大，等效负折射率的绝对值减小(见图2(a))，这样，对于一定的小角度入射信号，根据折射定律，对应的折射角增大，从而导致声子晶体平板内部像点位置向平板的左表面(入射面)移动，相应地就有平板外部的像点位置朝远离声子晶体平板的方向移动；另一方面，随着入射声源频率增大，能发生负折射的最大入射角αi,MAX减小(见图 2(b))，有效投射面积变小，耦合进入声子晶体平板的声波信号减弱，从而导致平板外部成像的强度减弱，像也变得模糊。

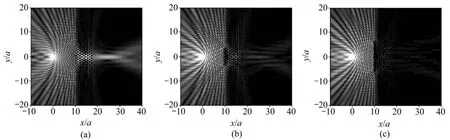
图4 不同入射角范围对应的点声源负折射成像图Fig.4 Negative refractive imagings of point source with different incident angle ranges

图5 物距变化时的平板负折射成像Fig.5 Negative refractive imagings of phononic crystal slab with change of distance between point source and phononic crystal slab

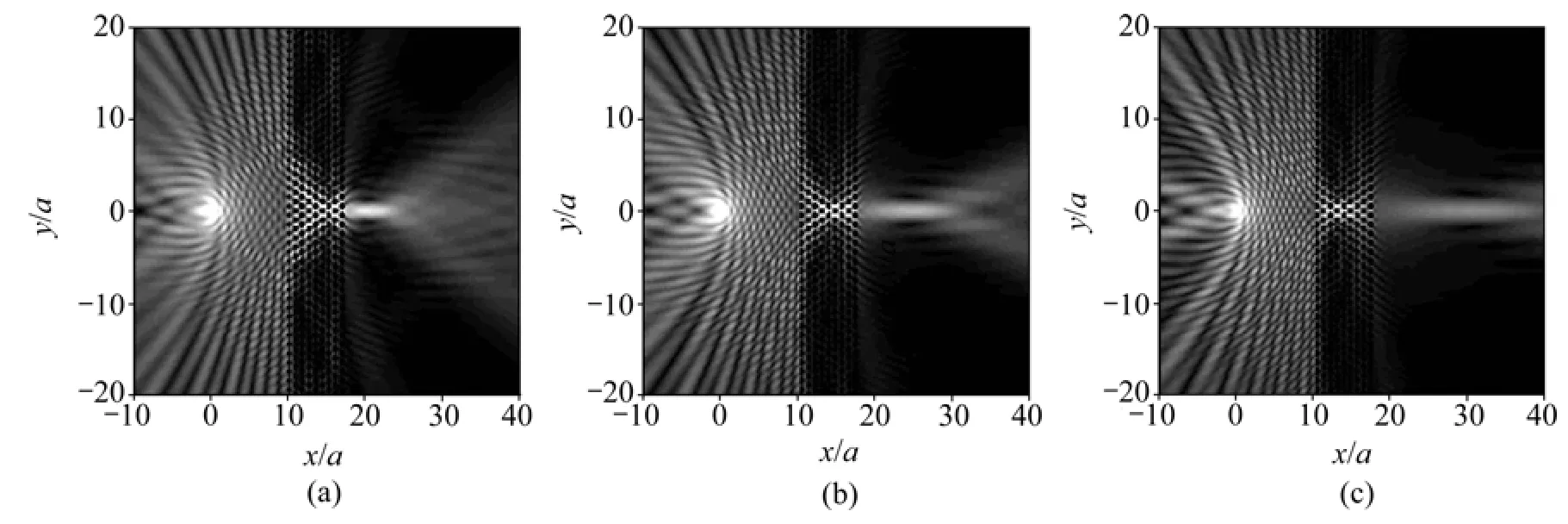
图6 不同频率信号的负折射成像Fig.6 Negative refractive imagings of sound signals with different frequencies

4 结论

(1) 声子晶体的等效负折射率，其绝对值随声源频率的增大而减小，平板负折射也会出现类似几何光学成像中的色像差；对于某一确定的入射声源频率，负折射现象存在一个最大入射角，且随着声源频率的增加，这一最大入射角变小。

(2) 在声子晶体平板负折射成像过程中，点声源的频率不仅会影响负折射成像的位置，还会影响像的强度和清晰度。随着点声源的频率的增大，最大入射角变小，负折射进入声子晶体平板的有效声波信号减弱，负折射成像的清晰度降低。

(3) 在应用平板负折射成像的实际过程中，应根据成像所用到的频率，选择合适的物距和入射角，以得到清晰明亮的像。或者选择合适的信号频率、合适的物距，以达到清晰成像的目的。

[1] Veselago V G. The electrodynamics of substances with simultanously negative values ofεandμ[J]. Sov Phys Usp, 1968,10(4): 509-514.

[2] Pentry J B, Holden A J, Stewart et al. Extremely low frequency plasmons in metallic mesostructures[J]. Phys Rev Lett, 1996,76(25): 4773-4775.

[3] Smith D R, Padilla W J, Vier D C, et al. Composite medium with simultaneously negative permeability and permittivity[J]. Phys Rev Lett, 2000, 84(18): 4184-4187.

[4] Shelby R A, Smith D R, Schultz S. Experimental verification of a negative index of refraction[J]. Science, 2001, 292(5514):77-79.

[5] Pentry J B. Negative refraction makes a perfect lens[J]. Phys Rev Lett, 2000, 85(18): 3966-3969.

[6] Notomi M. Theory of light propagation in strongly modulated photonic crystals:Refraction like behavior in the vicinity of the photonic band gap[J]. Phys Rev B, 2000, 62(16): 10696-10705.

[7] Cubukcu E, Aydin K, Ozbay E, et al. Negative refraction by photonic crystals[J]. Nature, 2003, 423(5): 604-605.

[8] Schonbrun E, Yamashita T, Park W, et al. Negative-index imaging by an index-matched photonic crystal slab[J]. Phys Rev B, 2006, 73(19): 195117-195122.

[9] YANG Su-xia, Page J H, LIU Zheng-you, et al. Focusing of sound in a 3D phononic crystal[J]. Phys Rev Lett, 2004, 93(2):24301-24304.

[10] FENG Liang, LIU Xiao-ping, LU Ming-hui, et al. Acoustic backward-wave negative refractions in the second band of a sonic crystal[J]. Phys Rev Lett, 2006, 96(1): 14301-14304.

[11] ZHANG Xiang-dong. Universal non-near-field focus of acoustic waves through high-symmetry quasicrystals[J]. Phys Rev B,2007, 75(2): 24209-24212.

[12] Sukhovich A, LI Jing, Page J H. Negative refraction and focusing of ultrasound in two-dimensional phononic crystals[J].Phys Rev B, 2008, 77(1): 14301-14309.

[13] HE Zhao-jian, HENG Yao-fu, PENG Sha-sha, et al. Acoustic collimating beams by negative refraction in two-dimensional phononic crystal[J]. Journal of Applied Physics, 2009, 105(11):116105-116107.

[14] LI Jen-sen, Chan C T. Double-negative acoustic metamaterial[J].Phys Rev E, 2004, 70(5): 55602-55605.

[15] QIU Chun-yin, ZHANG Xiang-dong, LIU Zheng-you. Far-field imaging of acoustic waves by a two-dimensional sonic crystal[J].Phys Rev B, 2005, 71(5): 54302-54307.