基于Matlab的数控加工曲线拟合算法*

赵敬云，王鹏飞

(河南机电高等专科学校，河南新乡453000)

1 引言

当前数控加工过程中，数控程序的编制方法有手工编程和自动编程两种。手工编程过程依靠技术人员或者机床操作人员的经验编写数控程序，面对待加工对象，直接编程。适合一些形状简单，特别是点位加工的工序，程序简单，处理简便。自动编程完全依靠计算机自动完成编程工作，设计人员只需将所设计的零件或者设计的源程序通过数据交换导入到自动编程软件中。由计算机自动地进行处理，计算出刀具中心的轨迹，编写数控加工源程序。对于轮廓比较复杂、形状不是简单曲线的零件，往往需要数控后处理软件进行数据处理，自动生成数控程序。自动编程程序一般带有刀具轨迹仿真功能。但此功能仅仅是加工结果的数字显示，不能对处理过程干涉，也不能决定加工处理的数据。因此对于一般曲线自动编程过程中，曲线处理精度、曲线处理方法完全由自动编程软件控制，设计人员无法对处理过程干涉。在数据处理过程中，可能造成简单曲线过度处理，运算效率过低，而对于复杂曲线，运算精度又无法控制，无法达到运算要求。

数控加工曲线拟合算法的设计思想如图1所示，直接将加工轮廓划分为小的曲线段，根据数控加工的要求，把这些曲线段用较小直线、圆弧段拟合，只需解出圆弧段和直线段的端点数据，则预加工曲线能够生成加工程序。生成数控程序之前利用Matlab分析设计结果。如果加工程序不能满足设计要求，可对处理曲线重新拟合。这样设计结果可供设计人员控制，提高了数控加工精度。

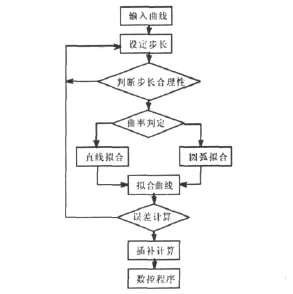
图1 曲线拟合加工流程图

2 加工曲线分段处理

数控后处理程序对曲线加工编程过程中，曲线分析的第一步骤应该是判断加工曲线的特殊点，也就是说待加工曲线的转折点。如图2所示，刀具容屑槽加工时，该容屑槽加工曲线由三段曲线组成。刀具的切削部分和刀具背部为曲线，容屑槽底部为一直线段，如果把该曲线作为整体数控编程，曲线会变得异常复杂，只有采用高次曲线模拟才能实现曲线拟合，而且曲线拟合的精度不好控制。因此加工曲线转折点的判断是非常重要的过程，关系到曲线拟合精度。而传统的曲线编程转折点的参数通常用手工计算，或者用图解确定，从而降低了计算精度和效果。

本文提出的计算方法，首先找到曲线的转折点，然后再将刀具廓形划分成m个单元几何段，每个几何段用光滑线段(直线或圆)拟合，划分为m个单元几何段之后，会得到2m个端点，将这2m个端点分别求解，并找出每段曲线的切入点角度。将这2m个端点x，y及角度数据列为3×2m的矩阵。这样每个接合处就有两个点:上一段末点和本段首点。对于无转折点的曲线，这两点x，y坐标及切入点角度完全相同。对于有转折点的加工曲线，两个转折点的x，y相等，但是切入点角度存在夹角。这样加工曲线的转折点就找到了。

图2 面铣刀容屑槽加工曲线

加工曲线转折点找到之后，对原曲线进行离散，将所有的几何段分别按照曲率判断该曲线段适合直线拟合还是圆拟合，将所有的曲线段分别用拟合曲线替代，最后将拟合曲线与原曲线进行误差分析，如果误差超出机床脉冲当量。需要重新对原曲线计算。如果超出设计精度，可以直接输出数控代码。

3 加工曲线拟合运算

曲线分段之后，每段曲线的端点用三个参数代表:横坐标xij、纵坐标yij和角坐标αij，其中角坐标为点Fij处横坐标轴的切线或纵坐标轴的法线斜角αij。加工曲线分段后以三维数组表示，即:

这样描述适合于计算机处理。

3.1 直线段轮廓计算

点F1j是pj段的起点，而Fkj是它的终点;坐标x1j和y1j是第一个点，而最后一个点坐标xkj和ykj认为是已知的。点 Fij的参数 xijyijαij的值为:

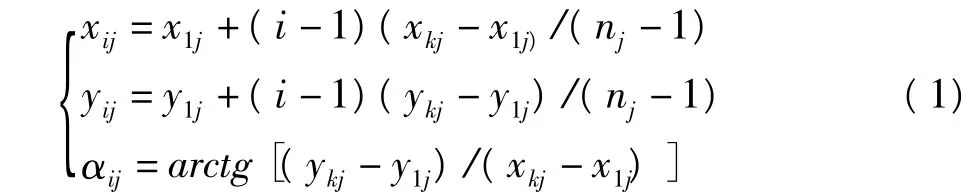
Matlab绘制直线程序为:

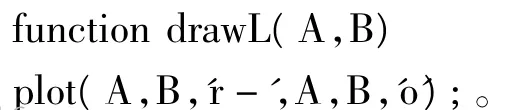
3.2 圆弧段轮廓计算

将圆弧中心角θj分成nj－1部分，可以求出圆弧段初终点间极角差。将刀具廓形圆弧段圆心为极点建立极坐标系，用来精确地确定点Fij极角τij值。

知道弧形圆弧段第一个点和最后一个点的坐标后，就可以计算极角 τij和 τkj。

取段Pj上有nj个点(包括边缘)，则极角τij=τ1j+(i－1)△θj

就得到基本坐标系xoy中计算段上点的坐标。

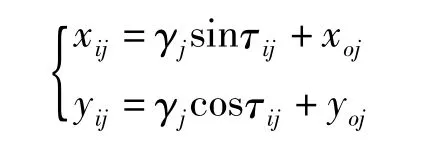
圆弧拟合子程序:

4 加工曲线拟合应用

为了验证拟合结果，采用matlab编程得到一标准正弦曲线，将正弦曲线按照程序进行离散，离散的主程序如下所示。图3为拟合结果，图4为拟合前后的对比图。从图4可以看出，拟合结果跟原曲线吻合度很好，以正弦曲线分析可以拟合相适度可以达到98%以上。

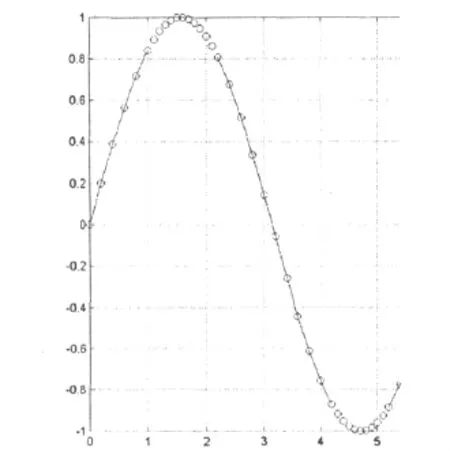
图3 正弦曲线拟合图

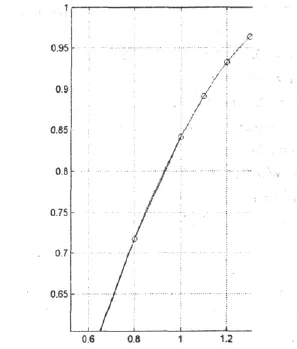
图4 局部细节对比图

5 结论

数控加工曲线的拟合算法是数控切削加工计算的一种尝试。曲线离散拟合算法减少了一般曲线数控编程的中间环节，而且编程过程中设计人员可以随时对设计结果进行干预，直接得到数控代码。这种算法具有通用性和实用性，曲线的编程方法即可用于零件加工，也适用于成形刀具加工。对于成形刀具设计时解决刀具廓形逆向反求问题时应用最多。

利用曲线离散设计数控加工曲线时，可以利用Matlab编写计算机程序，解决了曲线编程中大量的计算工作量，防止加工过程中廓形参数不确定出现的错误。

［1］ 刘桂明，刘峰，郭庆祥.成型刀具在回转体及骨架式轴唇圈橡胶模加工中的应用［J］.模具制造，2005，(3):68 －70.

［2］ 陈刚.铲磨成型刀具的计算机辅助制造［J］.工具技术，2005，(4):58－59.