额定风速以下风力发电系统的双频环优化控制器设计

陈 奇，桑英军，王林高

(淮阴工学院，江苏淮安223003)

0引 言

风力发电系统是一个大范围强风速扰动的强非线性系统，而目前许多控制方法都是以工作点附近线性化模型为基础设计的［3］，在系统工况点附近小范围扰动时，控制器具有较好的控制性能，但系统工况点是随来流风速的变化而变化的，风速的随机性导致了风力发电系统的线性化模型精度不高，因此有必要根据风速的特点，建立起合适的风电系统模型。有学者根据风速的特性，将风速考虑为缓慢变化的低频风速和快速变化的高频风速的叠加［4］，其中低频部分是风速长时间尺度的、低频的变化量，高频部分是风速脉动的部分，是风速短时间的、高频的扰动量，并由此提出风力发电系统的双频模型［5］，该模型考虑了风速的特点，不仅可以保证控制精度，而且避免了大量计算。

额定风速以下时，风力发电系统的基本控制目标有两个，一是实现最大风能捕获，二是尽量降低系统的电磁转矩振荡，这些控制目标涉及到优化控制问题［6］。目前，H∞鲁棒控制理论是一个发展比较完善的理论体系，其设计过程考虑了数学模型所具有的不确定性，不依赖于被控对象的精确数学模型，设计的控制器能够使系统对不确定性误差范围内的所有被控对象都满足性能指标要求［7］。此外，On-Off控制方法也得到了广泛应用，该方法通常在低功率的风能转换系统中使用，能够对低频风速变化做出快速的反应，对于风力发电系统固有的参数不确定性具有很好的鲁棒性［5，7］。已有学者将上述两种方法分别应用于风力发电中。

本文首先建立风力发电系统的双频模型，分别针对低频和高频子模型设计优化控制器，其中低频环采用On-Off优化控制方法，高频环采用H∞动态输出反馈控制方法，通过选取不同的H∞性能指标进行仿真研究。结果表明，基于H∞动态输出反馈控制的风力发电系统双频环优化控制方法是有效的。

1系统建模

变速恒频风力发电系统结构框图如图1所示。风轮转动将风能转换成机械能，经传动系统带动发电机转子旋转发电，机械能转换为电能，最终经交直交变换器输送到电网中。

图1 变速恒频风力发电系统结构图

1．1 风速模型

根据风速的特点，文献［4，5］将纵向风速看作由两部分组成:

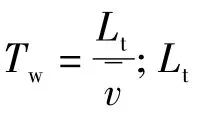
1．2风力机模型

根据贝兹理论，风力机产生的机械力矩:

1．3传动系统模型

传动系统将低速风轮转速转换为高速电机转速，主要由增速齿轮实现，忽略粘性摩擦，其运动方程如下［5］:

式中:ωh为电机转子转速;i为齿轮变比;ΓG为电机电磁转矩;η为齿轮效率;Jl为传动系统低速轴的总转动惯量。式(3)和式(5)组成了风力发电系统的基本非线性模型。

1．4 双频模型

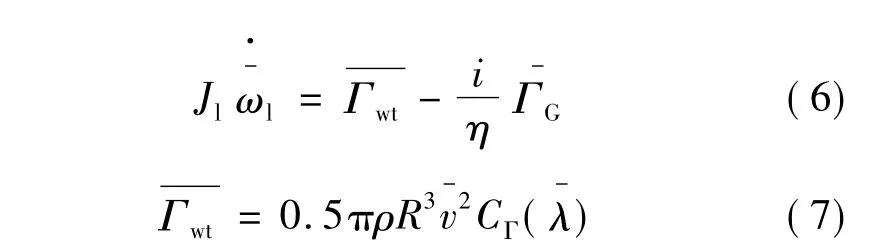
采用文献［5］的方法，得到风力发电系统的高频子模型:

2双频环优化控制

额定风速以下时，风力发电系统的控制目标如下:(1)控制发电机转速，实现风速缓慢变化的低频部分的最大风能捕获，即叶尖速比λ快速跟踪其最优值λopt，功率系数Cp达到最大值;(2)抑制风速快速变化的高频扰动部分造成的电磁转矩振荡，尽量使发电机机械振荡最小，保障系统运行的可靠性。

2．1低频环On-Off控制

图2 低频环On-Off优化控制结构

2．2高频环H∞动态输出反馈控制

则高频子模型可以重新写为:

本文要设计的动态输出反馈控制器为u=K(s)y，其状态空间表示形式如下:

式中:ζ 是控制器的状态，;Ak、Bk、Ck、Dk是待确定的控制器参数矩阵。

由此，高频环的控制目标可以描述如下:设计控制器式(11)，使得由式(10)和式(11)组成的闭环系统满足如下鲁棒H∞性能［8］:

(1)当外部干扰e(t)=0时，闭环系统是渐进稳定的;

(2)对给定的γ∞＞0，从 e(t)到 z∞的闭环传递函数矩阵 Tez∞(s)满足‖Tez∞(s)‖∞＜ γ∞。

为求解输出反馈控制器的参数矩阵，给出如下定理:

则控制器式(11)使得由式(10)和式(11)组成的闭环系统稳定，同时使其闭环传递函数满足‖Tez∞(s)‖∞＜γ∞。

式(2)中，*表示由矩阵的对称性得到的矩阵块。

根据以上定理，可以按如下步骤设计所需的输出反馈控制器。

(2)求满足MNT=I-XY的矩阵M和N，即对I-XY进行奇异值分解即可。

(3)利用式(14)求出控制器参数矩阵。

图3 双频环优化控制结构

3仿真分析

为验证本文提出控制方法的有效性，在Matlab/Simulink环境下建立起风力发电系统及控制器的仿真模型，仿真参数如表1所示［5］。得到的风速仿真波形如图4所示。

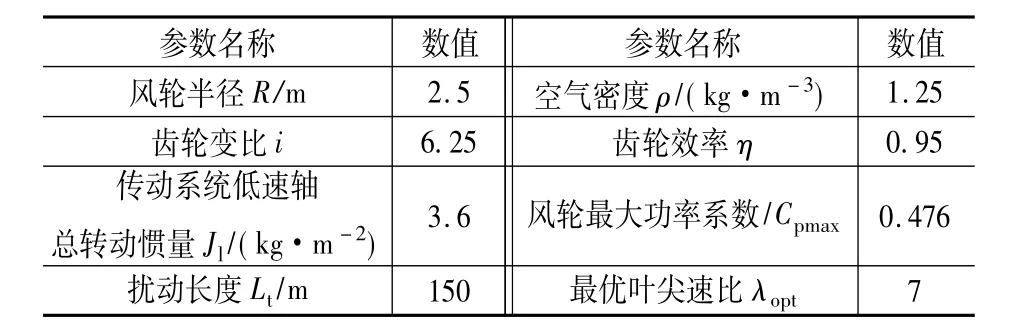
表1 仿真参数

图4 风速仿真波形

选取不同的H∞性能指标γ∞，利用LMI工具箱中的求解器求解定理1，进而得到控制器参数矩阵Ak、Bk、Ck、Dk:

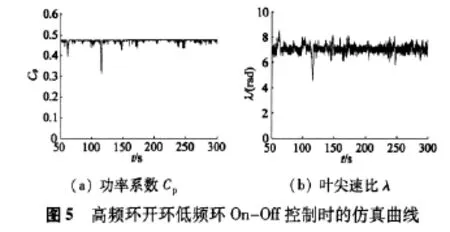
为验证风力发电系统双频环优化控制方法的有效性，首先将高频环做开环处理，只保留低频环部分，此时系统的参考转矩 ΓGref=ΔΓGref，取 γ∞=0．01时的控制矩阵进行仿真，得到的仿真结果如图5所示。

然后高频环加入H∞动态输出反馈控制进行仿真，得到双频环优化控制的仿真结果如图6所示。

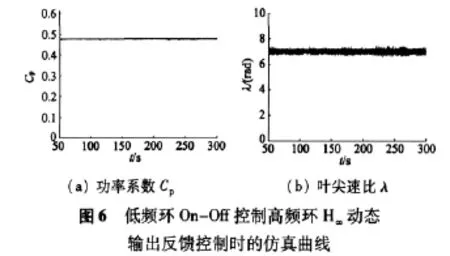
从仿真波形可以看出，功率系数Cp(λ)和叶尖速比λ都以不同的程度接近其最优值。其中功率系数Cp(λ)采用文献［5］中方法，由如下多项式得到:

由该式可知，当λ=7时，Cp(λ)达到最大值，即Cpmax(λ)=0．476，此时风能的捕获率最大。对于单纯的On-Off控制，高频环加入H∞动态输出反馈控制后，功率系数Cp变得更加平稳，更接近其最大值 Cpmax(λ)=0．476;(t)跟踪 λopt得精度变得更高，系统的鲁棒性变得更好。这表明基于H∞动态输出反馈的双频环优化控制方法是有效的。

由前述风力发电系统总的控制目标可知，不仅要使低频风能的捕获率最大，还要抑制过大的电磁转矩振荡。为了对两者进行仿真比较，分别选取γ∞=0．01和γ∞=1所对应的控制矩阵进行仿真，得到如图7、图8仿真结果。

从仿真波形可以看出，γ∞=0．01时，功率系数Cp的响应波形比γ∞=1时的平稳，但电磁转矩归一化误差的波形要比后者振荡严重，这表明风力发电系统的控制目标之间是相互影响的，要综合考虑对其进行折衷处理，在系统实际运行过程中，应根据具体的控制目标适当选取γ∞，使系统更加符合运行要求。

4结 语

根据风速的特性，将风速考虑为缓慢变化的低频风速和快速变化的高频扰动风速的叠加，在此基础上建立了风力发电系统非线性双频模型。本文分别针对高频风速和低频风速设计了双频环优化控制器，由低频On-Off控制部分和高频H∞动态输出反馈部分组成。仿真结果表明，本文提出的风力发电系统的双频环优化控制方法能够很好地跟踪控制目标，减小振荡，使系统获得更好的鲁棒性能。但最大化捕获低频风能与抑制高频振荡这两个目标之间是相互影响的，可通过选取不同的H∞指标，在多个控制目标之间得到不同程度的折衷。例如，若控制目标侧重于最大风能捕获，可选取较小的γ∞;若控制目标侧重于保障系统的可靠运行，可选取较大的γ∞。

［1］ 李俊峰，石鹏飞，高虎．中国风电发展报告2010［R］．海口:海南出版社，2010．

［2］ 张运洲．如何实现非化石能源消费比重11．4%目标［N］．经济参考报，2011-4-11(6)．

［3］ Steinbuch M．Dynamic Modeling and Robust Control of Wind Energy Conversion System［D］．PhD Thesis，Delft University of technology，The Netherlands，1990．

［4］ 李东东，陈陈．风力发电系统动态仿真的风速模型［J］．中国电机工程学报，2005，25(21):41-44．

［5］ Munteanu I，Brarcu A I，Cutululis N A，et al．Optimal Control of Wind Energy Systems［M］．London:Springer，2008．

［6］ 李元龙，朱芸，纪志成．风能转换系统优化控制策略综述［J］．微特电机，2009(2):59-63．

［7］ 张先勇，吴捷，杨金明，等．额定风速以上风力发电机组的恒功率H∞鲁棒控制［J］．控制理论与应用，2008，25(2):321-328．

［8］ 王美，张宵力．一类不确定切换系统的鲁棒H∞动态输出反馈控制器设计［J］．福州大学学报(自然科学版)，2008，36(S):125-129．

［9］ 俞立．鲁棒控制--线性矩阵不等式处理方法［M］．北京:清华大学出版社，2002:44-58．