基于RBF网络的开关磁阻电动机自适应滑模控制

周素莹，林 辉

(西北工业大学，陕西西安710072)

0引 言

开关磁阻电动机(以下简称SRM)因结构简单、坚固，制造成本低，调速范围宽及效率高等优点，成为可变速驱动系统中极具潜力的新成员。然而，其定子、转子的双凸极结构及开关形式供电电源，使得开关磁阻电动机驱动系统(SRD)成为一个多变量高度耦合、非线性严重的系统，解决SRM的非线性耦合问题是实现SRM高性能控制的关键。

本文将滑模变结构控制对系统参数摄动及外部干扰的不变性和径向基函数神经网络能够任意精度逼近任何单值连续函数的特性相结合，采用RBF神经网络在线估计SRM的结构参数，实现了基于反馈线性化的SRM滑模控制。仿真研究证明了所提出方法的有效性。

1 SRM的非线性数学模型［1-2］

SRM用状态方程表示，则为一个高阶的非线性系统。根据SRM的运行特性，其状态方程:

式(2)中ψs为饱和磁链，函数fj(θ)表示:

在不饱和条件下的相电感Lj(θ)可表示为:

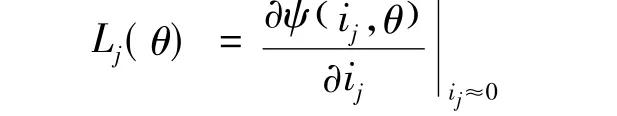
由此可得到:

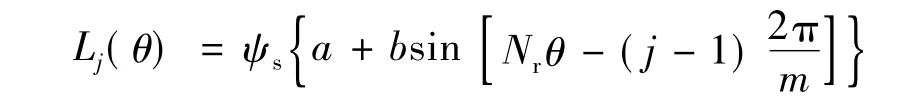
其中a、b可根据对齐位置和非对齐位置的电感值La和Lu进行计算。为便于计算，这里定义:

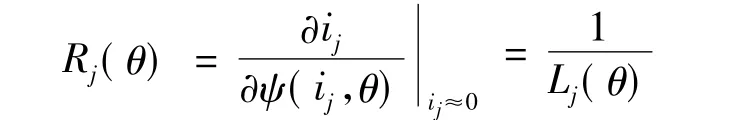
相电流可表示为:

电机一相产生的转矩:

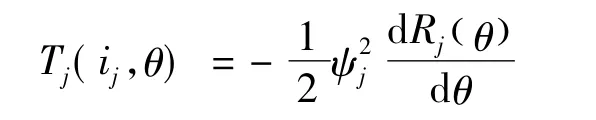
m相电机产生的总转矩为:

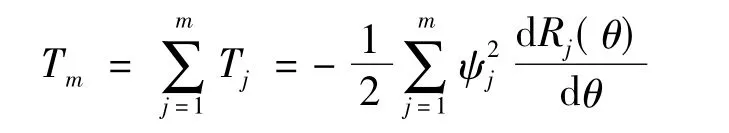
因此可得到如下:

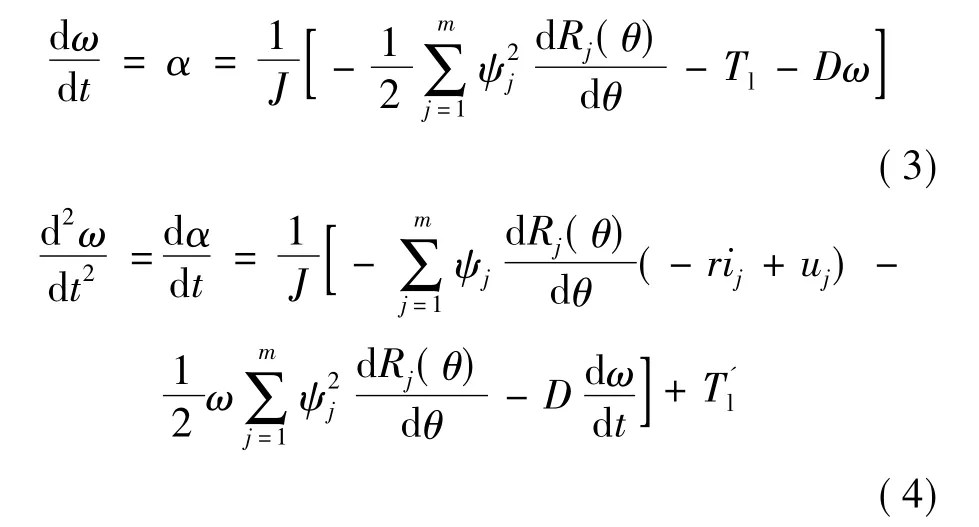
表示功率变换器通断的变量kj定义如下:

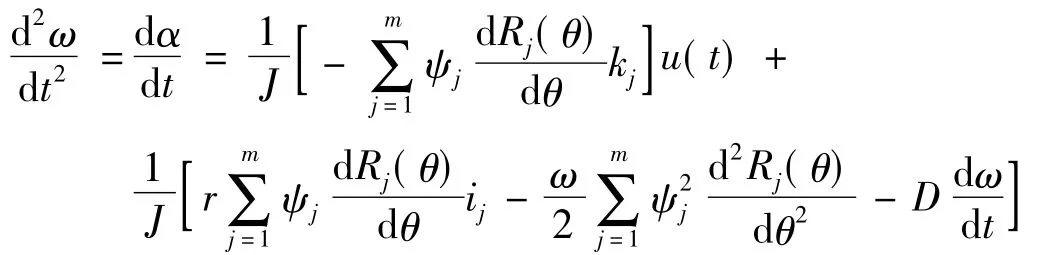
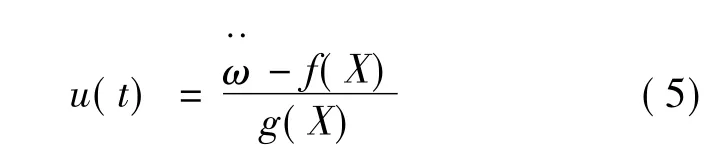
2基于RBF网络的自适应滑模控制器设计

图1 开关磁阻电动机自适应神经滑模控制结构图

2．1 SRM自适应神经滑模控制器设计

2．1．1切换函数及控制律的设计

(1)切换函数的选取

滑模变结构切换函数维数一般等于控制矢量的维数，故选取滑模切换函数:

根据线性化反馈技术［4-5］，可将滑模控制律设计:

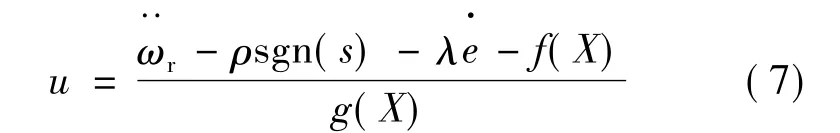
为减小切换控制量的幅值，采用等效控制法，即滑模控制输入的结构:

式中:ueq为等效控制部分。usw为滑模切换控制部分，是通过高频切换控制使系统状态趋向滑模线，并保证状态沿着滑模线滑向稳态点，使系统具有很强的鲁棒性。

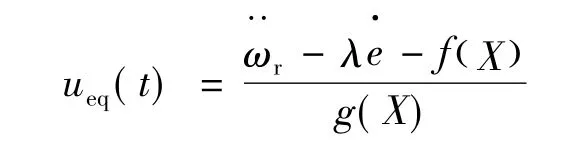
切换控制器可设计:

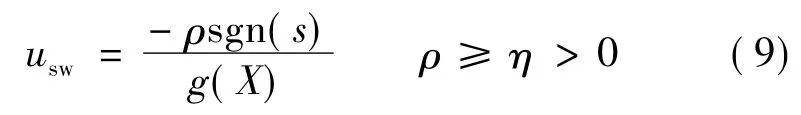
(2)滑模控制器的稳定性分析

定义Lyapunov函数:

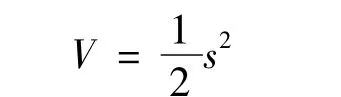
把式(9)代入得:

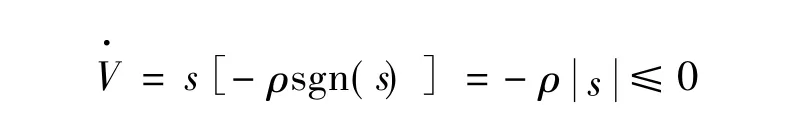
由上述证明可知该系统能够稳定，即所设计的等效控制器设计能够满足闭环控制系统的稳定性。

2．1．2基于RBF网络的电机参数函数的逼近

由于开关磁阻电动机参数的高度非线性，以及电机运行时参数变化和扰动的影响使得难以精确求出式(7)的控制律，为此对电机参数进行实时辨识，采用控制的方法精确逼近实际的电机结构参数显得尤为重要。

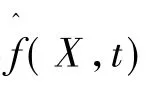
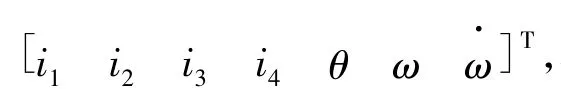
依据切换函数式(6)，有:

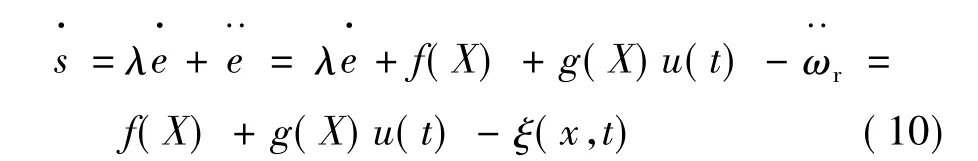
设在时刻t时的网络输出:

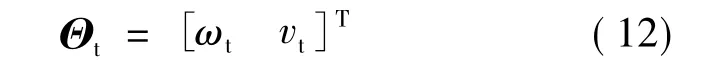
参数的误差:

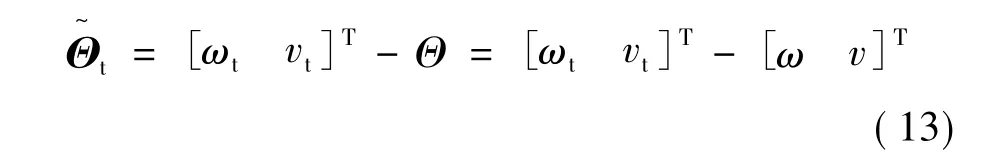
则式(11)可表示:

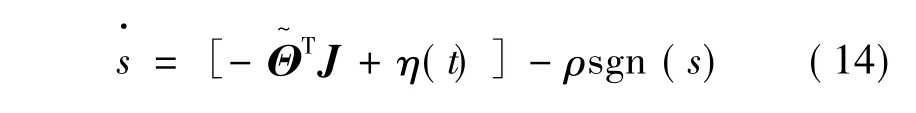
权值的调整可按下式进行:

选择切换增益ρ＞‖η(t)‖。

2．1．3 神经滑模控制器稳定性分析［5］

这里定义 Lyapunov 函数［5，7］:

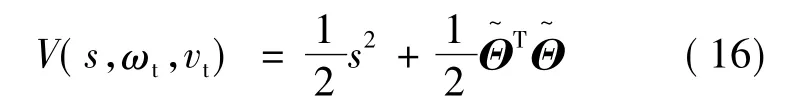
则

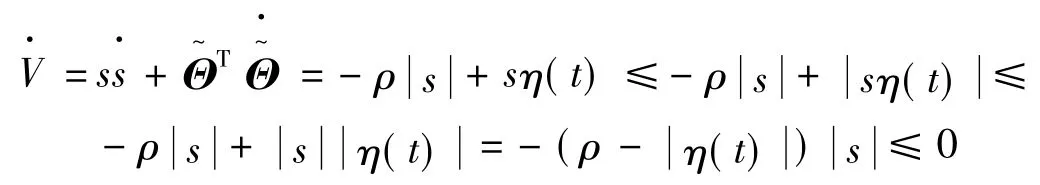
所以意味着切换函数s和参数误差Θt在平衡点s=0，ωt=ω，vt=v处是一致稳定的。因此，所设计的神经滑模控制器能够保证系统的稳定性。

3系统仿真与结果分析

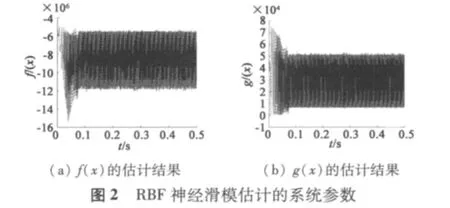
当参考速度为1 500 r/min时，取λ为88，采用结构为7-16-2结构的RBF神经网络对空载情况下电机的结构参数进行逼近，RBF神经网络逼近的系统参数如图2所示，根据式(5)计算出的结果与RBF逼近结果之间的误差如图3所示。从图上可以看出，估计误差精度是千分之几，说明估计的结果比较接近实际的参数值。

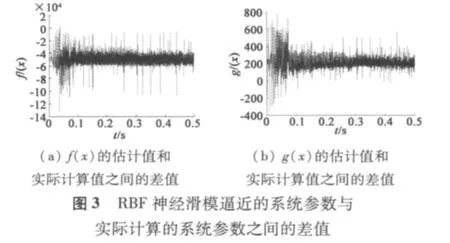
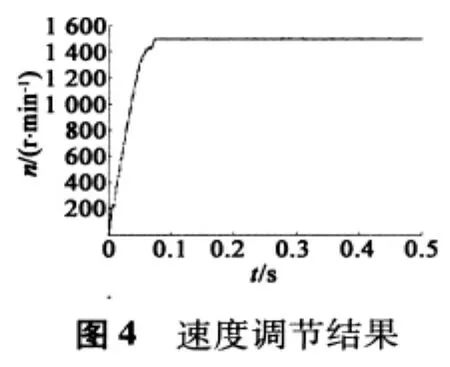
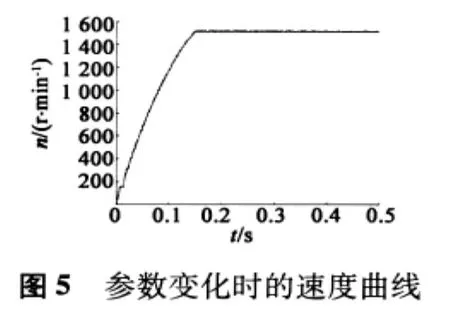
速度跟踪曲线如图4所示，为验证电机参数发生变化时的调速情况，对电机空载起动，给定的参考速度为1 500 r/min，假设增加电机的阻值和转动惯量，其它参数不变的情况进行了仿真。图5为电机参数发生变化时电机的速度曲线，从图5可以看出，由于转矩惯量增加，与图4相比，电机进入稳态的时间从约0．075 s增加到约0．15 s，稳态时最大的稳态误差为16．6 r/min。此结果说明调速系统在电机结构参数发生变化时仍具有较好的性能。

4结 语

本文对开关磁阻电动机调速系统的速度控制问题提出一种基于RBF神经网络的自适应滑模控制策略，通过神经网络的在线学习实时估计系统的结构参数，实现了基于反馈线性化的自适应滑模控制，仿真结果证明了所提出控制方法的有效性。

［1］ Haiqing Y，Panda S K，Chii L Y．Experimental Investigation of Feedback Linearization Controller for Switched Reluctance Motor［C］//IEEE Power Electronics Specialists Conf．1996，2:1804-1810．

［2］ Shi C，Cheok A D．Performance comparison of fused soft control/hard observer type controller with hard control/hard observer type controller for switched reluctance motors，Systems，Man，and Cybernetics［J］．Part C:Applications and Reviews，IEEE Transactions on，2002，32(2):99-112．

［3］ 韩顺杰，李慧，王玉华，等．开关磁阻电机滑模变结构控制器的设计［J］．吉林工学院学报(自然科学版)，2001，22(1):49-52．

［4］ Huang S J，Huang K S，Chiou K C．Development and application of a novel radial basis function sliding mode controller［J］．Mechatronics，2003，13(4):313-329．

［5］ 刘金琨．滑模变结构控制MATLAB仿真［M］．北京:清华大学出版社，2005．

［6］ Horng J．Neural adaptive tracking control of a DC Motor［J］．Information Sciences，1999，118(1-4):1-13．

［7］ 王晶．基于智能技术的非线性系统稳定自适应控制［D］．博士后研究工作报告，1999．