基于降阶扩展卡尔曼滤波的永磁同步电动机无传感器控制

李 宏，张 群，郑 勇

(西北工业大学，陕西西安710072)

0引 言

永磁同步电动机因具有转矩惯性比高、功率密度高、功率因数高、效率高等优点，得到了越来越广泛的应用。在永磁电机的调速系统中，关键要得到永磁转子的实时磁极位置。一般通过在电机转子上安装机械式传感器，如光电编码器或旋转变压器来测量转子的位置，并提取转子的速度信息［6］。然而传感器的存在增加了系统的成本，不仅带来机械安装精度等问题，而且使系统的可靠性降低，在实际应用中并不理想。因此无机械传感器的控制方法得到了越来越多的关注。

目前，永磁同步电动机的无速度传感器调速方法可以大致分为以下两类:

(1)在电机非线性模型上发展非线性方法和线性估算方法;

(2)在电机其它的特性上分析，如反电势法、电流谐波法和注入谐波法。扩展卡尔曼滤波(EKF)就是建立在电机非线性模型基础上的一种最优化非线性方法。该方法具有较强的抗噪声能力，然而EKF算法阶数高，对最小方差矩阵的繁重计算使之对处理芯片具有很高的要求，限制了其在实时控制系统中的应用。

本文提出了一种基于降阶扩展卡尔曼滤波器(REKF)来预估转子位置和速度的新算法，选取定子绕组在α、β轴的反电势eα、eβ和转速ω作为状态变量，阶数由4阶降为3阶，计算量明显减少，算法更加简单，在性能上则继承了传统EKF的优势。

1扩展卡尔曼滤波器原理

卡尔曼滤波算法是一种线性最优递推滤波算法，能够在有随机干扰和噪声的情况下，以线性最小方差估计给出状态变量的最优估计值。

永磁同步电动机在静止α-β坐标系下的数学模型［3，5］:

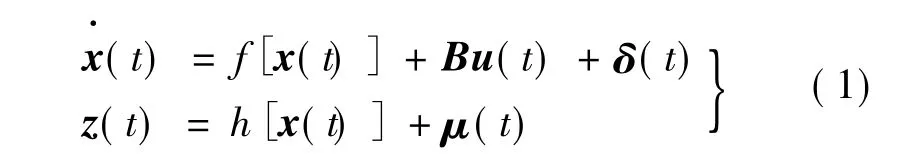
其中:

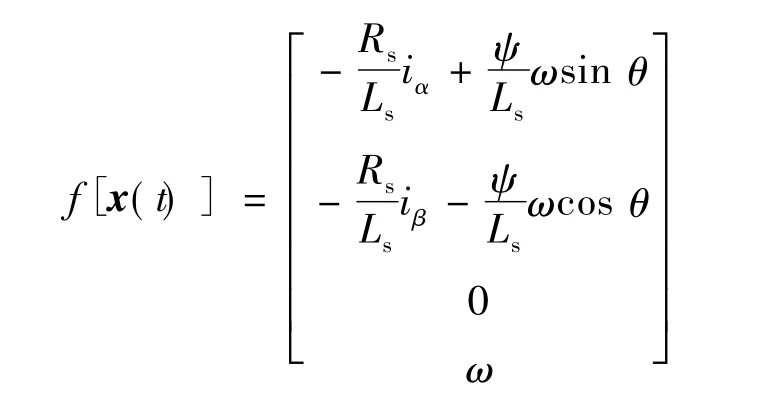
上述数学模型中，系统状态变量 x=［iαiβω θ］T，输入变量 u=［uαuβ］T，输出变量 z=［iαiβ］T，iα、iβ为 α、β 轴定子电流，Ls为相电感，Rs为相电阻，eα、eβ为定子绕组 α，β 轴反电势，Ψ为永磁体磁链，ω为转子角速度，θ为转子位置，δ(t)为系统过程噪声，μ(t)为系统测量噪声，δ(t)、μ(t)协方差阵分别为Q、R。

对 f［x(t)］、h［x(t)］进行线性化处理可得雅克比矩阵:

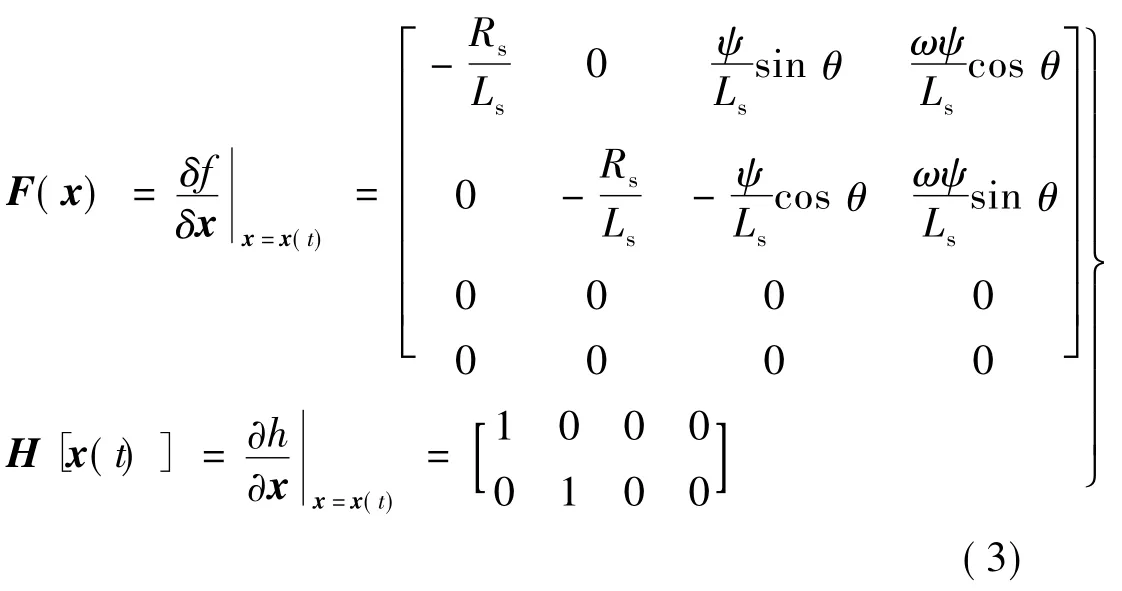
设Δx(t)足够小，得线性化方程:

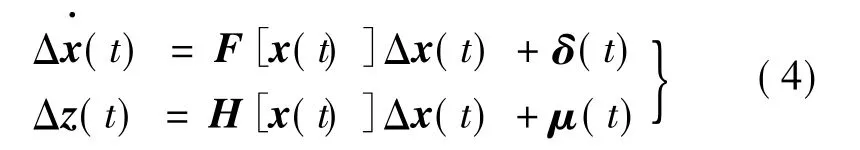
设采样周期为T，对式(4)进行离散化处理:

式中:Φ为状态转移矩阵，Φ(k)≈I+F(k)T。

于是得到下列5步卡尔曼滤波方程:

一步预测:

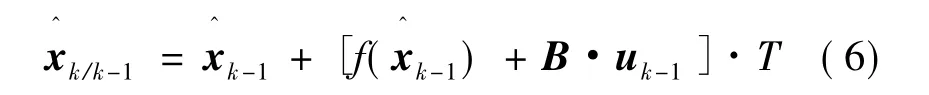
状态估计:

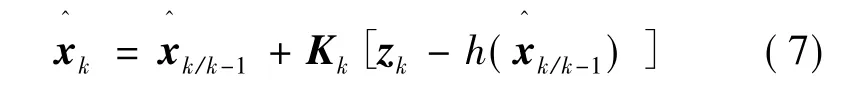
一步预测均方差:

估计均方差阵:

增益:

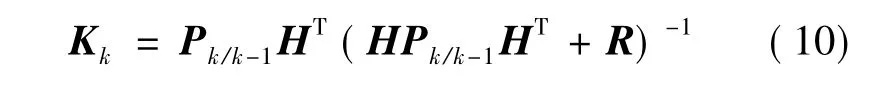
2降阶卡尔曼滤波器

扩展卡尔曼滤波器算法具有抑制噪声干扰，提高状态估计准确度的优点，但是其系统矩阵仍然是耦合的，且计算量较大，不利于实时性的运用。下面来讨论一种降阶卡尔曼滤波器，通过适当地选取状态变量，简化滤波器的结构，加快系统运行时间。

由永磁同步电动机数学模型可知，电机反电势:

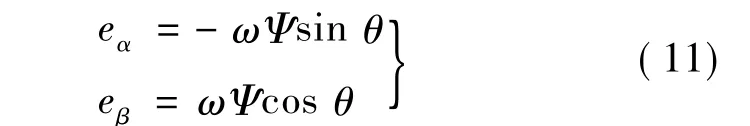
对 f［x(t)］、h［x(t)］进行线性化处理，可得雅克比矩阵:

设采样周期为T，对式(13)进行离散化:

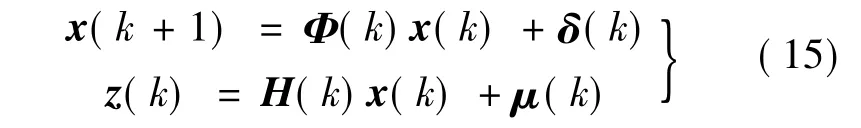
状态转移矩阵:

由式(11)可知，状态变量 eα、eβ包含着转子位置信息，因此只要得到 eα、eβ，即可解算出转子位置θ。然而按照EKF算法，这个系统是一个无输入信号的非线性系统，而且输出量包含eα和eβ并不能直接观测，需对式(1)进行适当处理。

由式(1)可得:

将式(17)近似离散化:

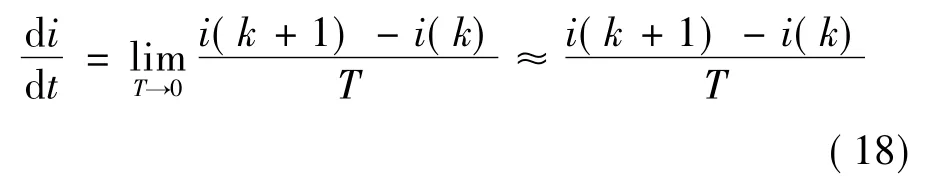
将式(18)代入式(17)，可得:

由此便可采用扩展卡尔曼方程进行状态估计了。此时的扩展卡尔曼滤波器经过了降阶处理，运算量大大降低。由于在估算过程中没有用到电机的永磁体磁链Ψ，鲁棒性更好。

与卡尔曼滤波式(1)～式(10)相比，降阶卡尔曼方程结构大大简化，在运算过程中占用更少的存储空间，更易于数字化实现。

3仿真模型的建立及结果分析

图1 无传感器永磁同步电动机调速系统仿真模型

为了验证这种基于降阶扩展卡尔曼滤波算法的永磁同步电动机无传感器控制的可行性和有效性，本文基于Matlab/Simulink平台，建立了基于降阶扩展卡尔曼滤波的永磁同步电动机无位置传感器控制系统的仿真模型，仿真模型如图1所示，永磁同步电动机采用id=0的矢量控制策略实现转速和电流的双闭环控制。电机参数如表1所示。

表1 仿真试验用电机参数

采样周期 T=1×10-6s，初始值取 x0=

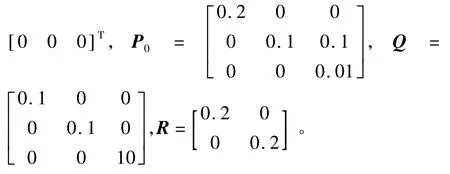
根据上述降阶扩展卡尔曼滤波算法，编写Matlab函数，估算出状态变量 eα、eβ、ω。转子位置 θ可由下式得到:

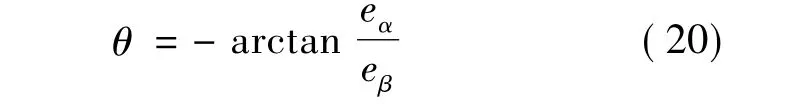
当给定转速nref=400 r/min时，空载起动，进入稳态后，在0．05 s时突加负载转矩Te=10 N·m。图2为降阶卡尔曼滤波器输出的反电势波形。

图3为降阶卡尔曼滤波器估计的转子转速与实际转速曲线。可以看出，采用降阶扩展卡尔曼滤波器估算的转子转速对于实际转速具有良好的跟踪性能，负载突变时，亦能较快地跟踪实际转速。图4给出了电机估计转速与实际转速之间的误差，由图可知，在电机高速运行时，转速误差很小，电机运行平稳。

图5为估计的转子位置曲线。仿真结果表明，降阶扩展卡尔曼滤波算法对永磁同步电动机的位置估算精度较高，在初始暂态过程之后，能够收敛到实际值，而且对负载转矩扰动的鲁棒性较强。

图2 估计的反电势波形

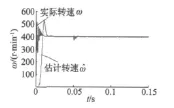
图3 估计的转速曲线

图4 估计的转子转速误差

图5 估计的转子位置曲线

4结 语

本文在分析了传统扩展卡尔曼滤波器原理的基础上，提出了一种基于降阶扩展卡尔曼滤波算法的永磁同步电动机无速度传感器控制方法，并通过Matlab/Simulink平台，建立了控制系统的仿真模型，仿真试验结果验证了算法的有效性。新算法不仅延续了传统扩展卡尔曼滤波算法的优势，而且算法更加简单，更易于数字化实现。

［1］ Kim Y H，Kook Y S．High Performance IPMSM Drives without Rotational Position Sensors Using Reduced-Order EKF［J］．IEEE Trans．on Energy Conversion，1999，14(4):868-873．

［2］ Wang W，Zhang M，Wu Q．Application of Reduced-Order extended Kalman Filter in permanent magnet synchronous motor sensorless regulating system［C］//International Conference on Digital Manufacturing and Automation．2010:271-274．

［3］ Zheng Z，Li Y，Fadel M．Sensorless Control of PMSM Based on Extended Kalman Filter［C］//European Conference on Power Electronics and Applications．2007:1-8．

［4］ 张敏．基于DSP的永磁同步电机无传感器控制系统的研究［D］．南京:南京航空航天大学，2009．

［5］ 吴永前，李玉忍．扩展Kalman滤波在永磁同步电机无速度传感器调速系统中的应用［J］．电气传动自动化，2001，23(6):3-6．

［6］ 阮毅，陈维钧．运动控制系统［M］．北京:清华大学出版社，2006:230-241．