考虑邻齿效应的直线旋转步进电动机推力计算

孙贤备，杨文焕

(上海理工大学，上海200093)

0引 言

双三相直线旋转步进电动机是在传统的旋转式步进电动机和圆筒式直线步进电动机的基础上进行创新设计的，既能旋转运动又能直线运动，满足了电机对多自由度运动的要求。

双三相直线旋转步进电动机直线段部分1个定子齿距等于2个转子齿距。文献［5］推导了直线旋转步进电动机的直线推力，但是并没有考虑邻齿的影响，与实际电机推力有很大差别。本文考虑邻齿效应，对电机的直线推力采用了分段计算的方法，推导出的直线推力更加符合实际电机推力。

1电机结构及工作原理

本文所介绍的双三相直线旋转步进电动机是磁阻式步进电动机，其定子由产生旋转力矩的定子段和产生直线推力的定子段构成。产生旋转力矩的电机由0．5mm厚的矽钢片叠在一起组成，叠片结构如图1所示。

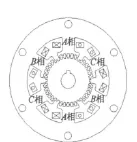
图1 产生旋转力矩部分电机叠片

图1中，电机定子共有3对极，转子共有40个小齿，三相绕组分别绕在电机的6个极靴上，有叉的表示电流流进纸面方向，圆圈表示电流从纸面向外流出。下面以三相单三拍通电方式说明其旋转原理:当只有A相绕组通电时，由于磁通具有沿最小路径闭合的特性，转子将收到磁阻转矩的作用，最终使A相的定子齿与转子齿完全正对。此时，B相定子齿与转子齿顺时针错开3°，C相定子齿与转子齿逆时针错开3°。当A相断电，B相通电时，在磁阻转矩的作用下，转子顺时针转过3°，使B相定子齿与转子齿完全正对。同理，B相断电，C相接通时，转子再顺时针转3°。只要按A→B→C→A……的顺序不断通电，转子就会沿顺时针一直转动。若按A→B→C→A……顺序通电时，则电机反向转动。

产生旋转运动的定子是传统的旋转式步进电动机的定子，比较常见。产生直线推力的定子是用特定的叠片错位法而形成的，三相绕组分别绕在电机定子的6个极靴上，绕组与旋转部分绕组相同。定子结构如图2所示。

图2 产生直线推力的定子

双三相直线旋转步进电动机的转子沿径向和轴向双向开槽，结构如图3所示。

转子在圆周方向上有齿槽分布，在径向上也有齿槽分布。产生直线推力的定子在轴向齿宽是定子轴向槽宽的1/2，直线部分定子在轴向的齿宽和转子在轴向的齿宽相等，转子在轴向的齿宽是转子轴向槽宽的2倍。以三相单三拍通电方式说明其直线运动原理。

如图4所示，当只有直线部分定子绕组A相通电时，由于磁通具有沿最小路径闭合的特性，转子将受到磁阻推力，最终使定子A相齿与转子齿完全正对，此时，B相定子齿正好与转子齿错开1/2个齿宽，而C相定子齿与转子齿反向错开1/2个齿宽。当A相断电，B相通电时，由于磁通具有沿最小路径闭合的特性，转子将受到向左的磁阻推力，使转子向左运动1/2个齿宽，定子B相齿与转子齿完全正对。同理，B相断电，C相通电时，转子再向左移动1/2个齿宽。只要按A→B→C→A……顺序通电时，转子将一直左移，每步走1/2个齿宽。若按A→C→B→A……顺序通电时，转子将反向运动，每步仍走1/2个齿宽。

图3 电机转子

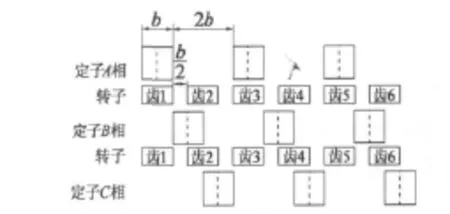
图4 电动机直线运动原理图

2直线推力计算

为了定量分析方便，作如下假设:(1)电机铁心磁导率为无穷大，即μFe=∞。(2)不计去磁端磁通。

步进电动机的推力曲线呈正弦，当定子齿与转子齿完全正对时，推力为零，当定子齿与转子齿半正对时，推力达到最大，此时电角度为90°，即1/4个周期。步进电动机的气隙比磁导为:

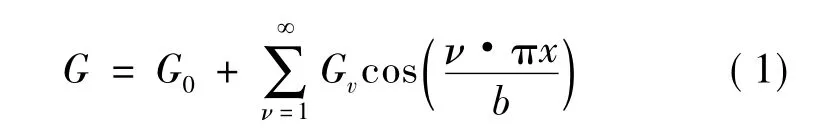
式中:G0为一个齿距内气隙比磁导的恒定分量，单位H/mm;Gν为一个齿距内气隙比磁导的ν次谐波分量幅值;b为转子齿宽，单位mm;%100%90;x为定转子齿中心线X向的偏移距离，单位mm。

仅考虑基波分量时，步进电动机的气隙比磁导:

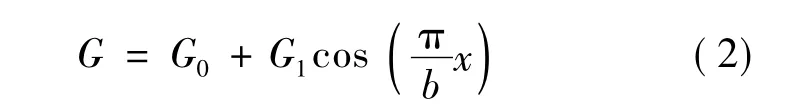
气隙磁导:

式中:zs为定子每极齿数;l为铁心每端叠厚。

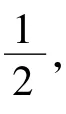
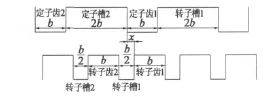
图5 -≤x≤时定转子位置

一个齿的气隙体积:

式中:g为气隙长度;b为齿宽。

因此，气隙磁能可表示:

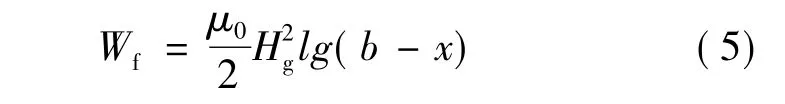
式中:Hg为气隙的磁场强度，A/mm。

当定子和转子发生相对运动，有微小位移dx时，则:

而

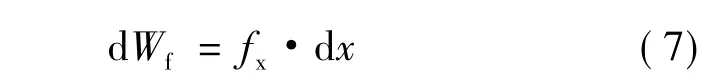
因此，电磁力:

而气隙磁势:

因此电磁力可表示为:

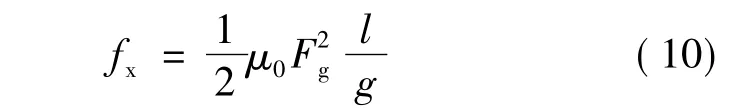
气隙磁导:

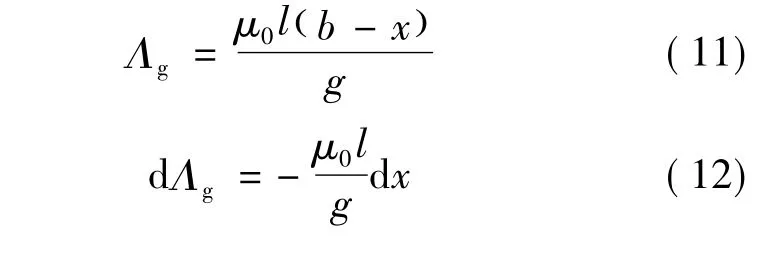
将式(12)代入式(10)，得到:

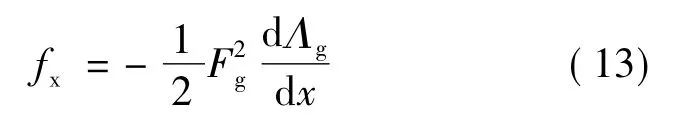
在假定定子铁心磁导率为无穷大和不计去磁端磁通的条件下，绕组电流产生的磁势全在气隙中，因此有:

式中:Fi为一相励磁磁势，Fi=NI，N为一相绕组匝数，I为一相励磁电流。

考虑到式(3)，可得到:

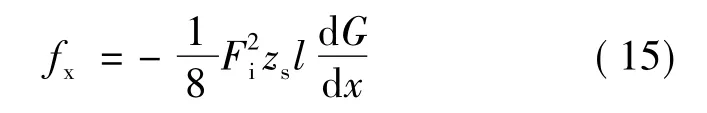
由式(2)求导后代入式(15)，可得:

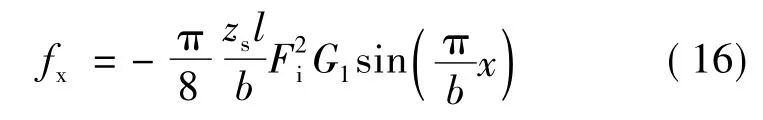
图6 ＜x＜b时定转子位置

此时要考虑到转子齿2和定子齿1之间的推力。转子受到的电磁力fx=f1-f2，其中f1为转子齿1与定子齿1之间的推力，f2为转子齿2与定子齿1之间的推力。假设产生转子齿1推力的磁势Fg1和产生转子齿2推力的磁势Fg2与定子齿槽的正对面积成正比，则:

由式(2)、式(3)和式(12)可推导出:

将式(17)、式(18)、式(19)代入式(10)，得到

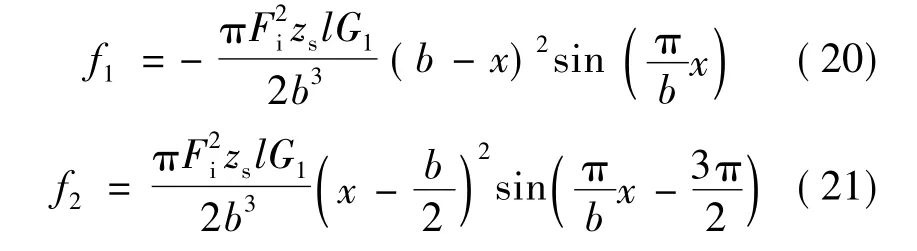
因此，电磁力:

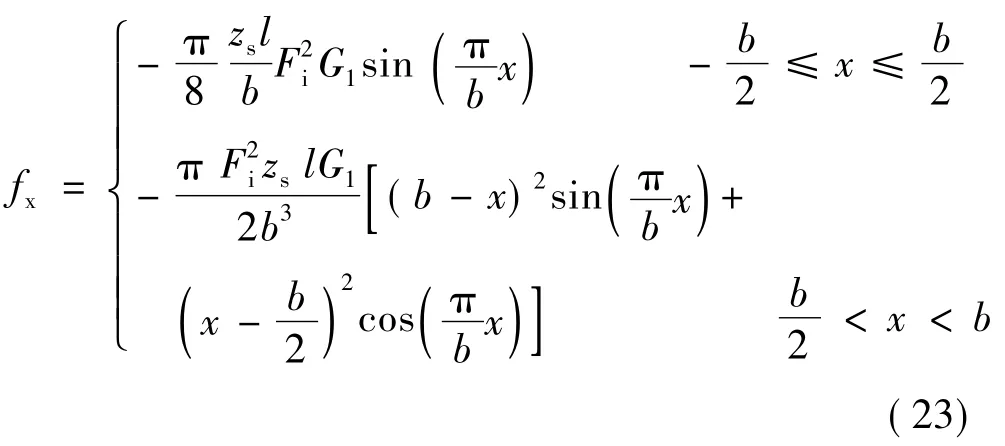
设定电机每相齿数zs为13，铁心每端叠厚l为1 m，励磁磁势为 60 A，G1为 0．575 ×10-5H/m，用以上参数计算得到fx的幅值为52．8 N。

3仿真分析

利用Ansoft有限元仿真软件，对双三相直线旋转步进电动机直线运动部分进行静态仿真，建立2D等效模型如图7所示。

图7 电机2D仿真模型

由于此电机结构的特殊性，建立起的2D等效仿真模型与直观有一定差别。电机参数设定为:每相齿数为13，定子齿宽2 mm，槽宽4 mm，转子齿宽2 mm，槽宽1 mm，气隙为0．3 mm，励磁电流为60 A，仿真得到的直线推力曲线如图8所示。

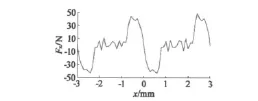
图8 Ansoft仿真直线推力曲线

由图8可知，直线推力曲线周期为3 mm，正好是转子一个齿距，呈分段形状，在正对位置-1≤x≤1 mm位置时，曲线呈幅值48 N的正弦形状，其余部分波动较大，这是邻齿效应的结果。仿真结果得出的推力幅值48 N和由推导出的公式计算得出的推力幅值52．8 N比较接近，证明理论推导公式的正确性。

由于公式推导时在转子齿2未与定子齿1正对时(图5)，忽略了他们之间的推力，而且假定铁心磁导率为无穷大，不计漏磁等，因而得到的推力曲线误差较大。用Anosft有限元软件仿真考虑到了未正对时的推力和漏磁等问题，因此得到的曲线与实际较为接近，有效地解决了理论公式计算的不足。

4结 语

双三相直线旋转步进电动机由于其结构的特殊性，产生直线推力部分定子1个齿距对应转子2个齿距，本文运用理论推导出其推力计算公式，得出其推力曲线是分段函数，并用Ansoft有限元软件进行仿真，验证了理论计算公式的正确性，为双三相直线旋转步进电动机的控制奠定了基础。

［1］ 丁志刚．直线步进电动机的原理控制和应用［M］．北京:机械工业出版社，1994．

［2］ 陈晓刚，赵荣详，黄进，等．凸极同步电机非均匀气隙磁导的计算［J］．电工技术学报，1998，13(1):15-17．

［3］ 葛宝明，赵楠．横向磁场直线开关磁阻电机及其控制系统［J］．中国电机工程学报，2007，27(33):22-29．

［4］ 于学海．横向磁场直线开关磁阻电机的研究［D］．北京交通大学硕士学位论文，2006:9-40．

［5］ 怡勇．磁阻式直线旋转电机设计及控制系统研究［D］．上海理工大学硕士学位论文，2009:10-20．

［6］ 严兰州．双径向直线旋转步进电机的研制［D］．上海理工大学硕士学位论文，2010:31-38．

［7］ ANSOFT Corporation．Getting Started with Maxwell:Transient Problem［M］．2005．

［8］ ANSOFT Corporation．Ansoft Maxwell Field Simulator V12-Training Manual［M］．2005．

［9］ Liu C T，Kuo J L．Experimental investigation and 3-D modelling of linear variable-reluctance machine with magnetic-flux decoupled windings［J］．IEEE Transactions on Magnetic，1994，30(6):4737-4739．

［10］ Takemoto M，Chiba A，Akagi H，et al．Radial force and torque of a bearingless switched reluctance motor operating in a region of magnectic saturation［J］．IEEE Transactions on Industry Applications，2004，40(1):103-112．

［11］ Ho E Y Y，Sen P C．Control dynamics of speed drive systems using sliding mode controllers with integral compensation［J］．IEEE Transactions on Industry Applications，1991，27(5):883-892．