基于RBF神经网络的SVPWM研究

宣光银，胡 丹，车 畅

(西华大学，四川成都610039)

0引 言

电压空间矢量脉宽调制(SVPWM)改进了脉宽调制(PWM)算法，视逆变器和电机为一体，通过跟踪圆形磁场来控制PWM电压，使电机的旋转磁场与电压空间矢量运动轨迹联系起来，从而明显减小逆变器输出电流的谐波成分，降低了电机的转矩脉动，提高了直流电压利用率，因此得到了广泛应用［1］。SVPWM算法通常采用查表法或者复杂的在线计算来实现三角函数的计算，这就要求器件有更多的资源来满足这一功能;同时，也限制了系统的灵活性和精度。而数据拟合优势突出的人工神经网络(ANN)为SVPWM的实现提供了新的途径［2-4］，文献［5-6］中采用BP神经网络实现空间矢量，文献［7］提出利用小波神经网络实现空间矢量脉宽调制，并与BP神经网络作了对比。这些网络因为隐节点数和隐层数不易确定，需要进行大量的训练和测试直到找到合适的隐节点数和隐层数，耗时费力;而且BP网络的权值调整采用的是梯度下降法，存在易陷入局部极小值和收敛速度缓慢的不足。

本文从SVPWM的基本原理出发，利用径向基网络(RBF)建立模型对开关函数进行离线训练后将其封装到Simulink环境中，并在异步电动机控制系统中对该网络进行了仿真研究，证明其有效性。

1电压空间矢量的调制

典型的三相逆变电路共有八种工作状态，其中有六个有效状态(u1～u6)和两个无效零状态(u7、u8)。此时，电机磁链轨迹如图1中的A～F正六边形所示。

为了获得圆形旋转磁场，一般利用六个非零的基本电压空间矢量进行线性组合得到更多的开关状态，这样就可以获得更多边数的正多边形去逼近圆形磁场轨迹［8］，如图2所示。

图1 正六边形磁链轨迹

图2 电压空间矢量的线性组合

其中，ux和ux+60代表六个有效状态中相邻的两个基本电压空间矢量;uout是输出的参考相电压矢量;Tpwm为载波周期;t2、t2是基本电压矢量在Tpwm内的作用时间;θ为参考电压与x轴的夹角。则由合成原理得:

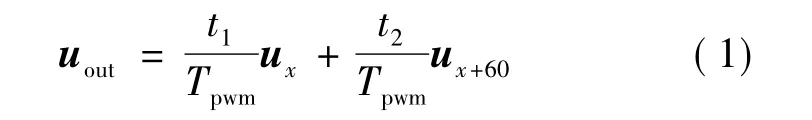
变换到直角坐标系d-q上来表示，得:

式中:M为调制信号与载波信号的幅值之比。求解上式得:

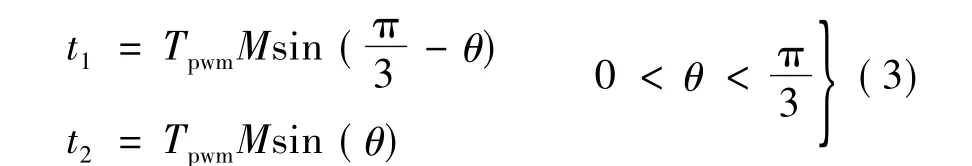
但Tpwm不一定恰好等于t1+t2，不足的时间就由零矢量所代表的状态来补充，用u0代表零矢量u7或u8，则u0作用的时间:

为了尽量减小输出谐波，常用七段对称分解法将所得的t1、t2、t0进行合成，有文献已经给出，当采用对称脉冲输出时谐波分量最小［9］。

欠调制时，旋转的参考电压相量总是处于正六边形最大内切圆内，如图1所示。在这一区域中，一个周期内产生三个连续的开关电压矢量，并由任意给定的参考电压矢量角度θ可得到各个扇区的开关矢量的占空比dA-ON、dB-ON、dC-ON，即可得到各个桥臂的开通和关断时间［10］:

各个扇区的开关导通时间占空比如下:

式中:m为调制因数;

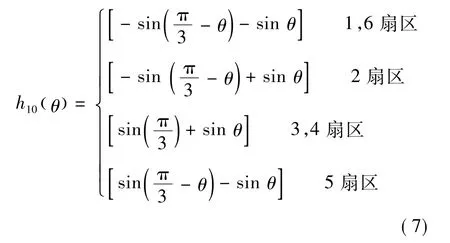
其它各扇区内的h20(θ)、h30(θ)表达式同样可得。通过 h10(θ)、h20(θ)、h30(θ)和 θ的关系建立训练样本训练RBF网络来实现对时间导通函数的逼近，样本的采样间隔为1°。

2基于RBF网络的SVPWM模型

2．1径向基神经网络

图3 RBF神经网络结构图

RBF(radialbasis function，RBF)神经网络一般为三层结构，如图3所示。图中的神经网络结构为 n-h-m，即网络有n个输入、h个隐节点、m个输出。其中，x=［x1，x2，…，xn］T∈Rn为网络输入矢量，ω∈Rh×m为输出权矩阵，b=［b1，b2，…，bm］T为输出单元偏移，y=［y1，y2，…，ym］T为网络输出，φi(·)为第i个隐节点的激活函数。RBF网络隐节点的基函数通常采用距离函数(如欧氏距离，即图中‖·‖)，并使用RBF(如高斯函数)作为激活函数，由此可得隐含层的第i个输出:

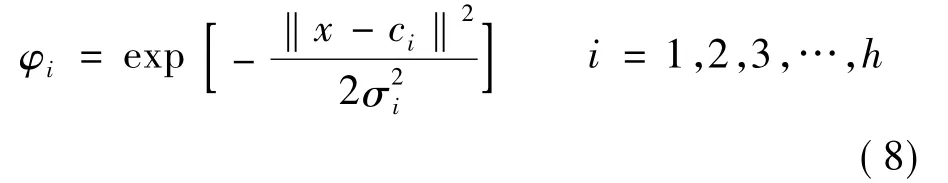
式中:ci为隐节点的中心矢量。输出层节点中的∑表示输出层神经元采用线性激活函数(也可采用其它非激活函数，如sigmoid函数)，则第j个输出可表示:

当RBF网络输入训练样本xp时，对应的期望输出dp就是教师信号，为了确定网络隐层到输出层之间的权值，需要将训练样本逐一输入，由式(9)可得出网络权值，从而实现对样本完全内插，即对所有样本误差为零;而对非训练集的输入，网络的输出值相当于对函数的内插，即实现对函数的逼近。

2．2 SVPWM的神经网络模型

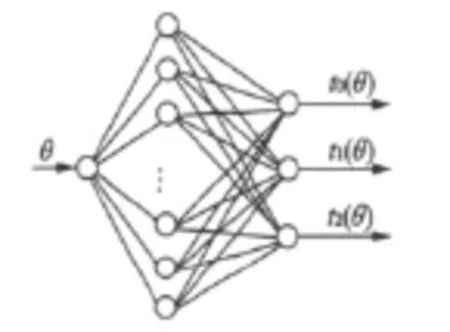
图4 RBF网络实现的时间计算模块

图5SVPWM生成模块

3仿真结果与分析

在Matlab中利用获得的训练样本对RBF网络进行训练并将其封装到Simulink中，同时建立异步电机控制系统对其进行仿真分析。

3．1时间导通函数的逼近

利用RBF神经网络BP网络逼近导通函数h10(θ)、h20(θ)、h30(θ)并采用均方误差(mse)作为训练的性能指标进行对比。均方误差的定义为:

其中，n=360;j为当前训练步数;ei为第i个样本的测试误差。

将采样得到的训练样本归一化，设定RBF网络的扩展常数spread=0．05，最大隐节点数为300;BP网络隐层节点数为20，最大步数为5 000，训练的目标精度为g=1×10-6。训练曲线和逼近曲线如图6～图7所示。

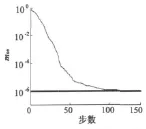
图6 RBF网络训练曲线

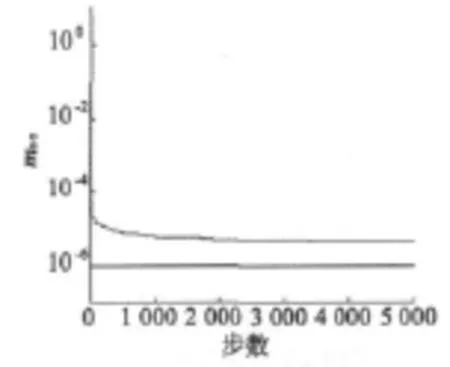
图7 BP网络训练曲线

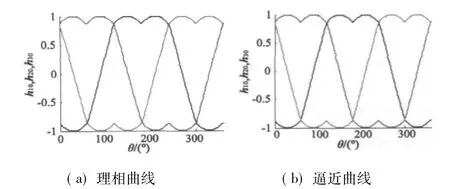
图8 RBF网络逼近的时间导通函数曲线

由图6～图7可以看出，随着训练的进行，RBF网络的均方误差不断减小，到140步时网络经过充分学习已完全满足目标要求;而BP网络在训练到指定上限步数时仍未达到目标精度，此外在500步以后BP网络的收敛速度非常缓慢。和BP网络相比，RBF网络训练时间大为减少，精度更高且不必关心隐节点数和层数的选取。用训练好的RBF网络逼近导通函数的曲线如图8所示，其中图8a为理论曲线，图8b为逼近曲线。可以看出，逼近曲线和理论曲线基本吻合，较好地逼近了导通函数。

3．2电机仿真波形

将训练好的RBF网络封装好后加入到异步电机控制系统，其中异步电机的参数为:P=4 kVA，UN=400 V，频率 f=50 Hz，Rs=1．405 Ω，Ls=0．005 8 H，Rr=1．395 Ω，Lr=0．005 9 H，互感 Lm=0．172 2 H，电机极对数 p=2，转动惯量 J=0．013 1 kg·m2，摩擦系数F=0．003 N·m·s;直流母线电压Udc=200 V，调制因数m=0．8。电机转速响应、电磁转矩和定子电流的波形如图9、图10所示。

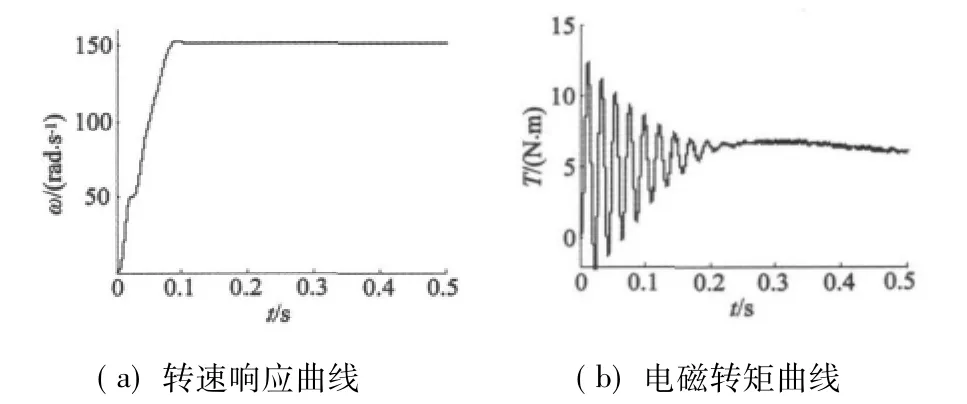
图9 转速响应及电磁转矩波形

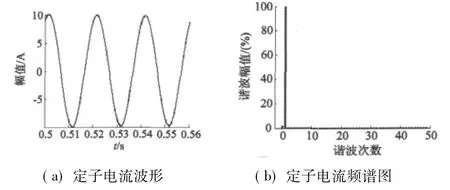
图10 定子电流及其频谱分析图

由图9的转速曲线和转矩曲线可以看出，转速在0．15 s之后基本恒定，电磁转矩在0～0．2 s内最大振幅不超过15 N·m，并于0．2 s后趋于稳定;图10中，定子输出电流近似为正弦波形，经频谱分析可知50次谐波含量在1%以内，谐波含量很小。该仿真结果表明，RBF-SVPWM在减小电流谐波降低转矩脉动等方面作用明显。

4结 语

本文利用RBF神经网络逼近导通函数，结果显示，RBF神经网络逼近速度快，精度高，同时由于RBF网络边训练边形成网络，训练简单可靠，无需人工调整网络结构再训练调试，大大节省了精力和时间。

将训练好的网络封装成Simulink模块后进行仿真，仿真结果表明，基于RBF-SVPWM的异步电动机控制系统响应快、输出的定子电流谐波小、转矩脉动低，证明了方案的可行性和有效性。由于训练简单，收敛速度快且效果明显，该算法易应用于实际。

［1］ 李永东．交流电机数字控制系统［M］．北京:机械工业出版社，2002:139-140．

［2］ Lee D C，Lee G M．A Novel Over Modulation Technique for Space-Vector PWM Inverters［J］．IEEE Trans．on Power Electron，1997:1014-1019．

［3］ Pinto J O P，Bose Bimal K，da Silva L E B，et al．A Neural-Network-Based Space-Vector PWM Controller for Voltage-Fed Inverter Induction Motor Drive［J］．IEEE Trans．on Industry Applications，2000，36(6):1628-1636．

［4］ Mondal S K，Pinto J O P，Bose B K．A Neural-Network Based Space-Vector PWM Controller for a Three-Level Voltage-fed Inverter Induction Motor Drive ［J］．IEEE Trans．ind Applicat，2002，38(3):660-669．

［5］ Hao P，Yuan J L，Zhong L．Probing Modification of BP Neural Network Iearning-Rate［C］//IEEE Proceeding of the International Conference on Machine Iearning and Cybernetics．Beijing，2002，11(4-5):307-309．

［6］ 杨新华，王关平，侯竑．基于人工神经网络的空间矢量脉宽调制实现研究［J］．电机与控制应用，2006，33(9):18-20．

［7］ 蔡宝平，刘永红，于丽丽，等．基于小波神经网络的SVPWM算法研究［J］．微特电机，2009(9):1-3．

［8］ Holtz J，Lotzkat W，Khambadkone M．On Continuous Control of PWM Inverters in The Over Modulation Range Including The Six-Step Mode［J］．IEEE Trans．Power Eleetron，l993(8):546-553．

［9］ 梅丛立，刘国海，廖志凌．空间矢量PWM谐波分析及其对电机转矩的影响［J］．微特电机，2004(7):16-19．

［10］ 元志．基于神经网络的逆变器的研究［D］．天津:天津理工大学，2007:28-30．