立式浮顶储罐基础隔震地震响应研究
2011-07-18孙建刚崔利富杜蓬娟赵长军
孙建刚,崔利富,杜蓬娟,赵长军
(1.大连民族学院土木建筑工程学院,116600辽宁大连,sjg728@163.com;2.东北石油大学土木建筑工程学院,163318黑龙江大庆;3.大连海事大学道路与桥梁工程研究所,116026辽宁大连)
立式浮顶储罐基础隔震地震响应研究
孙建刚1,2,崔利富3,杜蓬娟1,赵长军2
(1.大连民族学院土木建筑工程学院,116600辽宁大连,sjg728@163.com;2.东北石油大学土木建筑工程学院,163318黑龙江大庆;3.大连海事大学道路与桥梁工程研究所,116026辽宁大连)
为研究浮顶储罐基础隔震地震响应问题,将浮顶假定为均质刚性圆板,波高振动形式受浮顶约束假设为沿半径线性分布.由速度势理论出发,建立液体运动势函数、基底剪力、倾覆力矩表达,由板振动理论建立浮顶运动方程,由能量原理建立罐体运动控制方程.采用时程分析方法研究了浮顶储罐基础隔震的地震响应,数值结果表明:隔震基频宜取2~3 rad/s、隔震阻尼比宜取0. 1,Ⅰ类、Ⅱ类场地减震率效果好于Ⅲ类、Ⅳ类场地,场地不同对波高的影响不同,高径比对隔震浮顶储罐的地震响应影响不大.
浮顶储罐;基础隔震;波高;基底剪力;倾覆力矩
引发立式浮顶的震害主要包括浮顶的卡顶、失稳、罐壁象足屈曲、菱形屈曲、连接部件的破坏等因素[1-4].从储罐抗震问题研究角度看,侧重自由表面晃动的储罐地震响应分析文献多,考虑浮顶影响的文献相对较少[5-8].关于基础隔震研究,文献[9 -11]针对自由面储罐橡胶隔震已做了大量理论和实验研究,国外 Chalhoub and Kelly[12]、Malhotia[13]、Kim and Lee[14]、Shrimali and Jangid[15]等研究了自由面储罐滑移、橡胶垫隔震的问题,结果表明隔震能够有效降低储罐的倾覆力矩,减少罐壁的轴向应力,但对波高有放大效应.可见,储罐结构控制的研究多以自由面来考虑问题.实际的结构体系中,浮顶作为附加质量对储罐的晃动是有影响的.同时,由于地震激励产生晃动对浮顶的冲击作用也是浮顶设计的重要依据.鉴于此,本文考虑浮顶对动响应的影响,假定其为均质刚性圆板,波高振动形式假设为沿半径线性分布,研究基础隔震立式浮顶储罐地震响应的分析理论.
1 基本理论
1.1 基本假定
浮顶储罐内液体为无旋、无粘、不可压缩的理想流体,浮顶为均质刚性圆板,质量为m,储罐基础为橡胶隔震层,隔震层顶部位移为x0(t),隔震层为线性隔震,刚度为k0,阻尼系数为c0,储罐壳壁为弹性,具有位移 w(θ,z,t)的变化,地面输入激励为¨xg(t).罐几何和坐标系统见图1.

图1 罐几何和坐标系统
1.2 贮存液体圆柱壳的运动势及压力
液体产生的速度势由水平地震激励、液体的晃动、液体沿罐壁的径向运动构成.为此,将液体的速度势分解为由地面水平地震激励和隔震层运动产生的运动速度势φ1,浮顶晃动的速度势φ2,弹性壁径向运动产生的速度势φ3,则总的速度势为
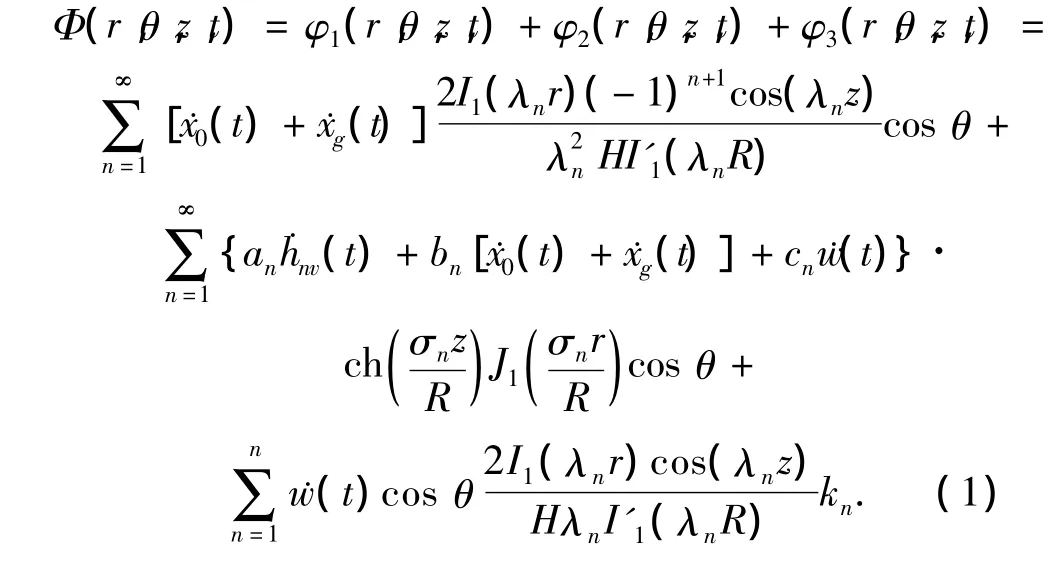
2 运动分析方程
2.1 浮顶运动方程
针对图1的基础隔震体系,由速度势Φ在浮顶产生的动水压力进行积分,推导得其运动方程为

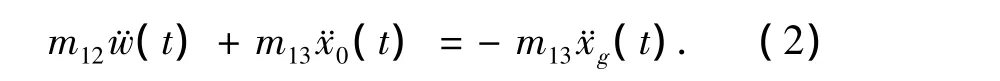
2.2 液体与壳体耦合振动方程

2.3 基础隔震层振动方程
由底层基底剪力在虚位移δx0上所做虚功等于隔震层的变形能和阻尼耗散所做的虚功得

2.4 系统振动方程
由式(2),(3)和(4)构成系统分析的振动方程,并考虑液体的晃动阻尼cL和壳体的阻尼cs,得

3 倾覆力矩和波高
侧壁倾覆力矩

4 数值分析
以15万方立式钢制浮顶储罐为研究对象,研究隔震与非隔震在地震动作用下,高径比、隔震基频、阻尼比、场地对地震响应的影响.
4.1 高径比对储罐地震响应影响
图2给出的是在El-Centro波地震作用下,加速度峰值为0.4g,隔震基频为2.093rad/s,隔震阻尼比为0. 1,高径比变化对隔震、非隔震储罐地震响应的影响对比曲线.

图2 不同高径比非隔震与隔震地震响应对比
图2为隔震、非隔震考虑浮顶和未考虑浮顶4种状态在不同高径比下的地震响应.从图中的结果分析可知:①高径比对非隔震储罐的倾覆力矩影响比较大,考虑浮顶储罐的侧壁倾覆力矩在高径比小于1的范围内,比自由表面储罐的小,并随高径比的增加而增大,底板产生的倾覆力矩是小项,且随高径比的增大变化不大;②隔震对考虑浮顶和未考虑浮顶相对于非隔震而言均有减震效应,两者的侧壁倾覆力矩、底板倾覆力矩的响应接近,且随高径比的增大,变化不大;③高径比对考虑浮顶和未考虑浮顶的非隔震储罐的波高有影响,浮顶具有降低波高的作用;④ 考虑浮顶和未考虑浮顶的隔震储罐的波高随高径比增大而降低,两者的波高差值不大.从图2(d)沿半径的时程曲线分析可见,隔震对自由表面波高有降低效应,对有浮顶的晃动波高有轻微的放大效应.
4.2 隔震基频对浮顶储罐地震响应影响
图3给出的是在El-Centro波地震作用下,其加速度峰值为0.4 g,隔震阻尼比为0. 1,不同隔震基频,5种高径比情况下的浮顶储罐倾覆力矩、晃动波高随隔震基频变化的关系曲线.
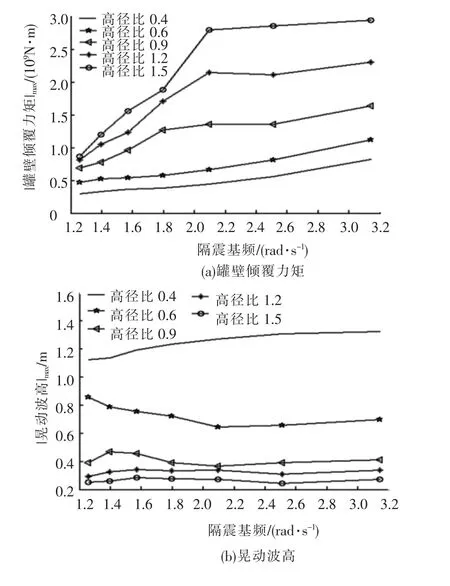
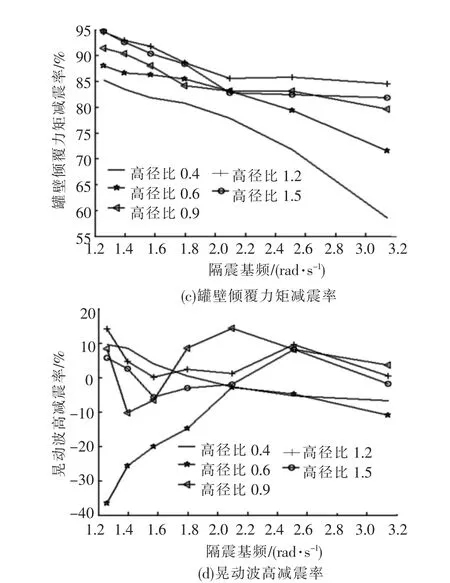
图3 储罐随隔震基频变化的地震响应分析
从图3(a)~(b)给出的结果分析可知倾覆力矩随隔震基频增大而增大,高径比对基底剪力、倾覆力矩有影响,在隔震基频一定时,基底剪力和罐壁的倾覆力矩随高径比增大而增大;总的倾覆力矩在高径比为0.4、0.6时,由于底板倾覆力矩的加入,在隔震基频大于2 rad/s时有些变化,但总的趋势为随隔震基频增大而增大;浮顶储罐的最大晃动波高随隔震基频变化不明显,高径比小晃动波高大.从图3(c)~(d)给出的减震率结果分析可知:① 隔震基频在1.2~3.2 rad/s之间,基底剪力和总的倾覆力矩的减震率达60%以上,且随着隔震基频的减小而减震效果增大,高罐减震效果大于矮罐;②隔震基频对波高的减震效果影响较大,隔震基频较小时对波高有放大效应,高径比不同放大效应不同,放大影响的隔震基频段也不同,隔震基频对高径比为0.4储罐的波高影响最大,而这一高径比恰为工程中常用的比值,由此可见在设计隔震时要结合储罐的投资造价及地震响应进行优化设计.
4.3 场地对隔震浮顶储罐地震响应影响
图4给出的是在4类地震波作用下,其加速度峰值为0.4 g、隔震阻尼比为0.1、隔震基频为2.093 rad/s、高径比为0.4的浮顶储罐倾覆力矩、晃动波高随时间变化的曲线.
图4的结果表明:场地不同,总倾覆力矩、晃动波高的反应时程不同.Ⅲ类、Ⅳ类反应峰值较大.其总倾覆力矩减震效果也有一定的差异,Ⅰ类、Ⅱ类场地的总倾覆力矩的减震率达90%以上,波高减震率达8%以上.Ⅲ类、Ⅳ类场地的总倾覆力矩的减震率达60%以上,Ⅲ类场地的波高略有放大,放大2.7%左右,Ⅳ类场地的波高减震率为14.4%,这一点说明隔震对不同的地震动的波高影响是不一样的,设计时要进行相应的时程分析来保证.

图4 不同场地隔震储罐地震响应时程
4.4 隔震阻尼比对隔震储罐地震响应影响

图5 隔震阻尼比对隔震储罐地震响应影响
图5给出的是在El-Centro波地震作用下,其加速度峰值为0.4 g、隔震基频为2.093 rad/s、高径比为0.4的浮顶储罐总倾覆力矩、晃动波高随阻尼比变化的曲线.
图5的结果表明:隔震阻尼比在0.05~0.15段考虑浮顶和未考虑浮顶储罐总的倾覆力矩随隔震阻尼比增大而下降,当隔震阻尼比大于0.15时,考虑浮顶和未考虑浮顶储罐总的倾覆力矩随隔震阻尼比增大而增大;隔震阻尼比在0.05~0.10段考虑浮顶和未考虑浮顶储罐的波高随隔震阻尼比增大而下降,当隔震阻尼比大于0.10时,考虑浮顶储罐的波高随隔震阻尼比增大而下降,未考虑浮顶储罐的波高随隔震阻尼比增大而增大.由此分析可知,隔震阻尼比存在优化区间,一般宜取0.1.
5 结论
1)由速度势理论出发,建立了考虑浮顶隔震储罐的基本理论,给出了基底剪力、波高、倾覆力矩的基本表达,并由能量原理建立了运动分析方程.
2)不隔震浮顶具有降低波高的作用,隔震对浮顶储罐和自由表面储罐的倾覆力矩均有良好的降低作用,隔震对非浮顶储罐波高有降低作用,但对浮顶储罐波高的降低效应取决于高径比、隔震基频及场地地震动特性等.
3)高径比影响浮顶储罐的地震响应结果.隔震储罐倾覆力矩受高径比的影响效果不大;波高随高径比增大而降低,隔震对自由表面波高有降低效应,对有浮顶的晃动波高有轻微的放大效应.
4)隔震基频在1.2~3.2 rad/s,且随着隔震基频的减小减震效果增大,高罐减震效果大于矮罐;隔震基频对波高的减震效果影响较大,隔震基频较小时对波高有放大效应,高径比不同放大效应不同,放大影响的隔震基频段也不同,存在优化区间,隔震基频宜取2~3 rad/s.
5)Ⅰ类、Ⅱ类场地减震率效果好于Ⅲ类、Ⅳ类场地,场地不同对波高的影响不同.隔震阻尼比宜取0.1.
[1] BERAHMAN F,BEHNAMFAR F.Seismic fragility curves for un-anchored on-grade steel storage tanks:bayesian approach [J].Journal of Earthquake Engineering, 2007,11:166-192.
[2]HAMDAN F H.Seismic behaviour of cylindrical steel liquid storage tanks[J].Journal of Constructional Steel Research, 2000,53:307 -333.
[3]NIWA A,CLOUGH R W.Buckling of cylindrical liquid- storage tanks under earthquake loading[J].Earthquake Engineering and Structure Dynamic, 1982,10:107-122.
[4]RAMMERSTORFER F G,SCHARF K,FISH F D.Storage tanks under earthquake loading[J].ASME Applied Mechanics Review, 1990,43(11):261 -282.
[5]NAKAGAWA K.On the vibration of an elevated water Tank II[R].Osaka:Osaka University,1955:317 -336.
[6]YAMAMOTO Y.The liquid sloshing and the impulsive pressures of oil storage tanks due to earthquakes[J].Journal of High Pressure Institute of Japan, 1965,3(1):2-8.
[7]MATSUI T.Sloshing in a cylindrical liquid storage tank with a single-deck type floating roof under seismic excitation[J].Journal of Pressure Vessel Technology, 2009,131/021303-1-021303-10.
[8]MATSUI T,UEMATSU Y,KONDO K.Wind effects on dynamic response of a floating roof in a cylindrical liquid storage tank[J].Journal of Pressure Vessel Technology, 2009,131/031307 -1 -031307 -10.
[9]孙建刚.立式储罐地震响应控制研究[D].哈尔滨:中国地震局工程力学研究所,2002.
[10]孙建刚,郝进峰,王振.储罐基底隔震振型分解反应谱计算分析研究[J].哈尔滨工业大学学报, 2005,37(6):649-651.
[11]孙建刚,王向楠,张荣花,等.立式储罐并联隔震地震反应分析[J].哈尔滨工业大学学报, 2009,41(10):105-109.
[12]CHALHOUB M S,KELLY J M.Shake table test of cylindrical water tank in base isolated structures[J].Journal of Structural Engineering,ASCE, 1990,116(7):1451-1472.
[13]MALHOTRA P K.New method for seismic base isolation of liquid storage tanks[J].Earthquake Engineering and Structural Dynamics, 1997,26:839 -847.
[14]KIM N S,LEE D G.Pseudo-dynamic test for evaluation of seismic performance of base isolated liquid storage tanks[J].Engineering Strcuctures, 1995,17(3):198-208.
[15]SHRIMALI M K,JANGID R S.Seismic response of liquid storage tanks isolated by sliding bearings[J].Engineering Structure, 2002,24(7):907-919.
Study on the seismic responses of vertical floating roof storage tanks with the base isolation
SUN Jian-gang1,2,CUI Li-fu3,DU Peng-juan1,ZHAO Chang-jun2
(1.College of Civil and Architecture Engineering,Dalian Nationalities University,116600 Dalian,Liaoning,China,sjg728@163.com;2.College of Civil and Architecture Engineering,Northeast Petroleum University,163318 Daqing,Heilongjiang,China;3.Institute of Road and Bridge Engineering,Dalian Maritime University,116026 Dalian,Liaoning,China)
To study the seismic response of floating roof storage tank with the base isolation,the floating roof is assumed as a homogeneous rigid circular plate,the vibration form of wave height is assumed as linear distribution along the radius.By the velocity potential theory,the velocity potential function of the liquid movement and the expression of base shear and overturning moment are established and by the plate vibration theory and energy principle,the motion equation for the floating roof and the motion equation for the tank system are presented,respectively.With the time history analysis,the seismic responses for the isolated floating roof storage tanks are studied.The numerical results show that the fundamental frequency of isolation is applicable to be 2-3 rad/s,while the damping ratio of isolation is 0.1.The damping rates ofⅠ,Ⅱ site are better than those ofⅢ,Ⅳ site.The effects of different sites on wave height are different,and the ratio of height to diameter has little effect on the seismic response of the isolated floating roof storage tanks.
floating roof storage tank;base isolation;wave height;base shear;overturning moment
P315.952
A
0367-6234(2011)08-0140-05
2010-03-16.
国家自然科学基金资助项目(51078063/E0808);教育部财政资助自主科研项目.
孙建刚(1959—),男,教授,博士生导师.
(编辑 刘 彤)
