基于巨磁阻抗效应磁场测量传感器研究

解伟男，梁慧敏

(1．哈尔滨工业大学 空间控制与惯性技术研究中心，150080哈尔滨，xieweinan@hit．edu．cn;2．哈尔滨工业大学电气工程及自动化学院，150001哈尔滨)

基于巨磁阻抗效应磁场测量传感器研究

解伟男1，梁慧敏2

(1．哈尔滨工业大学 空间控制与惯性技术研究中心，150080哈尔滨，xieweinan@hit．edu．cn;2．哈尔滨工业大学电气工程及自动化学院，150001哈尔滨)

针对非晶材料巨磁阻抗效应，设计并实现了一种新型磁场测量传感器，根据非晶丝的双峰特性，分析传感器的工作原理，设计传感器的闭环负反馈结构，建立了传感器的数学模型．在此基础上，通过分析传感器的误差传递函数，提出一种比例积分控制规律，可有效地消除传感器的稳态误差，提高传感器的线性度．实验结果表明:在该控制器的作用下，传感器的线性度优于0.2%，灵敏度达到1.759 V/Oe，所设计的传感器具有较好的性能指标．

磁传感器;巨磁阻抗效应;非晶丝

高性能的磁场测量要求传感器具有更小的体积，更高的灵敏度，更快的响应速度以及更好的稳定性．而传统的磁传感器，如磁通门传感器、霍尔元件、磁敏电阻、巨磁电阻等都不能很好地满足上述要求，1992年日本名古屋大学的Mohri教授等人发现当具有零或负磁致伸缩系数的CoFeSiB非晶丝通入高频电流时，非晶丝两端感生的电压幅值随外磁场而发生非常灵敏的变化，并把此现象称为“巨磁阻抗效应(Magnet-inductive effect)”［1］．巨磁阻抗效应在室温下对弱磁场非常敏感，而且效应显著、响应速度快，巨磁阻抗效应的研究［2－6］以及基于巨磁阻抗效应传感器的研制［7－12］都已经成为该领域的研究前沿．本文在前人研究的基础上，设计了基于巨磁阻抗效应磁场传感器的闭环负反馈结构，为传感器建立了数学模型，提出了比例积分的控制方法．实验数据表明，研制的传感器具有较高的灵敏度和线性度．

1 巨磁阻抗效应

巨磁阻抗效应是指非晶态合金材料的交流阻抗随外加磁场的改变而显著变化的效应，产生巨磁阻抗效应的本质是高频电流的趋肤效应［11］．

当交变电流I=I0exp(－iωt)流过非晶丝时，非晶丝两端的交流电阻抗表示为

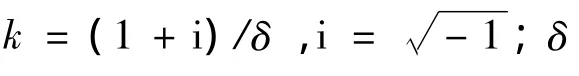
在强趋肤效应的作用下，非晶丝的电阻抗可以进一步近似表示为

非晶材料的电阻抗Z与激励电流角频率ω以及圆周磁导率μφ有关．在铁磁材料中，材料的磁导率与激励电流角频率ω及外加磁场Hex有关，这从而也说明了巨磁阻抗(GMI)效应．但铁磁材料的磁导率μ与外磁场Hex的具体函数关系，目前还没有完整的理论．

巨磁阻抗效应采用电阻抗的变化率来表征其大小，一般有2种定义:

式中:Z(Hex)为非晶材料在外加磁场下的电阻抗，Z(H0)为非晶材料在外加磁场为零时的电阻抗，Z(Hmax)为非晶材料在外加磁场达到饱和时的电阻抗．虽然这2种定义所表达的GMI(Z)大小不相同，但物理内涵是一样的．

2 传感器的设计与建模

众所周知，非晶材料具有圆周向各向异性时，其GMI效应随外加磁场变化将呈现双峰行为．图1给出了长为12 mm，直径为30 μm的钴基非晶丝的GMI效应曲线．图中采用式(3)来计算巨磁阻抗效应．根据非晶丝的特性，设计如图2所示的传感器结构．信号发生电路产生高频交变电流信号对非晶丝进行激励，当作用在非晶丝上的外加磁场发生变化时，非晶丝电阻抗产生变化，从而非晶丝两端电压也随之改变．电压信号通过峰值检波处理电路检测出其峰值大小，再经过低通滤波电路实现平滑处理，从而得到随外加磁场变化的电压信号．该电压信号与基准电压进行差分运算，运算结果通过设计的控制器后作用在反馈线圈中，产生反馈磁场，与外部磁场相抵消，从而构成负反馈回路．

图1 非晶丝GMI效应与外加磁场的关系

图2 传感器结构原理图

考虑到非晶丝GMI效应对磁场的特性，如图1所示，其对外加磁场最敏感、变化曲线相对线性的工作段不在零磁场附近，因此在非晶丝轴向方向通过偏置线圈施加偏置磁场Hb，使非晶丝工作在最佳区域．该系统的输入为被测磁场Hex，系统的输出为反馈线圈中的电流，其与反馈磁场Hf成正比．滤波电路选用二阶滤波器，滤波器的传递函数为

其中:T1和T2分别为滤波器设计的时间常数，而非晶丝对外加磁场响应的时间常数远远小于T1和T2，因此由施加在非晶丝的外部总磁场He到滤波器输出电压U1的传递函数可以简化为

其中:K为该环节的静态放大倍数．

差分电路的输入与输出关系为

其中:Ub(s)为偏置电压．

令控制器的传递函数为P(s)，则控制器的输入输出关系为

假设控制器的输出电压为U3(t)，反馈线圈中的电流为If(t)，根据法拉利电磁感应定律得

其中:R为反馈线圈回路总的直流电阻，Φs(t)为反馈线圈中的总磁通，即被测磁场产生的磁通Φex(t)、反馈线圈产生的磁通Φf(t)以及偏置线圈产生的磁通Φb三者的矢量和．

反馈线圈采用细长螺线管．被检测磁场在反馈线圈中形成的磁通大小为

其中:μ0为真空磁导率，n为螺线管单位长度的匝数，l为螺线管的有效长度，S为螺线管的有效面积．

同理，反馈磁场在反馈线圈中形成的磁通为

根据传感器的设计要求，偏置线圈中的电流保持不变，即偏置磁场在反馈线圈中产生的磁通是常值．考虑到各个磁场作用的方向，式(9)可以变换为

其中:V=lS为螺线管的有效体积．

将式(12)进行拉普拉斯变换，可得

考虑到反馈线圈为细长螺线管，则反馈线圈中的电流与反馈磁场之间的关系为

非晶丝所承受的总磁场为

由于反馈线圈中的电流与反馈磁场成正比，因此为方便测量，以反馈线圈中的电流为输出．利用式(6)～(8)、(13)～(15)可绘出传感器的动态方框图如图3所示．

图3 传感器的动态方框图

根据传感器的设计，使偏置电压Ub抵消偏置磁场对非晶丝的作用，则传感器的动态方框图可以简化为图4．根据图4可以得到系统的传递函数为

其中:P(s)为系统所需要设计的控制器．

3 控制器设计及实验结果

图4所示的传感器控制系统误差为期望输出与实际输出之差．根据系统的传递函数，可得传感器的误差函数

图4 传感器简化动态方框图

传统的基于非晶材料巨磁阻抗效应磁场测量传感器中，控制器仅仅采用比例环节．在系统为常值输入，即Hex(t)=1(t)时，假设比例环节的系数为KP，此时，应用拉氏变换的终值定理可得传感器的误差为

可见，传统的传感器在常值输入时存在稳态误差，即负反馈线圈产生的磁场Hf不能完全抵消被测磁场Hex．这意味着，非晶丝在稳态时，不能工作在一个固定的工作点，而是工作在一个固定的区域．而非晶材料GMI效应曲线的非线性导致不同工作点的GMI效应不同，对传感器来说，也就是在不同工作点上，传感器传递函数中的系数K不同，从而导致不同工作点上的稳态误差不同．因此，对测量数据进行拟合后得到的结果其线性度较差．本文设计的传感器采用PI控制器，即令控制器的形式为

在常值输入Hex(t)=1(t)时，应用拉氏变换的终值定理可得传感器的误差为

所以，传感器在常值输入时的稳态误差为零，即反馈线圈产生的磁场Hf与被检测磁场Hex大小相等，方向相反．这意味着，非晶丝在稳态时，一直处于预先设计好的工作点，因此，对测量数据进行拟合后得到的结果其线性度较高．

根据上述原理设计传感器，采用PI控制器，供电电压为±5 V，激励信号频率为10 MHz，反馈线圈单位长度的匝数为n=4 500匝/m，在反馈回路中串入100 Ω高精度采样电阻，通过测量采样电阻两端的电压来测量系统输出 If．在－0.6 Oe～+0.6 Oe范围内，反复调节，测量取得正行程和逆行程输出电压，数据如表1所示．

表1 实验测量数据

采用最小二乘法对数据进行拟合，拟合曲线如图5所示，得到拟合方程为

传感器满量程输出、灵敏度、线性度分别为其中:(ΔVout)max为输出平均值与拟合直线的最大偏差．

若该传感器仅使用比例控制，则可以得到传感器的性能指标如下:灵敏度K≈1.111 V/Oe，线性度δL=0.28%．可见，当传感器采用比例积分控制器时，传感器的性能指标具有较大的提升．

图5 测量拟合曲线

4 结论

1)基于钴基非晶材料显著的巨磁阻抗效应，设计并实现了一种带有闭环负反馈结构的磁场测量传感器．

2)研究了传感器各部分的特性，并给出了传感器的数学模型．以该模型为基础，考虑了传感器在常值输入时的误差传递函数，对比比例控制规律以及比例积分控制规律作用下传感器的稳态误差．比例积分控制规律消除了传感器在常值输入下的稳态误差，有效地提高了传感器的线性度．

3)实验表明比例积分控制器有效地改善了传感器的性能指标，使传感器的灵敏度达到1.759 V/Oe，线性度达到0.16%．

［1］ MOHRI K，KAHZAWA T，KAWASHIMA K．Magneto-inductive effect(MI effect)in amorphous wires［J］．IEEE Transaction on Magnetics， 1992，28(5):3150－3152．

［2］ KNOBEL M，PIROTA K．Giant magnetoimpedance:concepts and recent progress［J］．Journal of Magnetism and Magnetic Materials， 2002，242－245:33－40．

［3］ PAL S，MANIK N，MITRA A．Dependence of frequency and amplitude of the AC current on the GMI properties of Co based amorphous wires［J］．Materials Science＆ Engineering， 2006，415(1):195－201．

［4］ ZHOU Z M，ZHOU Y，CHEN L．Perpendicular GMI effect in meander NiFe and NiFe/Cu/NiFe film［J］．IEEE Transactions on Magnetics， 2008，44(10):2252－2254．

［5］ GARCIA C，ZHUKOVA V，GONZALEZ J，et al．High-frequency GMI effect in glass-coated amorphous wires［J］．Journal of Alloys and Compounds， 2009，488(1):9－12．

［6］ CORODEANU S，OVARI T，LUPU N，et al．Magnetization process and GMI effect in as-cast nanocrystalline microwires［J］．IEEE Transactions on Magnetics， 2010，46(2):380－382．

［7］ MOHRI K，PANINA I V，UCHIYAMA T，et al．Sensitive and quick response micro magnetic sensor utilizing magneto-impedance in Co-rich amorphous wires［J］．IEEE Transactions on Magnetics， 1995，31(2):1266－1275．

［8］ BOUKHENOUFA A，DOLABDJIAN C，ROBBES D．High-sensitivity giant magneto-inductive magnetometer characterization implemented with a low-frequency magnetic noise-reduction technique［J］．IEEE Sensors Journal， 2005，5(5):916 －923．

［9］ MALATEK M，RIPKA P，KRAUS L．Temperature offset drift of GMI sensors［J］．Sensors and Actuators A:Physical， 2008，147(2):415 －418．

［10］ DING L H，SAEZ S，DOLABDJIAN C，et al．Equivalent magnetic noise limit of low-cost GMI magnetometer［J］．IEEE Sensors Journal， 2009，9(2):159 －168．

［11］ 赵湛，鲍丙豪，徐云峰，等．钴基非晶磁芯巨磁阻抗效应电流传感器［J］．仪器仪表学报， 2007，28(3):483－488．

［12］ 李刚．非晶丝地磁传感器研究［D］．哈尔滨:哈尔滨工业大学，2009．

Research of magnetic sensor based on GMI effect

XIE Wei-nan1，LIANG Hui-min2

(1．Space Control and Inertial Technology Research Center，Harbin Institute of Technology，150080 Harbin，China，xieweinan@hit．edu．cn;2．School of Electrical Engineering and Automation，Harbin Institute of Technology，150001 Harbin，China)

Based on the giant magneto-impedance principle of amorphous materials，a novel magnetic sensor is presented and developed．According to double peaks feature of the amorphous，the working principle is analyzed．The sensor structure with closed loop negative feedback is designed，and the mathematical model of the sensor is deduced．By analyzing the error transfer function of the sensor，PI controller is proposed，which can eliminate the steady state error and improve the linearity．The experimental results show that the performance of the sensor is improved by PI controller．The linearity is within 0.2%and the sensitivity is up to 1.759 V/Oe．

magnetic sensor;giant magneto-impedance effect;amorphous

TP212

A

0367－6234(2011)08－0109－04

2010－05－30．

中国博士后科学基金资助项目(20090460908)．

解伟男(1979—)，男，讲师;

梁慧敏(1971—)，女，教授，博士生导师．

(编辑 魏希柱)