超大跨度悬索桥二维颤振频域直接分析方法

邵亚会，葛耀君，柯世堂

(同济大学土木工程防灾国家重点实验室，200092上海，yahuishao@hotmail．com)

超大跨度悬索桥二维颤振频域直接分析方法

邵亚会，葛耀君，柯世堂

(同济大学土木工程防灾国家重点实验室，200092上海，yahuishao@hotmail．com)

为改善传统复模态特征值分析方法(CEVA)求解二维颤振问题时迭代不收敛和运算时间较长的问题，基于传统复模态特征值分析方法和费拉里求解一元四次方程的思路，提出了二维颤振频域直接分析方法(Straight forward method)，在超大跨度悬索桥二维颤振分析中无需频率的预先选取和迭代求解，计算时间短．采用该方法对闭口钢箱梁、理想平板、中央开槽钢箱梁、中央双开槽钢箱梁这4种典型断面各6种跨度的悬索桥进行二维颤振频域直接分析．结果表明:从颤振稳定性能的要求出发，跨度小于1 500 m的悬索桥可采用闭口钢箱梁，跨度小于3 000 m的悬索桥需采用单开槽钢箱梁，跨度大于3 000 m的悬索桥需采用双开槽钢箱梁．

二维颤振;超大跨度悬索桥;直接分析方法;频域

桥梁断面属非流线型断面，当气流经过时，流体和固体相互作用，形态十分复杂，为了求解此类分离流颤振问题，Scanlan等［1］提出了基于风洞试验6个气动导数的非定常气动力表达式．Scanlan在进行颤振求解时，采用的是半逆解法．K．Wilde等［2］在进行二维颤振机理的研究过程中采用二自由度的状态空间复模态特征值求解方法(CEVA方法)，将二自由度颤振体系的振动响应表达为复模态叠加的形式．文献［3－4］采用了与此相同的方法．该方法的缺点是:当悬索桥跨度增加，柔性增强，扭弯频率比接近于1时，复频率的迭代可能会出现不收敛的情况;迭代求解频率的做法，需花费较多时间．文献［5－8］提出了二维颤振频域分析的分步分析方法(SBS方法)，与传统复模态特征值方法(CEVA方法)不同的是，该方法将颤振分析分解为扭转振动分支和竖向振动分支，在各分支中考虑扭转和竖向2个自由度的相互耦合效应，该方法的优点在于可以分析不同的颤振导数在结构颤振稳定中所发挥的作用．SBS方法在求解特征值问题上仍然是采用频率的迭代算法．考虑到二维颤振复模态分析方法的关键问题在于求解关于系统振动频率的特征方程，而特征方程是标准一元四次方程，因此可以借鉴费拉里求解四次方程的方法，基于Scanlan二维颤振理论框架和二自由度状态空间复模态求解思路，建立不需频率迭代的超大跨度悬索桥二维颤振直接分析方法，并分析超大跨度悬索桥的颤振性能和颤振形态随中跨跨度、加劲梁断面形式等的变化规律．

1 二维颤振频域直接求解

二维颤振分析和节段模型风洞试验，是研究桥梁颤振性能的常用手段，桥梁节段模型风洞试验悬挂模型如图1所示，二维桥梁断面颤振分析模型如图2．

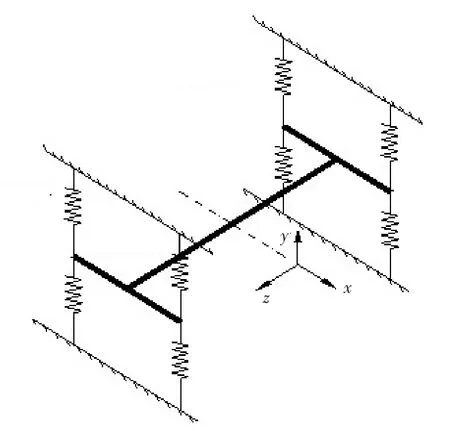
图1 二维节段模型风洞试验示意图

二维颤振分析模型有竖向h和扭转向α二个自由度，运动方程为

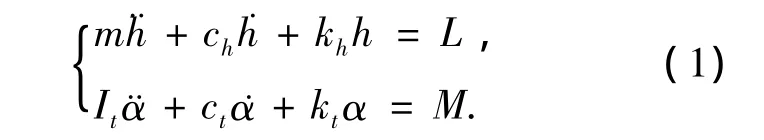
其中:m和It为节段模型延米质量和质量惯矩;kh和kt分别为竖弯和扭转刚度;ch和ct分别为竖弯和扭转阻尼比;L和M分别为延米气动升力和升力矩．

图2 二维桥梁断面颤振分析模型

基于小位移和攻角不变假定的Scanlan气动自激力的频域表达式为

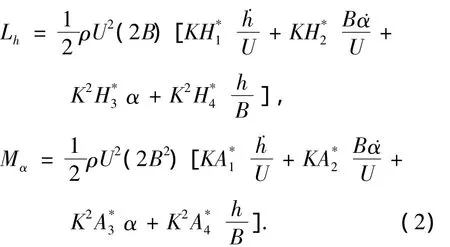
其中:ρ为空气密度;U为来流平均风速;B为桥梁宽度;K=Bω/U，是无量纲折减频率;ω为振动圆频率;h和α分别为桥梁断面的竖向和扭转位移;H*和A*分别为竖弯向和扭转向气动导数．

二维桥梁节段模型的颤振运动方程转化为

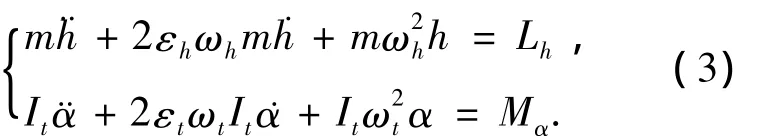
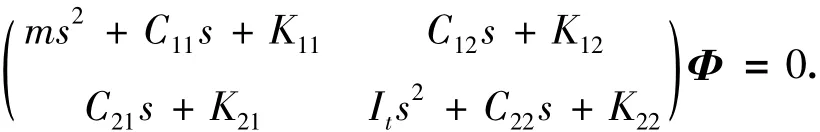
则复特征值问题转化为求解以下一元四次方程的问题:

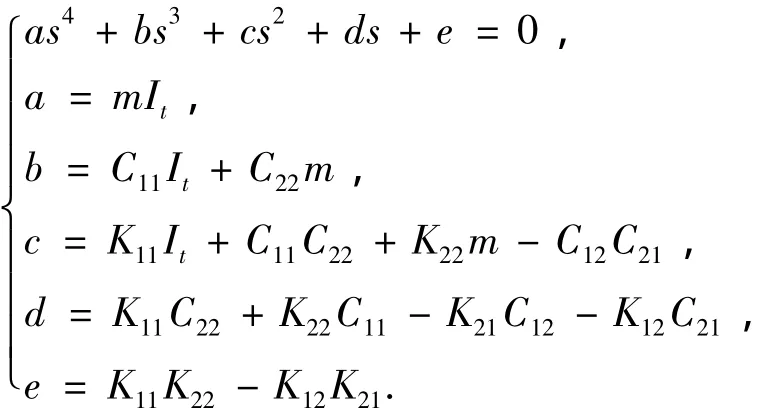
求解该方程的步骤分为

1)将方程转化为无三次项的四次方程:

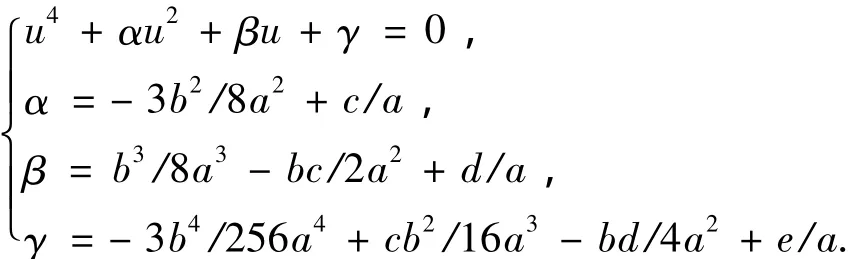
2)将方程转化为三次方程:

求解出特征值和特征向量之后，即得到了二维颤振系统随风速变化的振动频率和振动阻尼比，而振动系统在颤振发散状态之前的每个时刻的运动方程的通解为

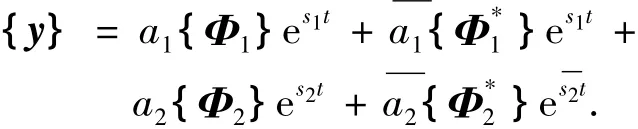
基于上述求解过程，可编制二维颤振频域直接分析方法的程序(Straight forward method)．

2 悬索桥参数化模型建模与动力性能

为研究超大跨度桥梁随着跨径增加，其颤振性能的变化规律，本文采用APDL语言建立了超大跨度悬索桥有限元参数化模型，如图3所示．加劲梁、桥塔采用空间梁单元模拟;主缆和吊杆采用空间杆单元模拟．主缆、加劲梁的质量和几何参数，按照满足悬索桥挠度理论静力条件来取值［9－13］，以保证全桥模型的可行性．只需修改参数即可得到满足静力要求的结构尺寸，并快速找到初始平衡状态．

图3 超大跨度悬索桥有限元参数化模型

以矢跨比1∶10为例，求得的自由振动频率如图4所示．随跨径的增大，各阶振动频率的值逐渐接近;侧向振动频率下降的速率最快，跨径大于1 500 m时，正对称侧向振动频率将最先出现，这说明随着跨径的增加，悬索桥侧向刚度降低非常迅速;扭转振动频率随跨径增加变化次之，跨度在1 000～4 000 m之间，正对称扭转振动的出现总是先于反对称扭转振动，但在5 000 m左右跨度时，反对称扭转振动和正对称扭转振动频率不相上下;竖向振动频率随跨径的增加变化相对较小．采用规范公式积分得到的各阶广义质量如图5所示．虽然反对称竖弯振动频率一直小于正对称竖弯振动频率，但是二者对应的竖向广义质量却随跨度不同而交替着先后出现，无固定规律．跨度小于3 000 m的悬索桥反对称扭转广义质量大于正对称扭转广义质量，而3 000～5 000 m跨度范围的悬索桥可能出现反对称扭转振动频率较小的情况．

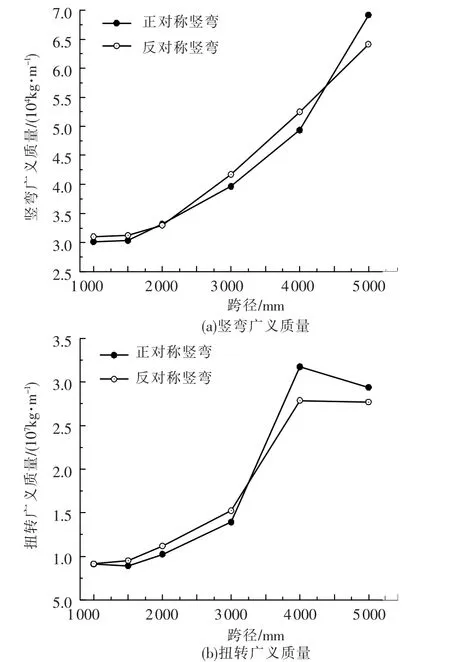
图5 悬索桥质量参数随跨径的变化

3 超大跨度悬索桥二维颤振性能

分别取4种具有代表性的桥梁断面，即江阴大桥闭口钢箱梁断面、理想平板断面、西堠门单开槽钢箱梁断面和墨西拿海峡大桥双开槽钢箱梁断面，采用本文二维颤振直接分析方法(Straight forward method)进行颤振分析，研究悬索桥不同跨度范围、不同断面形式的颤振临界风速、颤振频率等问题．

不同跨度，不同断面形式的悬索桥的颤振临界风速见表 1，系统二阶振动阻尼比随风速的变化如图6所示．

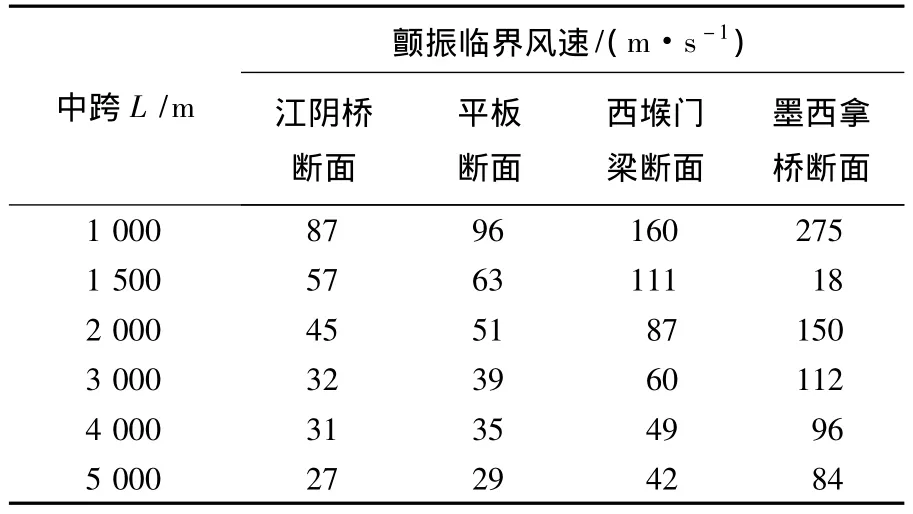
表1 颤振临界风速随跨径的变化

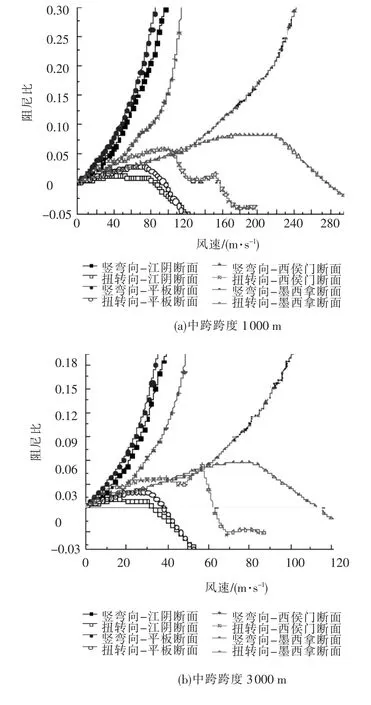
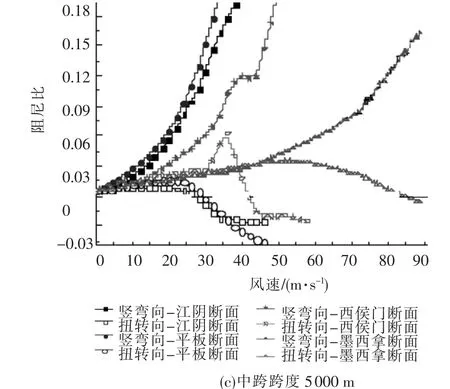
图6 系统自由振动阻尼比随风速的变化

研究发现:系统竖弯向阻尼比随着风速的增加逐渐增大;扭转向阻尼比随着风速的增加总体呈现先增加后减小的趋势．相同断面、不同跨度的悬索桥的阻尼比－风速曲线形状基本保持不变，只是幅值大小有所变化．双开槽断面的颤振临界风速最高，单开槽断面次之，平板断面再次之，闭口断面最低．双开槽断面具有很好的颤振稳定性能，是超大跨度悬索桥理想的断面形式．对于1 000 m跨度的悬索桥，4种断面形式都能满足颤振稳定性能的要求，可不考虑开槽措施;跨度增加到1 500 m左右时，非开槽断面的临界风速最大为63 m/s，而开槽断面分别为 111、180 m/s，这以跨度范围建议采取单开槽断面;跨度为2 000 m左右时，非开槽断面已经不能满足颤振稳定性的要求，必须采取开槽措施，单开槽和双开槽都可满足要求;跨度在3 000～5 000 m之间时，建议采取双开槽断面．

4 结论

1)提出悬索桥二维颤振直接分析方法(Straight forward method)，采用费拉里求解四次方程的方法求解四次广义特征值问题，该方法无需颤振频率的选取和迭代求解，对求解超大跨度悬索桥二维颤振问题方便有效．

2)建立悬索桥有限元参数化模型，该模型灵活可变性强，通过控制参数可以建成任意几何参数、质量参数、刚度参数的悬索桥模型，并能同时进行非线性静力计算、考虑预应力的模态计算、模态输出、积分求解广义质量参数等．

3)对1 500 m跨度以下的悬索桥采用非开槽箱形断面可以满足颤振稳定性能的要求;1 500～5 000 m跨度的悬索桥建议采取开槽措施，尤其对于跨度在3 000～5 000 m的悬索桥，建议采取类似于墨西拿桥断面的双开槽措施．

［1］SCANLAN R，TOMKO J．Airfoil and bridge deck flutter derivatives ［J］． Journal of Engineering Mechanics， 1971，97(6):1717－1737．

［2］WILDE K，FUJINO Y，MASUKAWA J．Time domain modeling of bridge deck flutter［J］．Structural Engineering Earthquake Engineering， 1996，13:93－104．

［3］XIANG H，ZHANG R．On mechanism of flutter and unified flutter theory of bridges［C］//Wind Engineering into the 21st Century．Rotterdam:［s．n．］，1999:1069 －1074．

［4］YANG Y，GE Y，XIANG H．Coupling effects of degrees of freedom in flutter instability of long-span bridges［C］//Proceeding of the 2nd International Symposium on Advances in Wind ＆ Structures．Busan:Techno Press，2002:625－632．

［5］MATSUMOTO M，NIHARA Y，KOBAYASHI Y，et al.Flutter mechanism and its stabilization of bluff bodies［C］//Proceedings of the Ninth International Conference on Wind Engineering．New Delhi，India:［s．n．］，1995:827－838．

［6］MATSUMOTO M，HAMASAKI H，YOSHIZUMI F．On flutter stability of decks for super long-span bridge［J］．Structural Engineering Earthquake Engineering， 1997，14:185－200．

［7］MATSUMOTO M，DAITO Y，YOSHIZUMI F，et al.Torsional flutter of bluff bodies［J］．Journal of Wind Engineering＆ Industrial Aerodynamics， 1997，69:871－882．

［8］MATSUMOTO M，MIZUNO K．Flutter instability and recent development in stabilization of structures［J］．Journal of Wind Engineering and Industrial Aerodynamics， 2007，95:888－907．

［9］YONEDA M，MANABU I．Effects of dead weight on aerodynamic stability of long-span suspension bridges［J］．Structural Engineering Earthquake Engineering， 1986，3(1):135－145．

［10］CLEMENTE P，NICOLOSI G，RAITHEL A．Preliminary design of very long-span suspension bridges［J］．Engineering Structures， 2000，22(12):1699 －1706．

［11］DEL ARCO D，APARICIO A．Preliminary static analysis of suspension bridges［J］．Engineering Structures， 2001，23(9):1096－1103．

［12］XIANG H，GE Y．Refinements on aerodynamic stability analysis of super long-span bridges［J］．Journal of Wind Engineering ＆ Industrial Aerodynamics， 2002，90:1493－1515．

［13］丁泉顺，大跨度桥梁耦合颤抖振响应的精细化分析［D］．上海:同济大学，2001．

Straight forward method for two-dimensional flutter analysis of super-long-span suspension bridge in frequency domain

SHAO Ya-hui，GE Yao-jun，KE Shi-tang

(State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，200092 Shanghai，China，yahuishao@hotmail．com)

The conventional eigen value analysis method(CEVA)has some shortcomings in solving two-dimensional coupled flutter problems，for example，when the frequency ratio of torsional to bending is approaching 1，the pre-selection of frequency and its iteration is a time consuming work．This paper presents an straight forward method for analyzing two-dimensional coupled flutter of super-long-span suspension bridges，utilizing CEVA method and Ferrari’s thoughts on solving univariate equations of four degrees，which has both improvements on work process and work time compared with the CEVA method．Case studies of four different cross section suspension bridges(the ideal plate，close steel box，single slotted steel box，and double slotted steel box)are provided to validate the developed procedure as well as to demonstrate the flutter analysis of super-long-span suspension bridges using straight forward method．The proposed method in this paper enables the researchers to make comparison on the flutter modality，flutter stability performance and freedom coupling extent of suspension bridges with different mid-span and different cross sections．

two-dimensional flutter;super-long-span suspension bridges;straight forward method;frequency domain

U441

A

0367－6234(2011)08－0119－05

2009－12－29．

国家自然科学基金重大研究计划项目(90715039)．

邵亚会(1981—)，女，博士研究生;

葛耀君(1958—)，男，教授，博士生导师．

(编辑 魏希柱)