基于小波能量传递函数谱的结构损伤识别
2011-07-18毛晨曦周文松欧进萍
毛晨曦,周文松,欧进萍 ,3
(1.中国地震局 工程力学研究所,150080哈尔滨,maochenxi@iem.ac.cn;2.哈尔滨工业大学土木工程学院,150090哈尔滨;3.大连理工大学土木水利学院,116024辽宁大连)
基于小波能量传递函数谱的结构损伤识别
毛晨曦1,2,周文松2,欧进萍2,3
(1.中国地震局 工程力学研究所,150080哈尔滨,maochenxi@iem.ac.cn;2.哈尔滨工业大学土木工程学院,150090哈尔滨;3.大连理工大学土木水利学院,116024辽宁大连)
为排除小波识别结构频率时地震动频带的干扰,提出了小波能量传递函数谱方法.该方法首先将地震动输入和结构地震反应小波谱分别沿时间轴积分,得到结构输入和输出的小波能量谱;然后将结构反应小波能量谱除以地震动输入小波能量谱,并定义为结构小波能量传递函数谱,该谱的脊线即为结构的时变频率.分别采用小波变换直接识别法和小波能量传递函数谱方法对一幢6层砌体结构在汶川地震一系列余震中的频率变化进行识别.结果表明,结构频率在较大的余震中明显降低,说明结构损伤有进一步发展.该方法可有效排除结构地震反应小波谱中地震动频带的干扰,准确识别结构在地震作用过程中的时变频率.
地震;结构余震响应监测;小波能量传递函数谱;损伤识别
小波变换是识别非线性系统时变频率的有效工具[1-4],但在识别建筑结构在地震动作用下发生损伤过程中的时变频率时,简单地对结构地震响应进行小波变换处理识别结果很不理想.这主要因为地震动是窄带随机过程,其频带干扰很难从结构地震响应的小波谱中排除掉,因而也就无法准确识别结构时变频率.为解决这一问题,本文提出了小波能量传递函数谱的概念,并采用这种方法对位于四川省广元市的一幢6层砌体结构在汶川地震后一系列余震中的地震响应进行分析,成功排除了结构响应信号小波谱中地震动输入的频带干扰,准确识别了结构在各次余震中的频率变化.
1 小波能量传递函数谱
1.1 连续小波变换
若信号f(t)为能量有限信号,即f(t)满足
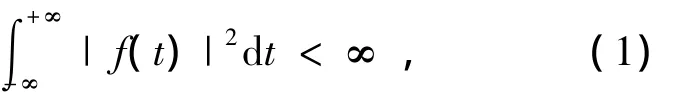
则f(t)的连续小波变换定义为
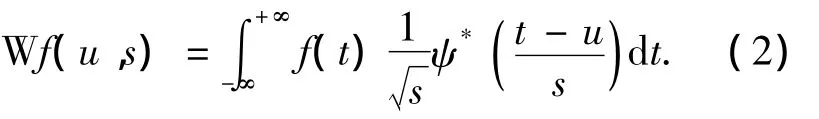
式中:u,s分别为位置参数和尺度参数,ψ*(t)为小波函数ψ(t)的复共轭.
本文中的小波函数采用Gabor小波,即
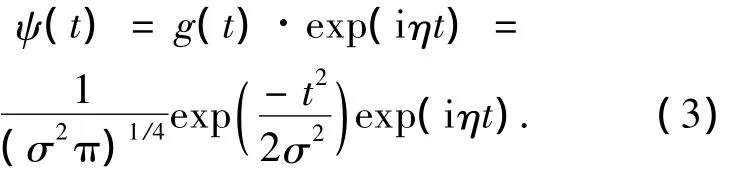
其中:η为频率调制参数,g(t)为高斯窗函数,其傅立叶变换为

对任一实信号f(t)都可以写成振幅a(t)与时变相位 φ(t)的乘积[5],即

式中:a(t)≥ 0,ω(t)=φ(t)'≥0.
将式(3)、(5)代入式(2)并利用傅立叶变换的性质可得到f(t)的Gabor小波变换为
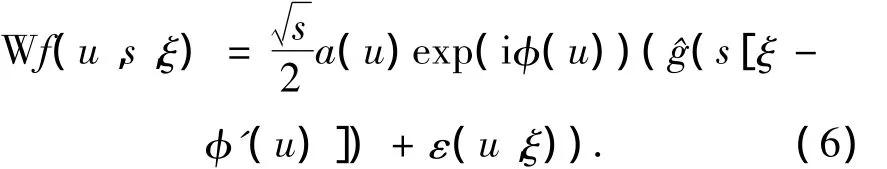
其中:(ξ= η/s),ε(u,ξ)为校正项,当 a(u)、φ'(u)在φu,s的支集内有较小的变差,且 φ'(u)≥Δω/s时,可以忽略不计.Δω为(ω)的带宽,当|ω|>Δω时(ω)≪1.为了简化,记
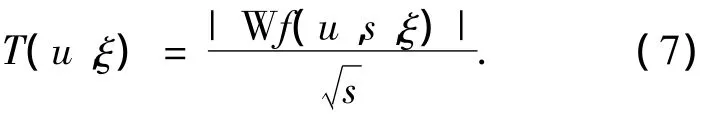
将上式中的Wf(u,s,ξ)用式(6)代入并忽略校正项 ε(u,ξ),得
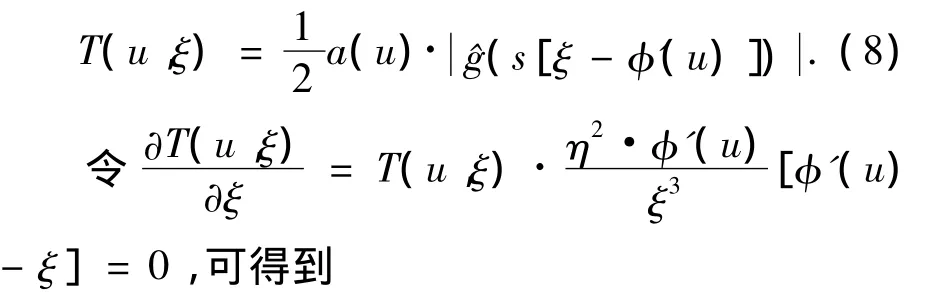

此时相应的点 (u,ξ(u))称之为小波脊.将ξ=η/s代入上式可以进一步得到
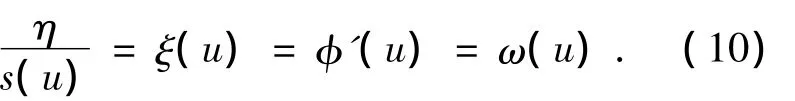
从式(9)可以看出,在时频平面内信号的小波变换的脊(u,ξ(u))就对应着其瞬时频率的曲线(u,ω(u)),所以对于任一实信号,不管其频率在整个时域上是恒定的或时变的,总可以根据此信号的小波脊得到其瞬时频率曲线.具体的小波脊抽取算法参考文献[6].
1.2 小波能量传递函数谱
由于地震动为窄带随机过程,单纯对结构实测地震响应信号进行小波变换处理很难排除地震动的频带干扰,因而也很难准确识别出结构本身的自振频率,为了解决这一问题,本文提出小波能量传递函数谱的概念,并利用小波能量传递函数谱识别建筑结构在地震动激励下的时变频率.所谓结构的小波能量传递函数谱就是结构的传递函数在小波域的表达.如果将建筑结构看做一个线性或非线性的力学系统,当其遭受地震动激励时,其地震动激励和地震响应的小波变换可表达为
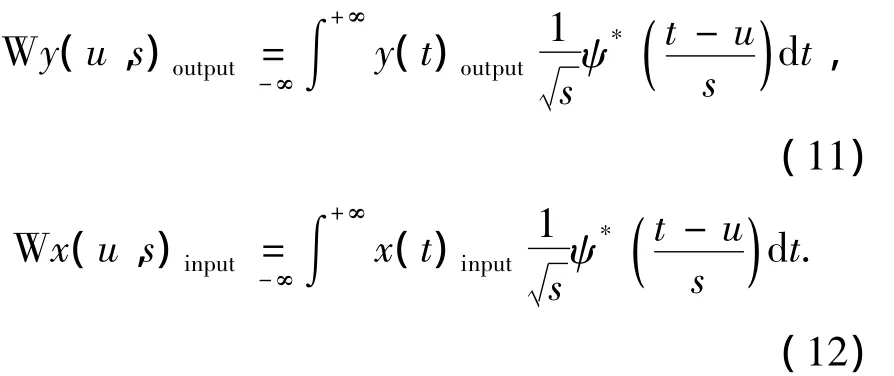
其中:y(t)output为结构地震响应时程,x(t)input为地震动激励时程,Wy(u,s)output、Wx(u,s)input分别表示结构地震响应和地震动激励的小波变换系数,其时频展开即为结构地震响应和地震动激励的小波谱.考虑式 (11)、(12)Wy(u,s)output、Wx(u,s)input的位置参数u与小波谱的时间参数相对应,而尺度参数s则与信号的频率存在对应关系,为方便推导,将 Wy(u,s)output、Wx(u,s)input分别表示为 Wy(t,ω)output和 Wx(t,ω)input的形式,ω为信号的频率.
因为式(11)、(12)中的结构地震响应和地震动激励的小波谱中均含有噪声成分,因而直接将二者相除无法准确得到结构传递函数在小波域的表达,为解决这一问题,本文提出在结构地震响应和地震动激励的小波谱中对每一频率成分对应的小波系数分别进行沿时间轴的积分,即
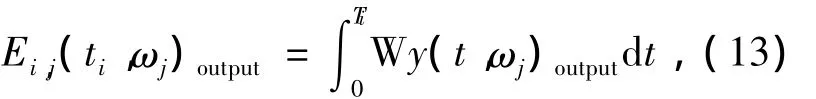

其中:积分区间Ti为信号起始时刻至每一采样点的持续时间;i为所分析信号的采样点序数,其取值为1≤i≤N,N为信号采样点数目;j为进行积分处理的小波系数对应的频率(或称尺度)参数序数;积分所得系数 Ei,j(ti,ωj)output反映了结构响应信号小波谱中频率为ωj的信号成分在截至ti时刻沿时间轴的累积能量,其时频展开称为结构响应的小波能量谱,同样 Ei,j(ti,ωj)input则为结构地震动激励小波谱中频率为ωj的信号成分在截至ti时刻沿时间轴的累积能量,其时频展开称为地震动激励的小波能量谱.
参考结构频域传递函数的概念,定义结构响应输出小波能量谱除以地震动激励小波能量谱为结构在小波域的传递函数,即
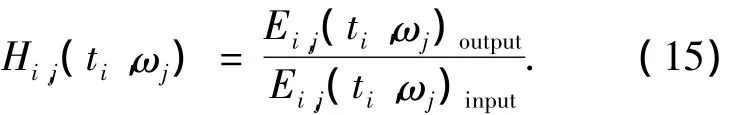
系数Hi,j(ti,ωj)沿时频轴的展开即为结构的小波能量传递函数谱,因为排除了地震动输入的频带干扰,因而小波能量传递函数谱的脊线能较好反映结构的时变频率.采用与小波谱脊线抽取算法相同的方法抽取小波能量传递函数谱的脊线,即为结构时变频率.
2 广元市地震局家属楼余震响应监测
2.1 结构概况及地震响应监测系统
四川省广元市地震局家属楼为6层砖砌体结构,建于1991年,该建筑体型规则简单,在汶川地震中遭到轻微破坏,广元市距汶川地震震中240 km,汶川地震后余震一直比较频繁,图1为该建筑的平面和立面图.2008年9月在该建筑上安装了一套结构地震响应监测系统,该系统包括6个单向和2个三向力平衡加速度传感器,及相应的数据采集、信号调理系统和软件.所采用的力平衡加速度传感器工作频率为0.1~120 Hz,量程为 -2g~2g.6个单向加速度传感器分别放置在结构的1~6层楼板处,因考虑结构短边方向(图1中的y方向)抗侧刚度较小,该方向地震动响应较大,因此6个单向加速度传感器全部沿y向布置;2个三向加速度传感器则分别放置在结构的基础顶面和结构顶层,用以分别监测结构的地震动激励和结构顶层加速度响应,并通过顶层2个方向的加速度响应的对比判断结构振动是否存在扭转分量.
2.2 结构余震响应监测结果
表1为结构余震响应监测系统自2008年10月至12月间监测到的各次余震中比较大的10条记录.可以看出2008年12月10日和2008年10月24日发生的震中在青川的2次余震震级较大,在这2次余震中监测到的结构基底沿y向的加速度峰值分别为0.057、0.041 m/s2.
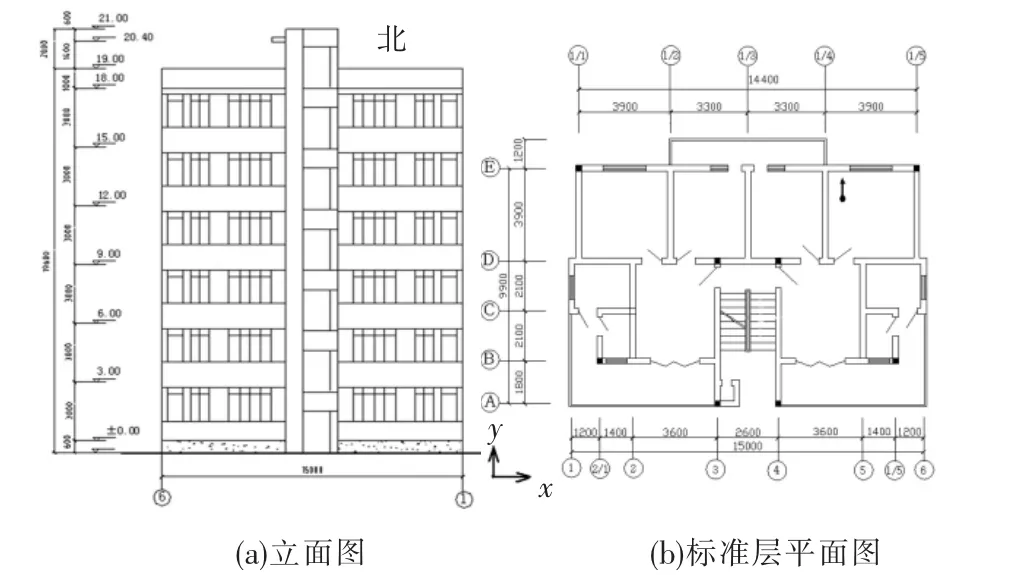
图1 广元市地震局家属楼平面及立面图
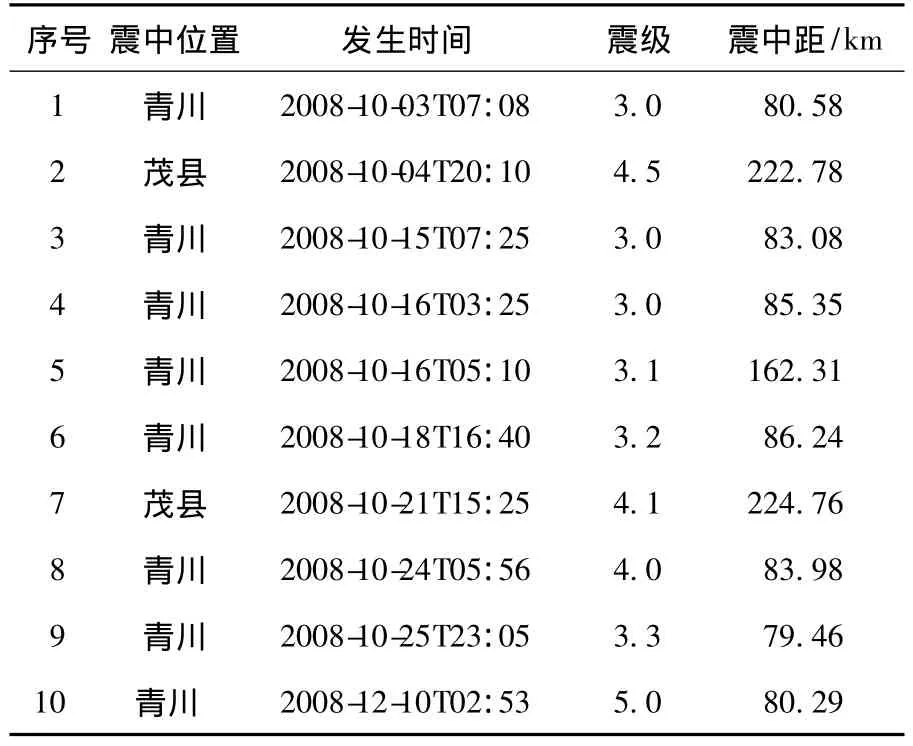
表1 记录余震列表
图2、3绘出了12月10日和10月24日2次余震中结构基底以及各层y方向加速度响应时程.由图可见,在12月10日的余震中,结构顶层y向加速度峰值达到了0.296 m/s2,10月24日余震中,结构顶层y向加速度峰值为0.135 m/s2.
3 基于小波能量传递函数谱的结构时变频率识别
为了识别广元市地震局家属楼在表1所列各次余震中的时变频率,这里首先对该结构的地震响应信号进行Gabor小波变换,并抽取Gabor小波谱的脊线,观察地震动输入信号频带对结构时变频率识别结果的影响;随后采用本文提出的小波能量传递函数谱方法对结构各次余震响应进行处理,识别得到结构时变频率.
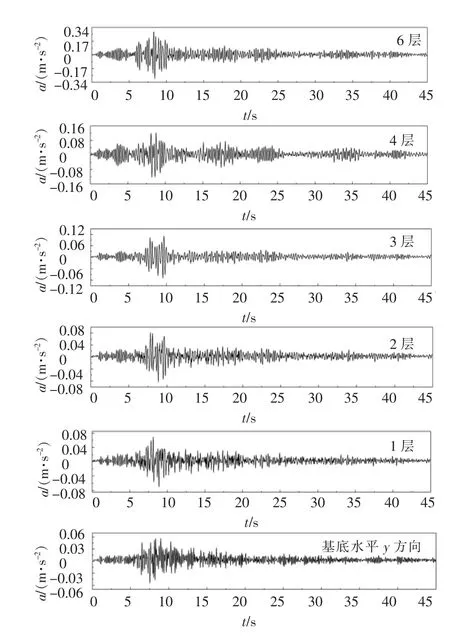
图2 2008年12月10日余震中结构各层y方向加速度时程

图3 2008年10月24日余震中结构各层y方向加速度时程
图4为分别采用上述2种方法识别得到的12月10日余震中该结构频率变化时程.因为可将结构任一层的地震动响应和结构的地震动激励看作结构系统的一对输出和输入,所以根据结构系统任意一对输出和输入均可识别结构频率.这里给出的是根据结构顶层地震动输出和基底地震动激励识别得到的频率时程.图4(a)为仅对结构顶层地震响应进行Gabor小波变换并抽取小波谱脊线识别得到的结构频率时程,从图中虽然可以分辨出结构振动的前两阶频率,但频率时程曲线波动较为剧烈,并且Gabor小波时频谱在结构自振频率以外的频带上也可以看到能量峰值,这些能量峰值与结构系统本身的振动频率无关,因而可以判断出是来自于地震动激励的频带干扰.图4(b)为采用本文提出的小波能量传递函数谱方法识别得到的结构频率时程,从图中可以清楚地看到结构的前两阶频率,其中第一阶频率约为3.27 Hz,第二阶频率约为4.44 Hz,并且在结构地震响应幅值比较大的时间段(5~10 s)第一阶频率出现了下降,约下降8.31%,说明在此次余震中结构损伤有进一步发展,在10 s之后由于地震动激励减小,结构地震响应也相应减小,结构第一阶频率由于损伤裂缝的闭合出现回复.
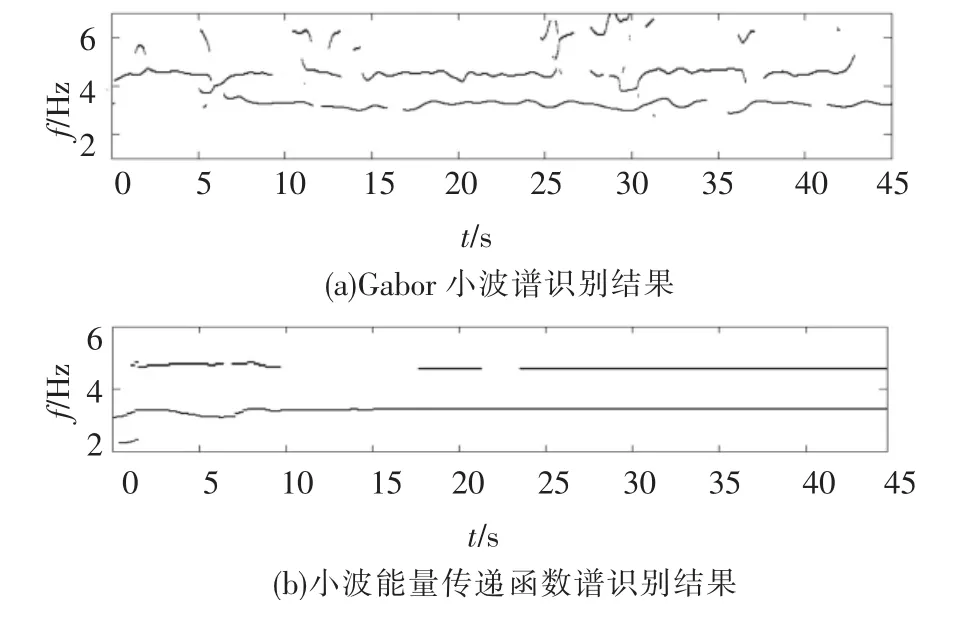
图4 2008年12月10日余震中结构频率变化识别结果
图5为上述结构在2008年10月24日余震中的频率变化时程.其中图5(a)为仅采用Gabor小波谱方法对结构地震动输出进行处理识别得到的结构前两阶频率的时程.从图中可以看出,识别得到的结构第一、二阶频率时程曲线波动十分剧烈,受到地震动激励的频率干扰,导致无法准确识别结构频率.图5(b)则为采用小波能量传递函数谱方法识别得到的结构频率变化时程.结构第一、二阶频率识别结果非常清晰,且同样在结构地震响应幅值较大的时间段(12~17 s)结构第一阶频率出现了下降,下降7.9%,说明在本次余震中结构损伤也出现发展.
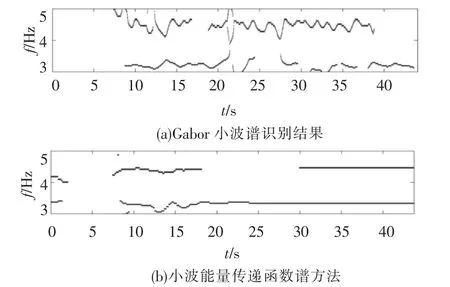
图5 2008年10月24日余震中结构频率变化识别结果
图6为监测得到的广元市地震局家属楼结构在表1所列的部分余震中结构顶层的加速度响应,以及采用小波能量传递函数谱方法识别得到的该建筑在各次余震中的频率变化时程.在各次余震中,只有2008年12月10日和2008年10月24日2次余震中结构的地震响应较大,其他各次余震中结构地震响应均较小.从频率变化时程上看,也只有12月10日和10月24日2次余震中结构一阶频率出现了下降,其他各次余震中结构频率基本没有变化,说明结构在上述2次余震中损伤有进一步的发展.
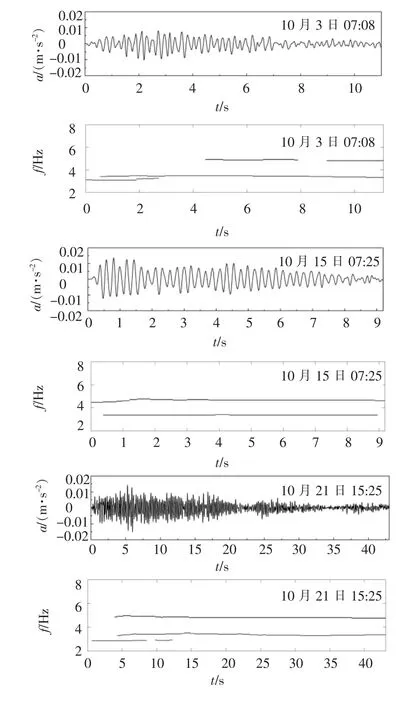
图6 部分余震中的顶层加速度响应和时变频率
4 结论
1)提出了采用小波能量传递函数谱方法排除地震动频带干扰,识别结构在地震动激励下时变频率的新方法.
2)地震动激励属于窄带随机过程,采用传统小波变换方法单纯对建筑结构地震响应信号进行处理无法排除地震动激励的频带干扰,因而也无法准确识别结构在地震作用过程中的频率变化.小波能量传递函数谱方法能成功排除地震动激励的频带干扰,准确识别出结构频率在地震作用过程中的变化时程,从而为进一步的结构损伤识别和评估提供依据.
3)通过安装的结构地震响应监测系统成功监测到了余震响应,采用小波能量函数谱方法识别得到该结构余震中的频率变化时程.结果表明,结构只在震级比较大的余震中损伤出现了进一步发展,在震级比较小的余震中由于地震动激励幅值较小结构损伤没有发展.
[1] GURLEY K,KAREEM A.Applications of wavelet transform in earthquake,wind and ocean engineering[J].Engineering Structures, 1999,21:149-167.
[2]KAREEM A,KIJEWSKI T.Time-frequency analysis of wind effects on structures[J].Journal of Wind Engineering and Industrial Aerodynamics, 2002,90:1435-1452.
[3]KIJEWSKI T,KAREEM A.Wavelet transform for system identification in civil engineering[J].Computer-Aided Civil and Infrastructure Engineering, 2003,18:339-355.
[4]YANG J N,LEI Y,LIN S,et al.Identification of natural frequencies and damping of in site tall buildings using ambient wind vibration data[J].Journal of Engineering Mechanics, 2004,130(5):570 -577.
[5]RUZZENE M,FASANA A,GARIBALDI L,et al.Natural frequencys and dampings identification using wavelet transform:application to real data[J].Mechanical Systems and Signal Processing, 1997,11(2):207 -218.
[6]TCHAMITCHIAN P,TORRESANI B.Ridge and skeleton extraction from the wavelet transform[C]//RUSDAI M B.Wavelets and Their Applications[M].Boston:Jones and Bartlett,1992:123 -151.
Damage assessment based on wavelet energy transfer function spectrum
MAO Chen-xi1,2,ZHOU Wen-song2,OU Jin-ping2,3
(1.Institute of Engineering Mechanics,China Earthquake Administration,150080 Harbin,China,maochenxi@iem.ac.cn;2.School of Civil Engineering,Harbin Institute of Technology,150090 Harbin,China;3.School of Civil and Hydraulic Engineering,Dalian University of Technology,116024 Dalian,Liaoning,China)
A new wavelet energy transfer function spectrum(WETFS)method was proposed in this study to remove frequency contamination of earthquakes from wavelet spectrum of structural responses in identifying frequency variation of structures.First,wavelet spectrums of earthquake excitation and structural response were integrated along time respectively to get wavelet energy spectrum of earthquakes and seismic responses.Then the WETFS was defined by dividing wavelet energy spectrum of earthquake excitation by that of structural response.The ridge on WETFS just represented the variation of structural frequencies.This method and the traditional wavelet method were both applied on frequency identification of one 6-story masonry apartment building.The seismic responses of this building during series of aftershocks of Wenchuan earthquake were measured and structural frequencies were identified to decrease remarkably during two aftershocks.The results of the two methods indicate that the WETFS method can identify variation of structural frequency accurately without contamination of earthquake excitation.
earthquake;structural seismic response monitoring;wavelet energy transfer function spectrum;damage identification
TU362;TN911.6
A
0367-6234(2011)08-0130-05
2010-05-21.
中国地震局中央级公益性研究所基本科研业务费资助项目(2007B15);国家自然科学基金资助项目( 50808165,90915003).
毛晨曦(1974—),女,副研究员;
欧进萍(1959—),男,博士生导师,中国工程院院士.
(编辑 魏希柱)
