L-fuzzy拓扑空间中加强的分离公理

彭瑜



彭瑜

（五邑大学 数学与计算科学学院，广东 江门 529020）

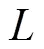
1 引言及预备知识

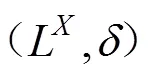
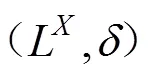
2 加强了的两类分离性

2.1 分明拓扑空间的两类分离性

2.2 加强了的分离性

2.3 加强了的分离性

3 两类分离性的一些性质

证明 类似于定理6的证明.

证明 类似于定理7的证明.

致谢 感谢导师白世忠教授的悉心指导.

[1] 王国俊.-fuzzy拓扑空间论[M]. 西安：陕西师范大学出版社，1988.

[2] 张春燕. LF拓扑空间中一类加强的分离性[J]. 五邑大学学报：自然科学学报，2010，24(1): 57-60.

[3] 陈水利. 拓扑分子格的-分离性[J]. 江汉石油学院学报，1989，11(1): 108-113.

[4] 韩明莲，谭燕华.-Fuzzy拓扑空间的-可数紧性[J]. 天津师范大学学报：自然科学学报，2002，22(2): 31-32.

PENGYu

-fuzzy topological spaces; semi-closed sets; pre-closed sets;-valued-lower semi-continuous functions;-valued-lower semi-continuous functions

1006-7302（2011）02-0006-04

O189.1

A

2010-11-26

国家自然科学基金资助项目（61070150；10971125）；广东省自然科学基金资助项目（8152902001000004）

彭瑜（1987—），女，湖南衡阳人，硕士研究生，研究方向为格上拓扑学.