关于冠图与queens-图的若干结果

2011-07-05邓毅雄

华东交通大学学报 2011年5期

关键词：纵坐标横坐标子图

邓毅雄

（华东交通大学软件学院，江西南昌330013）

Deng Yixiong

（School of Software，East China Jiaotong University，Nanchang 330013，China）

本文讨论的图都是简单无向图，文中未加说明的术语和符号参阅文献[1][2]。

L.W.Beineke等[3]引入了queens-图的概念，并且证明了在一定条件下的完全块图、树、Kn×Pm、Pn×Pm，C2n×Pm等是queens-图，并解决了二部及多部图的问题。到目前，这方面的研究成果比较少，另外的结果有:证明了θ-图是queens-图，并给出了B(m，n，r)图是queens-图的充分必要条件[4]；讨论了queens-图的构造问题，也得到了一些queens-图[5]。

1 定义及引理

设A是（0，1）-矩阵。一个图称为A的queens-图，记为Q(A)，如果这个图的点与A中的1相对应，图的两个点邻接当且仅当A中对应的1同在某线或对角线上。（这里的“线”是指矩阵的行或列。）

我们称一个图G是queens-图，如果存在某（0，1）-矩阵A，使得G是A的queens-图。注意到，给出一个（0，1）-矩阵，很容易获得其对应的queens-图，但是，给出一个图G，判断它是否为queens-图，却常常不是一件容易的事情。所以，这方面研究的一个主要问题是:哪些图是queens-图？

文献[3]给出了下面两个引理:

引理1[3]图G是queens-图当且仅当它的点可以对应坐标(i，j)，并且两个不同的点(i，j)和(k，l)邻接当且仅当1i=k，或 2j=l，或 3i+j=k+l，或4i-j=k-l。

引理2[3]如果图G是queens-图，那么G不包含导出子图K1，5。

引理1给出的4个条件，依次分别指的是两个点在同一行、列、主对角线和斜对角线上，用于queens-图的验证和判断。引理2给出的queens-图的必要条件是基于矩阵只有4条“线”，它在判断一个图不是queens-图时，非常有用。

确定一个图G是否为queens-图，就是构造对应的（0，1）-矩阵A，也就是确定1的位置，或者说是1的坐标(i，j)，而1的位置就是图G的点的位置，所以，图G是否为queens-图，就是看能否构造满足定义或者说满足引理1要求的点的坐标(i，j)。

另外，如果queens-图G对应的（0，1）-矩阵为A，那么A的转置矩阵AT对应的queens-图仍然是G。

悬挂边是度为1的点所关联的边。我们注意到，去掉一个queens-图的悬挂点，就相当于在其对应的（0，1）-矩阵中把该悬挂点所对应的元素“1”改为元素“0”，而这不会影响其它的元素。特别由于它是悬挂点，这个元素的改变，不会影响其它点的结构关系，所以我们有:

引理3 如果G是queens-图，那么去掉G的若干悬挂点所得之子图仍然是queens-图。易知:

引理4 完全图Kn、圈Cn是queens-图。

定义图G的r-正则冠图Ir(G)是指在G的每个点上都粘接r条悬挂边所得之图，而图G的r-弱冠图Ir(G)是指在G的每个点上至多粘接r条悬挂边所得之图。图G的1-正则冠图称为王冠图，记为I(G)。

当G=Kn时，称Ir（Kn）为完全r-冠图；而当G=Cn时，称Ir(Cn)为r-皇冠图，记为Cn⊙rK1。

2 主要结论

根据引理3，易于得到:

定理1 如果冠图Ir(G)是queens-图，那么图G也是queens-图。

由定理1引出问题:如果图G也是queens-图，那么冠图Ir(G)是queens-图吗？显然，一般情况下并不是这样的，这个命题一般是不成立的。下面的定理2给出了一个必要条件，定理3和定理4给出了两类满足这个问题的图。

所谓零图是没有边的图。注意到，当r≥4时，如果G不是零图，冠图Ir(G)含有导出子图K1，5，结合引理2，有

定理2 当G不是零图时，如果冠图Ir(G)是queens-图，那么r≤3。

定理3完全r-冠图I（rKn）是queens-图当且仅当r=1，2，3。

首先，r≤3是Ir(G)是queens-图的必要性由定理1获知。其次，我们证明当r=3时，完全r-冠图Ir(Kn)是queens-图。事实上?

，令各点的坐标分别为

首先，ui(i=0，1，…，n-1)的横坐标均为0，他们相互邻接构成Kn。

注意到，对ui与wi0，它们的横坐标与纵坐标之和为0+(3i+1)=(4i+1)+(-i-1)，则ui与wi0邻接；对ui与wi1，它们的纵坐标均为 3i，则ui与wi1邻接；对ui与wi2，它们的横坐标减纵坐标为0-3i=(9n+2i-5)-(9n+5i-5)，则ui与wi2邻接。

另外，注意到0≤i≤n-1，wi0、wi1、wi2之间横坐标、纵坐标，以及横坐标与纵坐标之和分别均不相同，并且wi0、wi1、wi2的横坐标减纵坐标分别为5i+2、5n+i-2、-3i(i=0，1，…，n-1)，这3组数据之间相互不可能存在相等的情况，根据引理1，wi0、wi1、wi2互不邻接；很容易验证，当j≠i时，wi0、wi1、wi2与uj也均不邻接。

综上，完全 3-冠图I3(Kn)是如上坐标对应的queens-图。

最后，由引理3，我们从完全3-冠图I3(Kn)是queens-图，立即得到完全2-冠图I2(Kn)和完全1-冠图I1(Kn)都是queens-图。

由引理3和定理3，得

推论1 当r≤3时，完全r-弱冠图是queens-图。

定理4 皇冠图Cn⊙rK1是queens-图当且仅当r=1或r=2。

证明首先我们注意到，当r＞2时，Cn⊙rK1含有导出子图K1，5，根据引理2，Cn⊙rK1不是queens-图。类似于定理3的证明，我们只要证明Cn⊙rK1是queens-图即可。

设V(Cn)={u0，u1，…，un-1}，与ui(i=0，1，…，n-1)邻接的2个悬挂点为wij(j=0，1)，而Cn⊙2K1的各点的坐标定义如下:

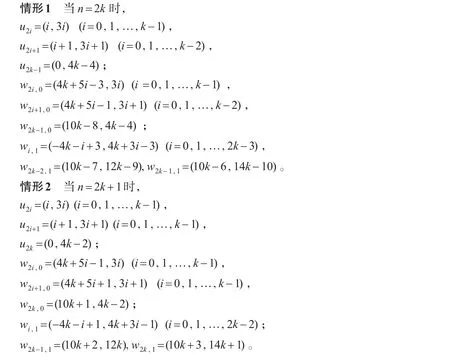
下面验证情形1给出的坐标按照定义得到的queens-图恰好就是图Cn⊙2K1。

首先，对于u2i与u2i+1(i=0，1，...，k-2)，由于i-3i=(i+1)-(3i+1)，所以点u2i与u2i+1(i=0，1，...，k-2)邻接；由于(k-1)+(3k-3)=0+(4k-4)，所以u2k-2与u2k-1邻接；而u0与u2n-1的横坐标均为0，所以u0与u2n-1邻接，故ui(i=0，1，…，2k-1)恰构成圈Cn。

由于ui和wi0(i=0，1，…，2k-1)的纵坐标对应分别相同，所以ui与wi0邻接；且容易验证，当i≠j(i、j=0，1，…，2k-1)时，ui与wj0不邻接。

注意到，由wi1，ui(i=0，1，...，2k-3)的横坐标与纵坐标之和相同，即 (-4k-i+3)+(4k+3i-3)=2i，所以wi1与ui邻接；而u2k-2与w2k-2，1各自的横坐标与纵坐标之差均为 -2k+2，u2k-1与w2k-1，1各自的横坐标与纵坐标之差均为 -4k-4，所以u2k-2与w2k-2，1，u2k-1与w2k-1，1分别邻接；且容易验证，当i≠j(i、j=0，1，…，2k-1)时，ui与wj1不邻接。

同样根据引理1，可以证明wi0、wi1(i=0，1，...，2k-1)均不相互邻接。

类似可以验证情形2。

综上，Cn⊙2K1是queens-图。

由引理3和定理4，得:

推论2 当r=1或r=2，皇冠图Cn⊙rK1的弱冠图是queens-图。

[1]HARARY F.Graph theory[M].NewYork:Addison Wesley，Publishing Company，1969:1-274.

[2]BONDY J A，MURTY U S R.Graph theory with application[M].NewYork:Elsevier Science Publishing Company，1976:1-65.

[3]BEINEKE LW，BROERE I，HENNING MA.Queens graphs[J].Discrete Mathematics，1999，206（1-3）:63-75.

[4]邓毅雄，熊金泉，等.关于Queens-图的若干结果[J].华东交通大学学报，2003，20（1）:82-85.

[5]邓毅雄，周尚超，等.Queens-图的构造[J].华东交通大学学报，2004，21（4）:119-121.

[6] GALLIAN J A.A survey:recent results，conjectures，and open problems in labeling graphs[J].Graph Theory，1989，13（4）:491-504.

[7]胡红亮.图Cn及其r-冠的新的优美标号[J].纯粹数学与应用数学，2010，26（6）:454-457.