机械系统可靠性模糊预计的可视化设计

杨腾达 孙 川

(黄石理工学院机电工程学院，湖北黄石435003)

可靠性设计中重要的一环是可靠性分析，系统薄弱环节与设计缺陷可通过可靠性设计指标的分析与评价来发现和确认，以所获取的信息对可靠性设计进行必要的改进。

随着机械行业的迅猛发展，大型复杂机械系统的可靠性分析的需求越来越多，其重要性日益明显。由于机械系统复杂度的增加，其中不可避免地包含有大量的不可忽视的模糊信息，使得仅仅利用常规可靠性理论对大型复杂机械系统进行可靠性分析不能满足工程实践的需求。因而，探讨模糊数学与常规可靠性设计理论的结合是必然的发展趋势。

在设计初始阶段，机械产品的可靠性数据往往十分缺乏，且可靠性预计本身就具有一定的模糊性，使机械产品的可靠性预计较为困难。因而研究如何将模糊数学应用于可靠性分析是十分有意义的[1-2]。

鉴于模糊综合评判能够较好地运用专家经验和模糊信息[3-5]，本文用它来评估可靠性的影响因素。在评估结果的基础上，再应用模糊推理理论对可靠性的预计值进行推理。该方法尤其适用于复杂机械产品(包括其他产品)设计初期的可靠性预计，从而弥补了现有可靠性预计方法的不足。本文通过示例讨论了其具体应用方法。设计了机械系统可靠性指标模糊预计智能系统，使其能方便地应用于机械工程领域，在实际工程应用中能直接调用智能系统对机械系统的可靠性指标进行分析与计算，为机械工程领域开辟了新的发展方向，减少了工程领域人员的计算量。

1 机械系统可靠性常规预计数学模型

一般而言，大型复杂机械系统都可以简化为由n个相互独立的多单元串联组成的系统。设R(ts)、Ri(ti)、ts、ti、n分别为机械系统可靠度、第i个单元可靠度、系统工作时间、系统第i个单元工作时间、组成系统单元个数，则有:

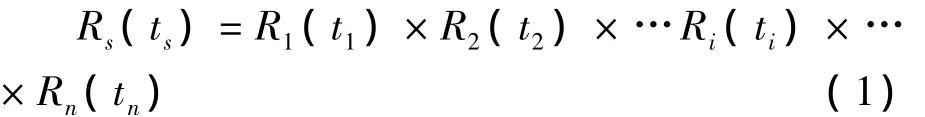
实际工程中，可假定系统工作时间与各单元工作时间相等，即ts=t1=t2=…=ti=…=tn，故:

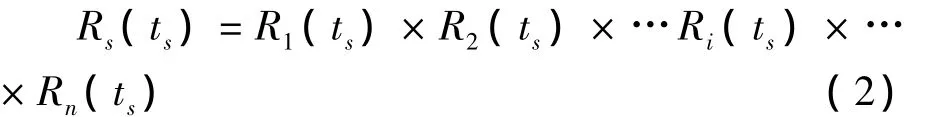
若第m个单元的可靠度Rm(ts)已知，则专家评判后单元可靠度预计值可表示为:

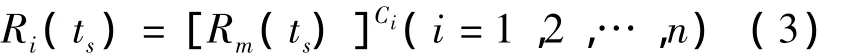
设ωi与ωm分别为第i个单元的综合评级数与已知可靠度的单元的综合评级数，则第i个单元的综合评级因数Ci为:

因此，机械系统可靠度预计值为:

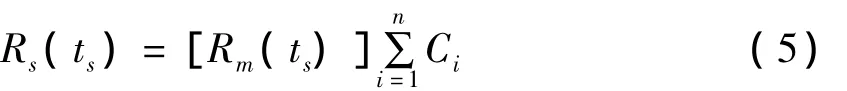
一般而言，机械零部件的寿命不服从指数分布(即失效率不为常数)。在工程实践中，机械系统在正常使用期内，机械零部件的寿命可近似按指数分布处理，特别是在机械系统设计初始阶段，往往可靠性数据缺乏。对大型复杂机械系统进行初步可靠性分析时，为方便，可取系统中各单元失效率为常数，即λi(t)=λi。其失效分布为:

根据已知的第m个单元的失效率 λm，可以预计其他单元的失效率为:

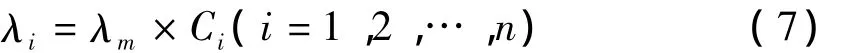
机械系统的可靠度为:

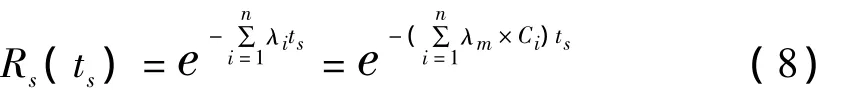
即，由n个相互独立的寿命均服从指数分布的多单元串联组成的大型复杂机械系统其寿命也服从指数分布，失效率为各独立单元失效率之和，亦即:

2 机械系统可靠性模糊预计数学模型

2.1 确定影响综合评级数的因素集

机械系统可靠性分析的首要任务是进行机械系统影响因素分析，确定主要因素，剔除次要因素。机械系统可靠性综合评级影响因子较多，不失一般性，本文仅考虑技术水平a1、重要程度a2、复杂程度a3、环境条件a44个因素，记为a=(a1，a2，a3，a4)。

2.2 确定因素权重集与权重分配

在确定因素集的前提下，综合权衡各权重集因素对机械设计总体的影响，用经验(如专家打分)与统计相结合的方法，完成各因素间权重分配，记为:

2.3 建立模糊关系矩阵

对因素集内各因素所属等级进行评级时，同一因素的级别可用离散等级“高、较高、一般、较低、低”，“好、较好、一般、较差、差”等表示，且记为:

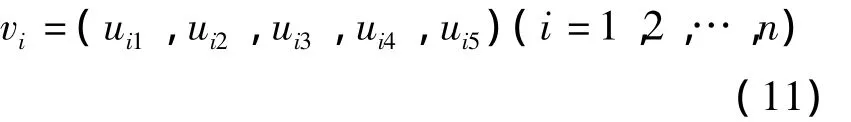
以各因素对综合评级数的作用为基准对每一等级定义其相对隶属度，即为各等级标准值。所有等级的相对隶属度组成一个集合，记为:

相对隶属度越大则单元可靠度越低，失效率越大，综合评级数越大。

对任一因素ai(i=1，2，3，4)采用经验方法(如专家打分)与统计方法获得对因素ai的评级。一般而言，技术水平高，则相应可靠度高、失效率低;单元复杂程度越高，则相应可靠度低、失效率高。因而可对因素集内各因素所属等级进行评级为:

技术水平=(高、较高、一般、较低、低)

重要程度=(重要、较重要、一般、不太重要、不重要)

复杂程度=(低、较低、一般、较高、高)

环境条件=(好、较好、一般、较差、差)

因素集内各因素相对隶属度对应式(12)取值为(0.2，0.4，0.6，0.8，1)。

实际应用中，由于数据处理的需要，必须进行归一化处理，处理结果记为:

对单元所有因素评级即可获得该单元模糊关系矩阵:

式中rij为因素ai与因素等级vij之间的相对隶属度，即模糊关系程度。

2.4 确定单元综合评级数

根据模糊变换原理，可得模糊综合评判模型为:

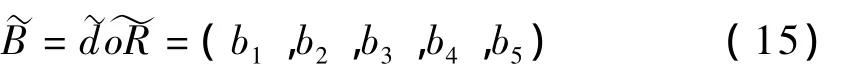
若用实数加乘法计算模型M(·，+)计算，则有:

单元综合评级数可按式(17)来计算。

在获得各单元的综合评级数 ωi(i=1，2，…，n)后，就可进行系统的可靠性预计。

该方法可在机械系统初步设计阶段(即可靠性数据缺乏)的情况下使用。建立预计单元与已知单元之间的可靠性关系，并获得可靠性估计值，为复杂机械系统的设计与分析提供可靠性相关信息。

3 系统设计

系统构成原理如图1所示。

图1 系统构成原理图

3.1 功能模块划分

根据所建立的机械系统可靠性指标的模糊预计分析模型与实际工作需求，本系统的设计主要包含了4大模块的设计，即登录模块、数据输入模块、计算模块和数据输出模块。其中，数据输入模块由权重与相对隶属度输入界面和模糊矩阵参数输入界面组成。计算模块由模糊评判模型计算界面和综合评级数计算界面组成。

3.2 各功能模块之间的关系

系统各功能模块之间的关系如图2所示。

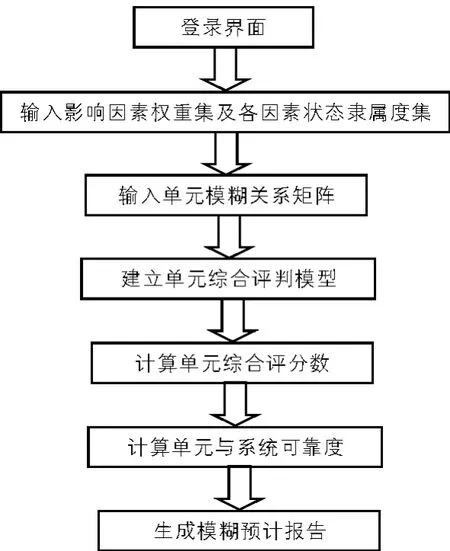
图2 系统功能模块图

3.3 各功能模块的作用

1)登录模块。

登录模块是整个系统的一个功能说明，直观明了地给使用者传达系统的相关信息。

2)数据输入模块。

数据输入模块由权重与相对隶属度输入界面和模糊矩阵参数输入界面组成。在此模块，操作者需输入已知数据，即系统分析的原始数据。

3)计算模块。

计算模块由模糊评判模型计算界面和综合评级数计算界面组成，所设计的系统可根据数据输入界面的相应数据进行数据分析，得出相应事件的模糊评判模型以及系统各单元综合评级数，进而计算单元与系统的可靠度。

4)报告生成模块。

报告生成模块包含模糊预计分析报告界面和数据文件的生成。模糊预计分析报告界面将系统分析的结果进行汇总，自动生成一个模糊预计分析报告，同时本系统分析所得数据可生成电子文档，便于数据文件的归档保存。

3.4 模块界面图

各功能模块如图3～9所示。

图3 登录界面

图4 权重与隶属度输入

图5 模糊矩阵参数输入

图6 模糊评判模型模块

图7 综合评级数模块

图8 可靠度计算模块

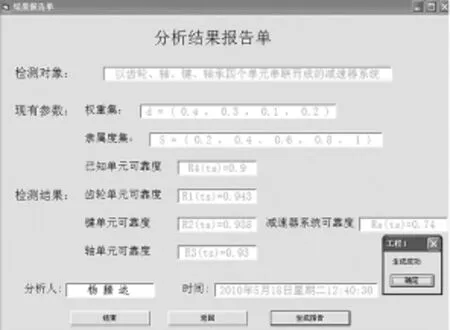
图9 测试结果

4 系统调试运行与实例应用分析

4.1 实例分析

4.1.1 实例

需设计一由齿轮、轴、键和轴承串联而成的减速器。用经验(如专家打分)与统计相结合的方法确定模糊关系矩阵为:

4.1.2 实例常规分析

若设轴承的寿命服从指数分布(分析表明，误差较小)，则轴承的失效率为:

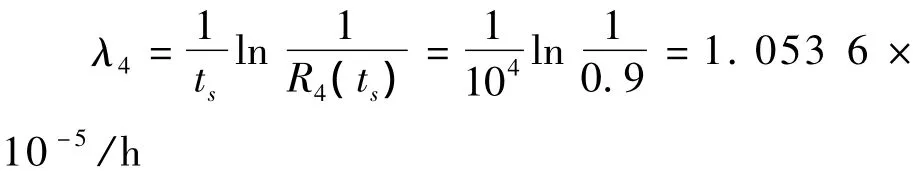
由式(7)预计系统各单元的失效率为λ1=5.901 × 10-6/h，λ2=6.398 × 10-6/h，λ3=6.421×10-6/h。由式(9)预计系统的失效率为λs=2.925 6×10-5/h。根据系统失效率的预计值，求得系统的可靠度为:

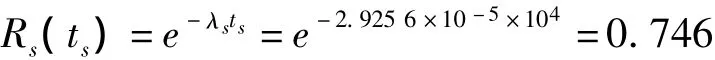
4.1.3 实例模糊分析

由式(17)得各单元的综合评级数分别为:

若轴承的可靠度为 0.9(单元 4)，按式(3)预计齿轮、轴、键的可靠度分别为:

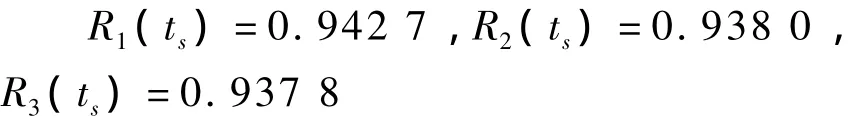
从而按式(2)(或式(5))预计减速器的可靠度为:

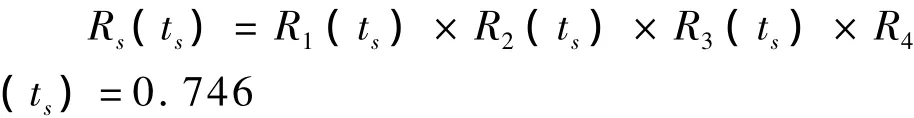
4.1.4 实例常规分析与模糊分析的比较

针对该减速器系统，根据比较成熟的轴承失效率进行常规分析，分别计算齿轮、轴、键的失效率，进而根据系统的失效率预计值来计算系统可靠度为Rs(ts)=0.746。

在模糊分析中，则先通过建立各单元的模糊评判模型，得出其模糊评级数，然后根据比较成熟的轴承的可靠度，分别计算齿轮、轴、键的可靠度，最后根据该串联系统来预计系统可靠度为Rs(ts)=0.746。

由此验证了用本文所给出的模糊分析方法预计系统可靠度的正确性。

4.2 系统运行分析

该系统利用相对成熟的机械零部件可靠性已知数据，用经验(如专家打分)与统计相结合的方法进行综合评级，得到机械系统各单元的模糊关系矩阵，通过可靠度的模糊预计模型的算法来编程，完成系统可靠度的智能计算。

在实例验证中，以理论分析计算由齿轮、轴、键、轴承串联成的减速器来进行验证，在输入减速器系统相关参数后，得到各单元与系统可靠度值(Rs(ts)=0.740)与理论分析值基本一致，故该系统符合要求，运行正常，能对系统可靠度指标进行模糊预计。

5 展望

针对机械工程可靠性设计中的“模糊性”问题，本文主要利用文献[3-6]的研究成果阐明了模糊性的数学处理、模拟方法及模拟结果。所设计的模糊预计智能系统能通过计算机运行对机械系统的可靠性指标进行分析与计算，为机械工程领域开辟了新的发展方向，减少了工程领域人员的计算量。

文中所建立的模糊预计模型和智能系统有一定的局限性，可进行改进和完善。

文中用到的评级预计法模型是以故障率为常数(即寿命均服从指数分布)作为预计系统可靠性的基本假设，不完全符合机械系统可靠性的特点，用于预计机械系统可靠性预计时有一定的局限性。对此，可以采用更科学合理的三参数威布尔分布预计法、耐久性曲线预计法、仿真预计法来替换本模型，提高预计的准确性。

所设计的智能系统，处理对象比较狭窄，缺乏共性能力，需要深入研究并建立带动态参量的数组和函数，简化系统界面的同时，能够处理更一般的机械系统可靠性模糊预计的工程问题。

由于计算小数位数的设置问题，智能系统所得系统可靠度值Rs(ts)=0.740与理论分析值Rs(ts)=0.746略有偏差，可以通过小数位数的设置解决。

[1]Fan Hehong，Sun Xiaohan，Zhang Mingde.A novel fuzzy evaluation method to evaluate the reliability of FIN[C].ICCS 2002.Amsterdam，The Netherlands，2002(2):1247-1251

[2]Eua-Arporn B，Karunanoon A.Reliability evaluation in electrical power generation with uncertainty modeling by fuzzy number[C].Power Engineering Society Summer Meeting.Seattle，Washington USA，2000(4):2051-2056

[3]Xu Qinghua，Li Tao，Sun Chuan，et al.Fuzzy Assessment Method of Professional Skill Based on Feedback Amendment[C].CINC 2010.Wuhan，China，2010(2):360-363

[4]Sun Chuan，Ding Wangjin.Special Skill Evaluation in Mechanical Operation Field Based on Fuzzy Evaluation Method[C].EDT 2010.Shenzhen，China，2010:526-529

[5]孙川.产品成本模糊关系定量分析法[C].第十届工业工程与工程管理国际学术会议(IE＆EM2003)，中国上海，2003:1-4

[6]董玉革.机械模糊可靠性设计[M].机械工业出版社，2000:193-194