一类一阶微分方程的通解及应用*

刘连福

(大连海洋大学，辽宁大连116300)

1 问题与结论

对一阶线性非齐次微分方程:

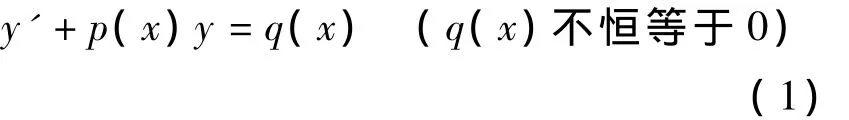
通常采用所谓的常数变易法来求解方程(1)，即令y=u(x)e-∫p(x)dx(这里u=u(x)是x的连续函数，记号∫p(x)dx表示p(x)的某个确定的原函数，以下同)，代入方程(1)求出u(x)，从而得到式(1)的通解[1].

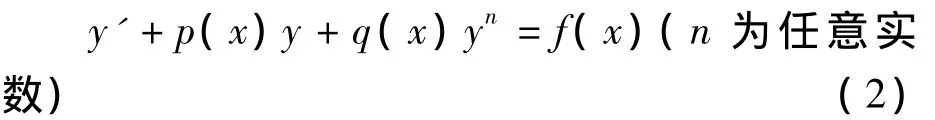
猜想:一般的，对形如方程(2)的一类微分方程在满足某种条件下，也有y=u(x)e-∫p(x)dx这样的通解.

分析 由y=u(x)e-∫p(x)dx得:

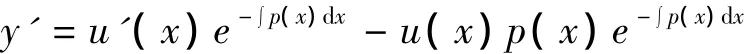
代入方程(2)得:

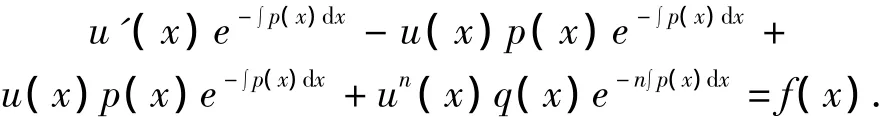
当f(x)=aq(x)e-n∫p(x)dx(a为任意实数)时有:u'e-∫p(x)dx=(a-un)q(x)e-n∫p(x)dx

即u'=(a-un)q(x)e(1-n)∫p(x)dx.

这是一个关于u的可分离变量方程，分离变量，两边积分，求出u=u(x)代入y=u(x)e-∫p(x)dx中就得到方程(2)在条件f(x)=aq(x)e-n∫p(x)dx下的通解.

综合上面分析我们有下面定理.

定理 如果微分方程y'+p(x)y+q(x)yn=f(x)(n为任意实数)中f(x)=aq(x)e-n∫p(x)dx(a为任意实数)，则该方程通解为:y=u(x)e-∫p(x)dx，其中u由可分离变量方程u'=(a-un)q(x)e(1-n)∫p(x)dx确定.

2 应用

2.1 求一阶线性微分方程的通解

对方程y'+p(x)y+q(x)=0，这里n=0，f(x)=0，显然有a=0 使f(x)=aq(x)e-n∫p(x)dx成立，由上面定理知方程通解为:

y=u(x)e-∫p(x)dx，其中u'=-q(x)e∫p(x)dx，两边积分得:u(x)=- ∫q(x)e∫p(x)dxdx+c.

于是一阶线性微分方程通解的通解为:

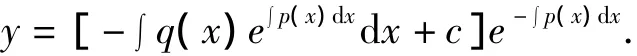
2.2 求伯努利方程的通解

对方程y'+p(x)y+q(x)yn=0(n≠0，1)，这里f(x)=0，显然有a=0 使f(x)=aq(x)e-n∫p(x)dx成立，由上面定理知方程通解为:y=u(x)e-∫p(x)dx，其中u'=-unq(x)e(1-n)∫p(x)dx，分离变量，两边积分得:

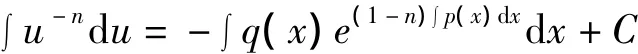
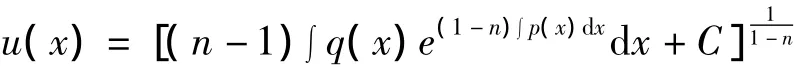
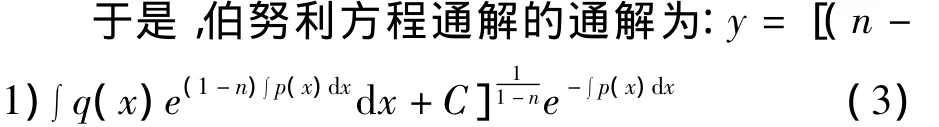
运用方程(3)将简化求伯努利方程通解的计算过程.

2.3 求满足定理条件的黎卡提方程和阿佩尔方程的通解

对黎卡提方程y'+p(x)y+q(x)y2=f(x)和阿佩尔方程[2]y'+p(x)y+q(x)y3=f(x)，如果他们满足定理条件，则其通解为:y=u(x)e-∫p(x)dx，其中u由可分离变量方程u'=(a-un)q(x)e(1-n)∫p(x)dx确定.

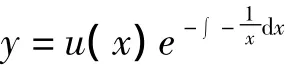
[1]同济大学数学系.《高等数学》(下)[M].北京:高等教育出版社，2008:276-281

[2]洪少春，王永初.基于最优控制反馈系统的Riccati方程的一种求解新方法[J].长江大学学报:自然科学版(理工卷)，2007，4(2):6-8

[3]冯录祥.一类特殊类型Riccati方程的通积分[J].石河子大学报，1997(5):316-318

[4]冯录祥.Riccati方程求积法的一个充分条件[J].怀化师专学报，1999(5):16-17