高导无氧铜杆的冲击拉伸断裂系列实验以及基于样本体积单元的分析*

马东方，侯延军，陈大年，吴善幸，王焕然，贾存威

(宁波大学力学与材料科学研究中心，浙江宁波315211)

基于微空穴成核与增长模型，研究冲击拉伸杆断裂的历史已有30余年。主要问题是:(1)需确定的材料参数太多;(2)对空穴聚集诱发的突变认识不足。随着工程科学的发展，采用损伤力学方法预估准静态拉伸下杆断裂的研究有较大进展。T.Pardoen等［1］研究了弹塑性固体中空穴增长与聚集效应。A.A.Benzerga［2］发展了空穴聚集的微力学框架，其中空穴形状及体积的演化规律按微力学的聚集现象导出。A.R.Ragab［3-4］基于椭球空穴间基体颈缩，提出一种延性断裂模型，并依据一系列材料的无刻槽及有刻槽杆的准静态拉伸实验，确定了很多合金的微力学参数，其中包括空穴的特征体积份额、特征形状因子、平均成核应变等。这些准静态拉伸下杆断裂的微力学研究进展，为研究冲击拉伸杆断裂提供了基础性的技术支撑。陈大年等［5］曾提出一种新的临界冲击拉伸速度实验方法，研究了高导无氧铜的临界冲击拉伸速度，并把A.R.Ragab［3-4］在准静态拉伸下的延性杆断裂模型推广到冲击拉伸下延性杆的断裂，对于较高速度冲击拉伸下包括临界冲击拉伸速度范围的高导无氧铜杆断裂进行了实验与数值研究。本文中，为系统研究高导无氧铜杆在较大速度范围冲击拉伸下的断裂，增加采用拉伸Hopkinson装置的实验结果，试件与冲击拉伸速度均较小，试图与较大试件及较高冲击拉伸速度的实验结果比较。采用样本体积单元的分析方法，并基于对空穴失稳的探讨，试图关联杆的断裂应变。这与A.R.Ragab［3-4］的断裂模型不一样。

1 典型延性材料的冲击拉伸杆断裂实验

对典型的延性材料高导无氧铜(OFHC)进行系列的冲击拉伸杆断裂实验。采用如图1所示的拉伸Hopkinson装置(装置A)，圆管形弹丸以一定速度冲击靶板，靶板牵引入射杆运动。入射杆与透射杆间置OFHC拉伸试件杆，试件两端通过螺纹与入射杆及透射杆连接。当圆筒形弹丸冲击速度足够大时，可引起试件发生拉伸断裂。试件采用圆柱形哑铃状结构，如图2所示，参数列于表1，h为螺纹外径。应该指出，采用如图1所示的拉伸Hopkinson装置研究试件材料的动态本构关系及拉伸断裂时，必须在一定的加载条件下，对试件的几何形状及尺度进行优化设计，使试件内的应力、应变基本上处于均匀状态并减小试件两端过渡区影响。应用LS-DYNA程序［6］，对实验过程进行整体数值模拟，经优化的试件尺寸为表1所列。典型的实验结果已列于表2中，表中v为试件被冲击拉伸的速度，x为试件断裂位置距冲击拉伸端的距离，d为回收试件断口处的平均直径。假设塑性体积应变为零，在断裂处的均匀塑性应变为

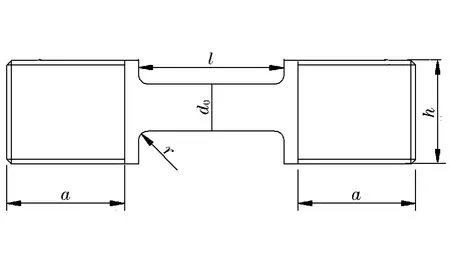
图2 试件示意图Fig.2 The section of the specimens

表1 试件几何尺寸Table 1 The geom etrical parameters of the specimens

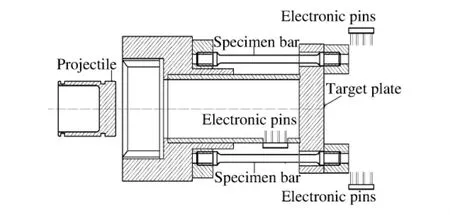
图3 新的高速冲击拉伸实验装置Fig.3 A cross-sectional diagram of the novel facility for high-speed tensile experiments

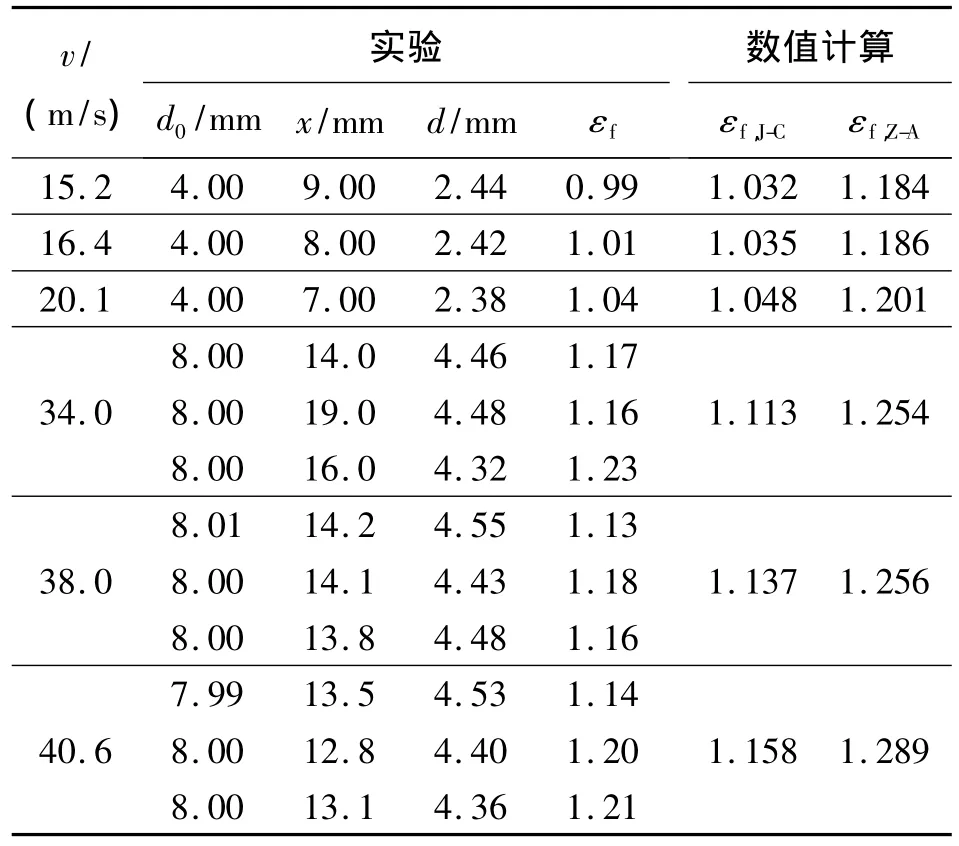
表2 实验及数值计算结果Tab le 2 Experimental data and com puted results

此类拉伸Hopkinson装置所能达到的冲击拉伸速度很有限。为了在更高的冲击拉伸速度下研究OFHC杆的冲击拉伸断裂，陈大年等［5］基于一级气体炮系统，建立了如图3所示的一种新的高速冲击拉伸断裂实验装置(装置B)。这种装置主要由一级气体炮驱动平面飞片和高速飞片击靶牵引多根拉伸试件组成，有3个优点:(1)充分发挥一级气体炮的高速发射能力，可达到很高的冲击拉伸速度;(2)冲击拉伸端的速度可用电探针技术精确测量;(3)同一发实验可采用多根试件，用于分析由于试件材料及加工引起的实验结果的分散性。采用这种装置可以研究试件材料的临界冲击拉伸速度。当冲击拉伸速度达到临界值时，塑性波速趋于零，致使应变集中于冲击拉伸端，断裂也就发生在冲击拉伸端。临界冲击拉伸速度的实验值是由应力波效应、颈缩及损伤演化共同作用的结果。D.S.Clark等［7］指出，为了从实验上取得有效的临界冲击拉伸速度，试件的长径比必须大于13，试件两端的过渡区也有一定的要求。我们采用图3的实验装置对OFHC杆进行高速冲击拉伸实验，试件的几何参数也已列于表1中，典型实验结果列于表2中。由表2可见，当冲击拉伸速度小于34.0 m/s时，颈缩与断裂的位置有随机性，当冲击拉伸速度大于38.0 m/s时，颈缩与断裂总是发生在冲击拉伸端附近，杆的其他部位应变小于0.05。因此，确定此材料的实验临界冲击拉伸速度为40 m/s。由表2可见，试件杆的断裂存在一定的随机性，这是因为试件的拉伸至破坏是受应力波作用的结果，尤其是装置B中，长116 mm的试样在破坏前不可能实现应力应变均匀，不均匀应变状态下的破坏有随机性。此外，试件材料与加工的随机因素也是试件断裂随机性的原因。这正是动态断裂包括临界冲击拉伸速度研究中的难点。由表2可见，OFHC杆的局部化断裂应变εf随冲击拉伸速度的增大并不明显。

2 基于含空穴样本模型的冲击拉伸杆断裂应变

对于准静态拉伸杆断裂，A.R.Ragab［3-4］定义了一种含空穴材料的样本体积单元RVE，如图4所示。在轴对称的颈缩杆中设置有一个空穴，提出一种基于空穴颈缩的断裂模型，并依据一系列材料的无刻槽及有刻槽杆的准静态拉伸断裂实验，已确定了很多合金的特征微力学参数。模型可表达为［3-4］，当

时，空穴聚集，杆件发生断裂。式中:σ1，av为作用于杆上的平均拉伸应力

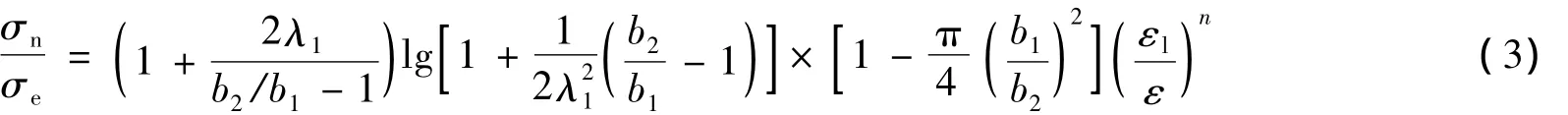
λ1=a1/b1，n为基体材料硬化指数，ε为单元的平均应变，εl为空穴间基体的平均应变

此断裂模型中涉及空穴参数的演化，A.R.Ragab［3－4］采用了很多经验性的方程，有一定的人为性。这里探讨采用由准静态实验确定的典型延性材料的特征微力学参数，采用数值方法研究冲击拉伸杆断裂。

图4 轴对称颈缩杆与含空穴的样本体积单元Fig.4 Axisymmtric necked rod and a representative volume elementwith void

图5 动态计算的单元模型Fig.5 Dynamic computational RVEmodel

用于研究冲击拉伸杆断裂应变的含空穴样本模型如图5所示，初始的特征参数空隙度f0、空穴纵横比W0和单元的纵横比λ0等定义为［8］

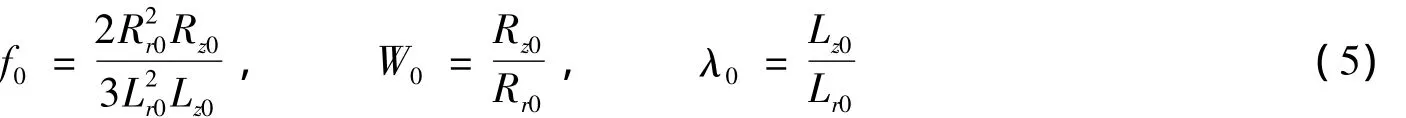
式中:Rr0、Rz0、Lr0、Lz0分别是椭球空穴和单元的半径及半轴长。单元的顶部施加一个沿轴向的冲击拉伸速度，经初始快速上升后，保持一定时间的常速v。应该指出，试件被拉伸至断裂的过程中有应力波作用过程，对于拉伸Hopkinson试件，使试件发生颈缩至断裂的拉伸波有多次作用，比较多次作用与一次作用(拉伸历时一样)的结果，差别不显著。对于装置B，我们只取了平均拉伸速度，与实验的真实拉伸载荷存在一定差异。考虑对称性，对单元的1/4进行计算，随着单元被冲击加载，空隙度f、空穴纵横比W及单元的纵横比λ均随时间而演变。单元宏观平均应变如下表示

主应力Σz及Σr定义为单元边界上平均的单位面积力，采用LS-DYNA程序［5］模拟OFHC中椭球空穴在单轴冲击拉伸下的增长与失稳。应力表达为

式中:q为人为粘性，sij为偏应力。当压力超过Hugoniot弹性极限时，p由Grüneisen状态方程确定

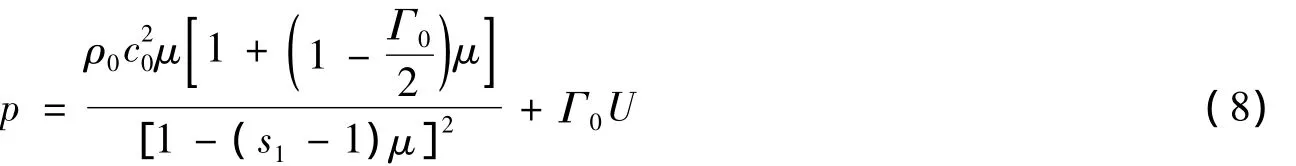
表达基体材料Von Mises等效应力σe的动态本构关系是数值模拟基体中空穴增长与失稳的关键之一。由动态扭转及拉、压Hopkinson实验，已建立了一系列动态本构关系。Johnson-Cook关系为［9］

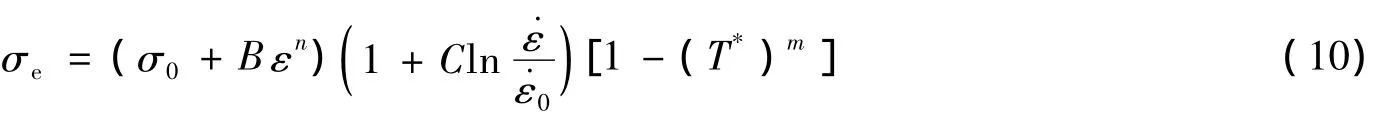
对于 OFHC，σ0=90 MPa，B=292 MPa，n1=0.31，C=0.025，m=1.09。

F.J.Zerilli等［10］基于微结构提出两类本构关系。对于FCC金属，Z-A本构关系为

对于 OFHC，=46.5 MPa=890.0 MPa，=0.002 8 K－1=0.000 115 K－1。

为了检验所建立的这些本构关系能否应用于一般应力状态，G.R.Johnson等［11］分别采用J-C［9］和Z-A［10］本构关系的材料常数，对高导无氧铜进行了Taylor实验(圆柱杆冲击实验)。结论是两种本构关系都较好地符合实验，其中采用Z-A本构关系计算的圆柱体最终形状更符合实验结果。然而，W.K.Rule等［8］指出“由于非均匀应力和应变的存在，采用此试验进行本构关系检验尚存疑义”。事实上，Z-A模型基于位错动力学，分析了典型的FCC和BCC金属的温度和应变率效应。J-C本构关系中的变量设为可分离，是经验性的，缺乏物理基础。D.N.Chen等［12］对OFHC在冲击荷载下的本构关系作了更多的讨论。

对于 OFHC，取纯铜(99.97%)的微力学参数［3-4］，f0=0.002 5，W0=1.6，λ0=0.5。关于空穴失稳的条件，不能从Σz随Er变化曲线的极值点确定，准静态拉伸下杆件发生塑性失稳的条件并不能应用于动态拉伸下杆件的失稳，陈大年等［13］在研究膨胀壳体材料的失稳问题时已指出。如果从空穴形状演化lnW随Er的变化来判定空穴失稳，可以发现，当单元平均径向应变Er在1.1～1.2之间，lnW有突变，而且应变率效应也并非很明显，这些结果与实验结果比较一致。把空穴失稳时的Er与实验测得的局部化断裂应变作比较，列于表2中。由表2可见，采用J-C本构关系计算的Er比较符合实验的平均局部断裂应变εf。就此而言，文献［5］的结论与此结论不一致，这是因为，前者基于文献［3－4］的断裂模型，即方程(2)。而本文此结论基于我们提出的lnW突变判据。两种不同的本构模型，在不同的断裂模型下，可以导出不同的结果。应该指出，杆件的拉伸断裂与平板的层裂从微力学机理上是不一样的，前者主要是空穴形状演化，后者主要是空穴体积演化。典型的数值模拟结果如图6～7所示。

图6 含空穴OFHC样本体积单元的主应力Σz/σ0和空隙度f随Er的变化Fig.6 The variations of the principal stress Σz/σ0 and the porosity f with the strain Er of the RVE with void

图7 含空穴OFHC样本材料体积的空穴形状演化ln W随Er的变化Fig.7 The variations of the aspect ratio of void ln W with the strain Er of the RVE with void

3 基于含空穴样本模型的临界冲击拉伸速度分析

基于上述含空穴样本模型，可以对OFHC的临界冲击拉伸速度实验值进行分析。如果以空穴形状演化lnW随时间t的变化来判定空穴失稳，当lnW达到极大值时作为空穴失稳判据，即微空穴失稳的时刻t*与冲击拉伸速度v有关，如图8所示。使样本材料体积单元发生空穴失稳的时间接近零时的拉伸速度应该对应于临界冲击拉伸速度。拉伸速度与空穴失稳时刻的关系如图9所示，从图9看出，OFHC的临界冲击拉伸速度为40～60 m/s。然而，这种逼近不是很确切，仅是一种探讨。

图8 含空穴OFHC样本体积单元的空穴形状演化ln W随时间的变化Fig.8 The variations of the aspect ratio of void ln W with the time t of the RVE with void

图9 含空穴OFHC样本体积单元的空穴失稳时刻t*随冲击拉伸速度的变化Fig.9 The variations of the time t*for void instability of the RVE with the tensile velocities

4结论

(1)采用拉伸Hopkinson装置及一种基于一级气体炮的高速冲击拉伸断裂装置，研究了无刻槽高导无氧铜杆在一系列冲击拉伸速度下的断裂应变，并得到临界冲击拉伸速度的实验值为40 m/s。实验结果表明，局部化断裂应变随拉伸速度的增大并不明显。

(2)采用一种动态计算的含空穴的样本体积单元模型，研究单轴冲击拉伸下空穴的增长与失稳过程。提出以空穴形状突变为空穴失稳判据，考察了基体动态本构关系对于空穴演化的影响，并把样本体积单元中空穴失稳时的平均径向应变与实验的断裂应变作了比较，采用J-C本构计算的空穴失稳平均径向应变似乎更符合实验的平均断裂应变。此结论与文献［5］的结论不一致，这是由于所用的断裂模型不一致所致。

(3)采用含空穴受冲击拉伸载荷的高导无氧铜样本体积单元，以空穴形状突变为空穴失稳判据，使样本体积单元的空穴失稳时间接近零的冲击拉伸速度，对应于 OFHC的临界冲击拉伸速度为40～60 m/s，与实验结果也可接近。

［1］Pardoen T，Hutchinson JW.An extended model for void growth and coalescence［J］.Journal of the Mechanics and Physics of Solids，2000，48:2467-2512.

［2］Benzerga A A.Mircomechanics of coalescence in ductile fracture［J］.Journal of the Mechanics and Physics of Solids，2002，50:1332-1362.

［3］Ragab A R.Prediction of ductile fracture in axisymmetric tension by void coalescence［J］.International Journal of Fracture，2000，105:391-409.

［4］Ragab A R.A model for ductile fracture based on internal necking of spheroidal voids［J］.Acta Materialia，2004，52:3997-4009.

［5］陈大年，胡金伟，金扬辉，等.高导无氧铜的临界冲击拉伸速度［J］.爆炸与冲击，2009，29(2):113-118.

CHEN Da-nian，HU Jin-wei，JIN Yang-hui，etal.Critical impactvelocity for oxygen-free high-conductivity copper in tension［J］.Explosion and Shock Waves，2009，29(2):113-118.

［6］Hallquist JO.LS-DYNA keywords use’smanual(Version 970)［M］.USA:LSTC，2003.

［7］Clark D S ，Wood D S.The influence of specimen dimension and shape on the results in tension impact testing［J］.Proceedings ASTM，1950，50:577-585.

［8］RuleW K，Jones SE.A revised form from the Johnson-Cook strength model［J］.International Journal of Impact Engineering，1998，21:609-624.

［9］Johnson G R，Cook W H.A constitutivemodel and data formetals subjected to large strains，high strain-rates and high temperatures［C］∥Proceedings of the Seventh International Symposium on Ballistics.The Hague，The Netherlands，1983:541-547.

［10］Zerilli F J，Armstrong R W.Dislocation-mechanics-based constitutive relations for material dynamics calculations［J］.Journal of Applied Physics，1987，61:1816-1825.

［11］Johnson G R，Holmquist T J.Evaluation of cylinder-impact test data for constitutivemodel constants［J］.Journal of Applied Physics，1988，64:3901-3910.

［12］Chen D N，Fan C L，Xie SG，et al.Study on constitutive relations and spallmodels for oxygen-free high-conductivity copper under planar shock tests［J］.Journal of Applied Physics，2007，101:1-9.

［13］陈大年，尹志华.对膨胀壳体材料失稳的一种简化处理［J］.爆炸与冲击，1999，19(3):193-198.

CHEN Da-nian，YIN Zhi-hua.A simplified approach tomaterial instability of expanding shells［J］.Explosion and Shock Waves，1999，19(3):193-198.