含诱导缺陷薄壁圆管耐撞性优化设计*
2011-06-20殷之平李玉龙黄其青
殷之平,李玉龙,黄其青
(西北工业大学航空学院,陕西 西安 710072)
薄壁结构作为低成本、高吸能效率的构件,被广泛应用于飞机、汽车、铁路等几乎所有交通工具的碰撞动能耗散系统中[1-3]。
为了获得稳定的吸能效果,研究者们设计了含诱导缺陷的薄壳结构。诱导结构的主要作用是使结构沿着诱导缺陷,产生稳定的渐进屈曲模式,以最大程度地吸收冲击能量[4]。张涛等[4]研究了薄壁组合结构及其设计缺陷结构的吸能特性,研究显示设定一定的诱导缺陷可以降低撞击过程中的峰值载荷。L.Sunghak等[5]采用数值方法模拟具有诱导矩形孔的方管的塑性变形能,计算表明设计合理的诱导缺陷能提高能量吸收并减小冲击力。G.H.Daneshi等[6]采用理论方法研究具有周期凹槽的圆柱壳结构的动态屈曲,采用理想弹塑性模型假设,将凹槽处看作塑性铰,计算圆柱壳结构的轴向抵抗力,结果与实验较吻合。张雄等[1-2]采用凹坑作为诱导缺陷来提高能量吸收和减小冲击力。
为了获得结构的最大吸能能力,学者们进行了大量的优化方面的研究[7-8],给出了运用各种反应曲面法(RSM方法)技术进行耐撞性优化设计分析,通过该技术,解决了耐撞性仿真分析的计算量大、无法进行大量仿真分析的实际问题,为耐撞性优化设计提供了思路。
本文中,在基本遗传算法的基础上,建立一套改进的基于移动最小二乘法的遗传算法动力学优化算法,设计一种具有诱导缺陷的薄壁圆管吸能结构,运用优化程序,以吸能效率最大化为目标,进行优化分析,给出优化设计结果。
1 基于改进的遗传算法动力学优化设计
遗传算法(Genetic algorithm,GA)是优化算法中常用的一种优化算法,基本操作主要包括初始种群生成、计算种群个体函数值和适应度、遗传操作等,流程如图1所示。
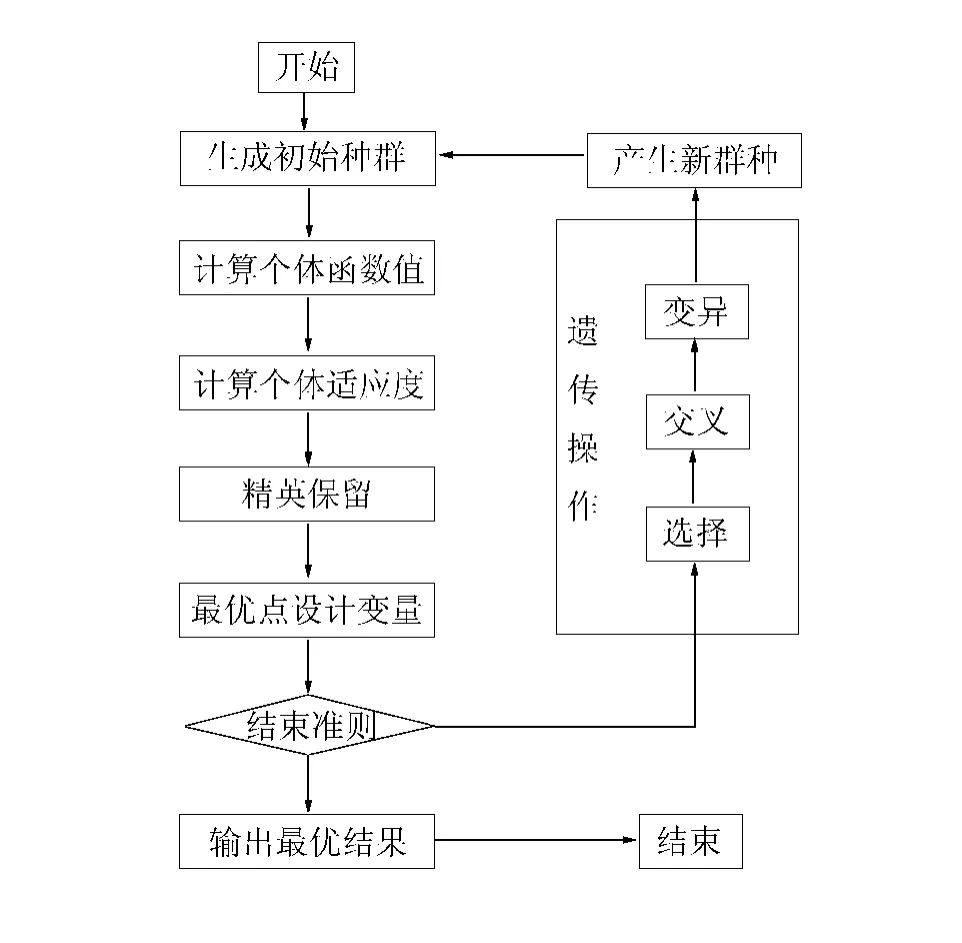
图1 基本遗传算法流程Fig.1 GA optimization method
当优化目标函数为隐式时,通常采用响应曲面拟合技术进行拟合,具有一定拟合精度的为移动最小二乘法(Moving least square,MLS)[9]。本文中采用MLS拟合技术建立结构参数与吸能之间的函数关系。在最优点附近添加一些已知解,可以提高MLS在最优点的拟合精度,因此,可以通过迭代调用 MSC.Patran/Dytran软件进行数值模拟,将分析结果添加到MLS拟合用初始数据中,建立图2所示的改进的基于MLS的遗传算法动力学流程。
2 含诱导缺陷薄壁圆管结构优化分析
结构的吸能效果可以用总体比效率[2]
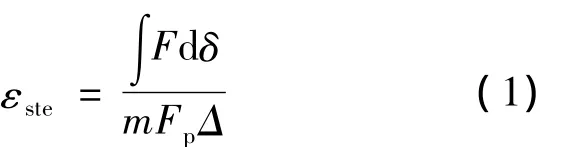
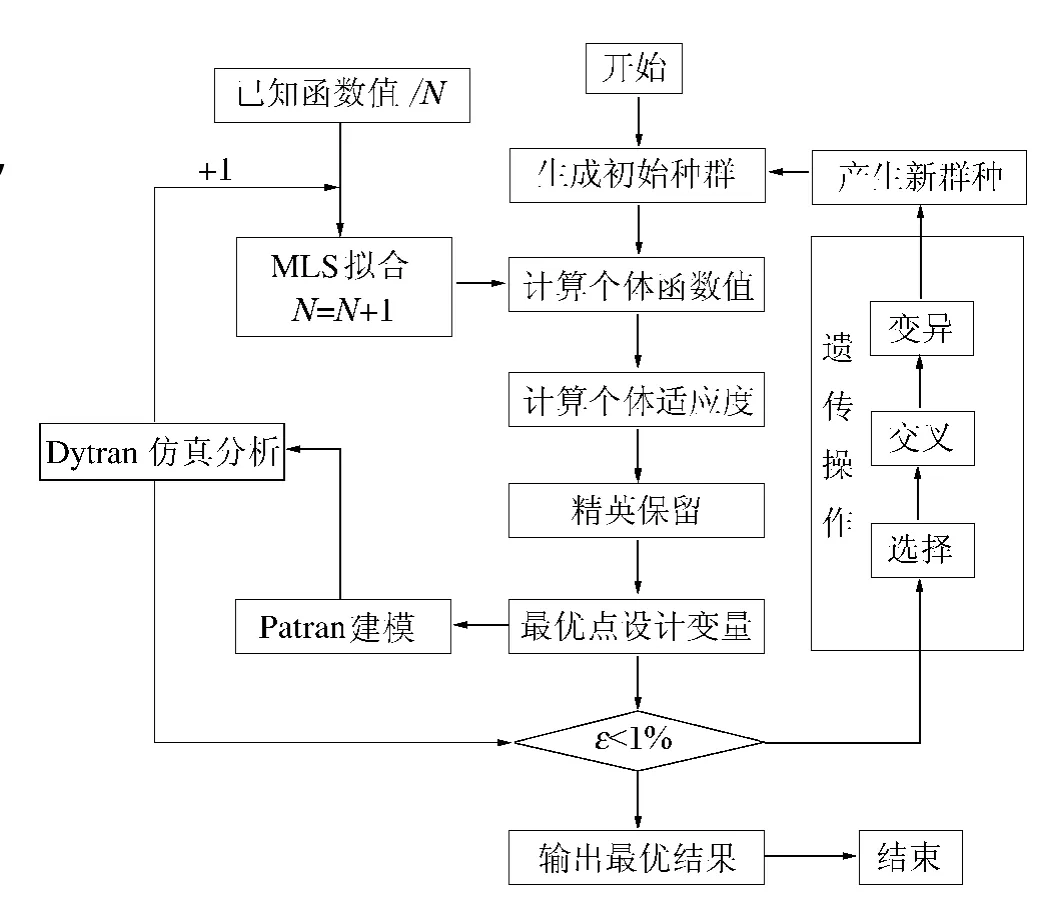
图2 改进的基于MLS的遗传算法优化流程Fig.2 Modified GA optimizationmethod based on MLS
来衡量,式中:F为撞击载荷,δ为撞击变形,∫Fdδ为结构吸收能量,m为结构质量,Fp为撞击过程中峰值载荷,Δ为结构撞击最终变形量。
薄壁圆管结构撞击最大载荷发生在形成最初皱褶变形瞬间,如果设计一个结构,降低最初形成皱褶时的撞击载荷,则可以提升结构的总体吸能效率。为此,在结构中引入初始缺陷,设计出了如图3所示的含缺陷薄壁圆管,下面对该结构进行优化设计研究。
2.1 结构简介
薄壁圆管结构,圆管半径R=20 mm,总长L=180 mm,管壁厚H=1.2 mm,缺陷设定为4个均匀分布的矩形诱导缺陷,缺陷尺寸用长度l和夹角θ来控制,结构简图见图3(a),结构网格见图3(b),撞击质量块m=400 kg,撞击初始速度v0=8 m/s。
结构材料选取1018钢,材料本构关系用双线性随动强化模型,应变率强化采用Cowper-Symonds模型描述
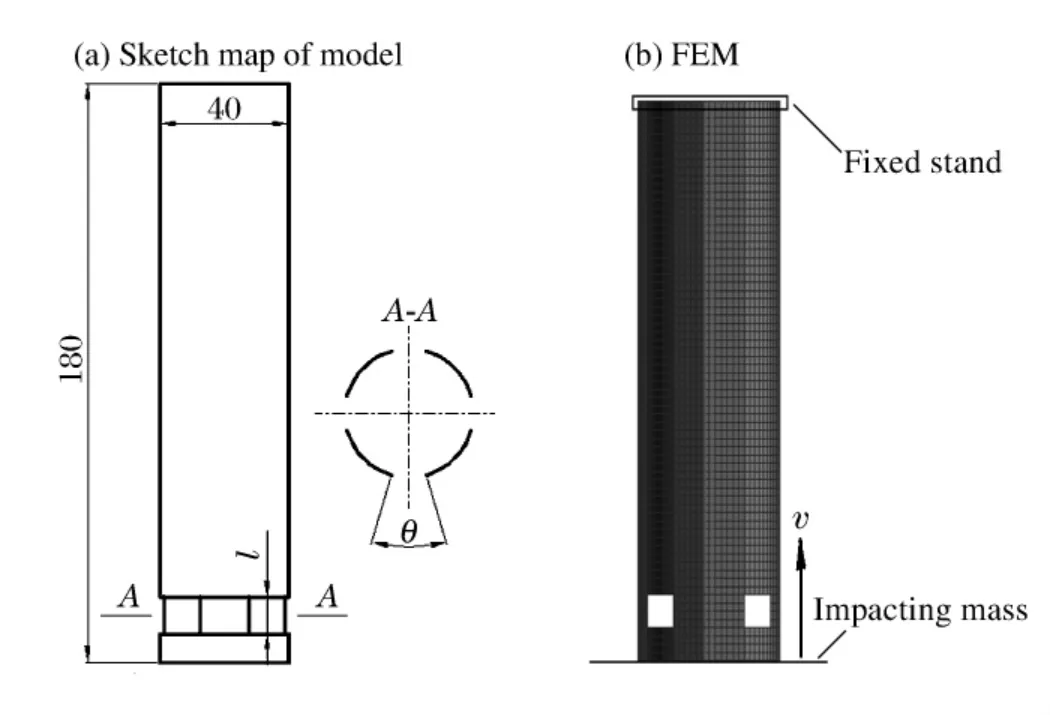
图3 含诱导缺陷薄壁圆管结构Fig.3 Thin-walled circular tubes with triggering holes

式中:σd为动应力,σy为静应力为等效应变率,c和q为材料常数。具体材料常数[2]分别为:弹性模量E=200 GPa,初始屈服应力σ0=310 MPa,硬化模量EH=763 MPa,密度ρ=7.865 t/m3,破坏应变εf=0.75,泊松比 μ =0.27,c=40.0,q=5。
2.2 含诱导缺陷薄壁圆管耐撞性优化分析
优化设计中,设计变量的取值范围为 θ∈[4°,60°],l∈[4 mm,30 mm],设计变量的初始设计空间如表1所示,表中给出了初始设计空间l和θ结构参数时结构撞击吸收能量U和撞击过程中最大撞击载荷Fmax。可以看出,吸收能量与撞击最大载荷之间关系不是线性的,它与载荷变化过程相联系。
运用图2给出的改进的优化设计流程,采用C++语言进行编程,对图3所示的含诱导缺陷的薄壁圆管结构进行动力学优化分析,动力学分析工具为MSC.Patran/Dytran。经过12轮的迭代得到结构设计变量在l≈5.6 mm,θ≈7.5°时,结构撞击载荷最大为59 844 N,结构撞击吸收的总能量为5 138 J,结构质量为0.207 kg,仿真分析的最终变形量为0.140 m,结构耐撞性能参数εste=2.96 kg-1。
分析过程在Intel双核主频2.33 GHz、内存4G的PC机上进行,主网格2.5 mm,单个结构分析30 min,则上述12轮迭代分析需约6 h,分析时间是可以接受的。
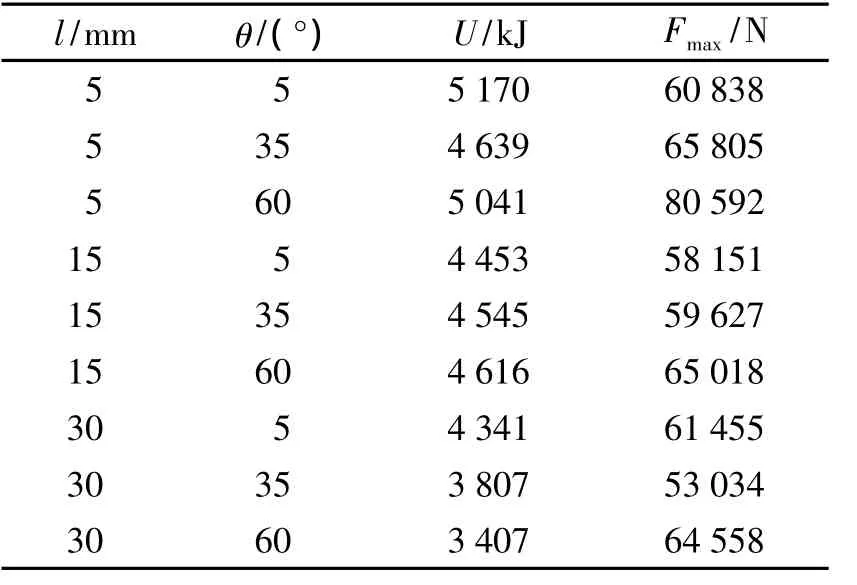
表1 设计变量初始设计空间Table 1 Design parameters and crashing results
2.3 含诱导缺陷优化结构吸能分析
为了方便描述,以下将不含诱导缺陷的结构称为完好结构,含诱导缺陷的优化结构称为优化结构。
优化结构的优化结果:l≈5.6mm,θ≈7.5°,撞击变形云图如图4(a)所示。完好结构的耐撞性变形云图如图4(b)所示,完好结构的最大撞击载荷为62 051 N,最大撞击吸收能量为4 052 J,结构质量为0.213 kg,最大撞击可变形量为0.140 m,则该结构的总体比效率εste=2.19 kg-1。
从结果可以看出,优化结构的吸能效果明显优于完好结构,吸能提高了35%。
完好结构和优化结构的撞击变形模式对比如图5所示,结构的变形模式是一致的,均为典型的非轴对称金刚石模式,即结构的缺陷并没有从根本上改变结构的变形模式。完好结构的变形表现为“三角形”模式,设计了4个缺陷的结构变形表现为“四边形”模式,说明4个诱导缺陷起到诱导作用,促使结构在4个缺陷处形成诱导变形,最终形成了“四边形”的变形形状。
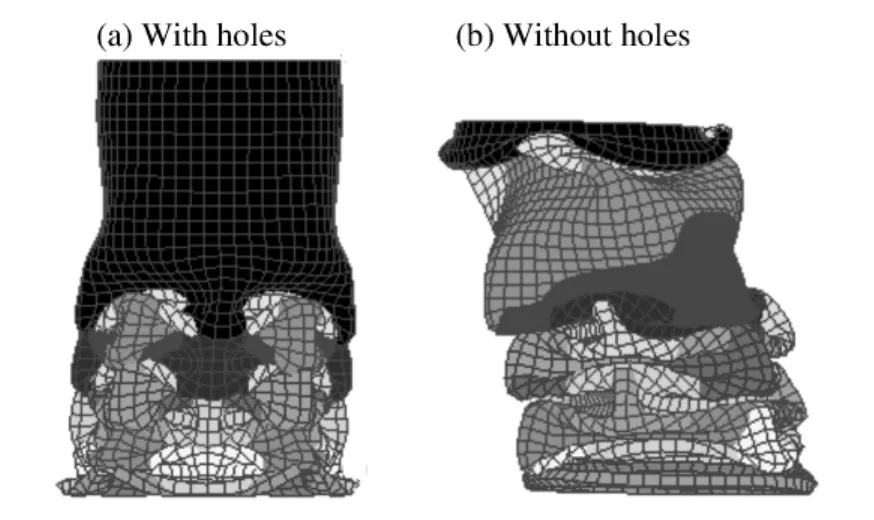
图4 结构耐撞性变形云图Fig.4 Crushing deformations of tubes
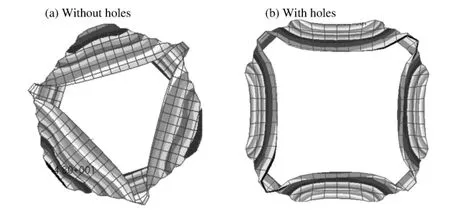
图5 结构变形模式对比Fig.5 Comparison of deformation modes
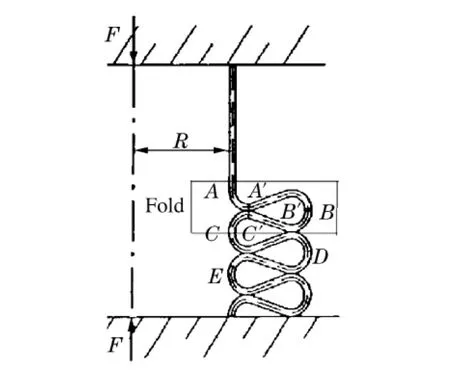
图6 结构变形皱褶示意图Fig.6 Typical deformation of tube
如图6所示,将图中的A-B-C称为一个完整的变形过程,称为皱褶。皱褶形成过程对应于载荷变化曲线如图7所示,即在皱褶形成的过程中载荷经过了2次峰谷值。
各结构撞击载荷变化曲线如图8所示,局部载荷变化曲线如图9所示。在0~4 ms撞击时间内,形成第1个皱褶,结构变形如图10所示,从图中可以看出,优化结构的变形形式表现出与完好结构不同的四边形模式,即优化结构从开始就以稳定的四边形模式进行变形。
完好结构在第1个皱褶形成过程中出现了较大的2次峰值载荷,第1峰值载荷形成皱褶的载荷最大点,之后进入局部失稳变形,载荷降低,之后再变形形成皱褶中的第2个弯折,因而出现第2个峰值载荷。从变形图10(a)看出,结构的变形量较小。
优化结构由于诱导缺陷的设定,使得结构在第1个皱褶形成过程中是一个稳定的变形过程,结构吸能稳定,并且使得平均变形载荷明显高于完好结构的,从变形图10(b)看出,结构的变形量较大。
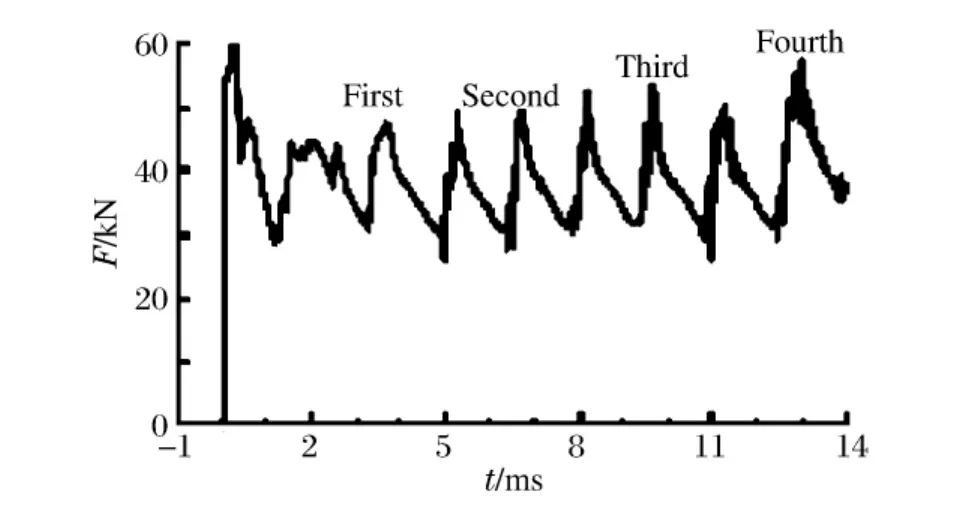
图7 “优化”结构皱褶与载荷变化的关系Fig.7 Axial force-crushing time curve ofmodel with triggering holes
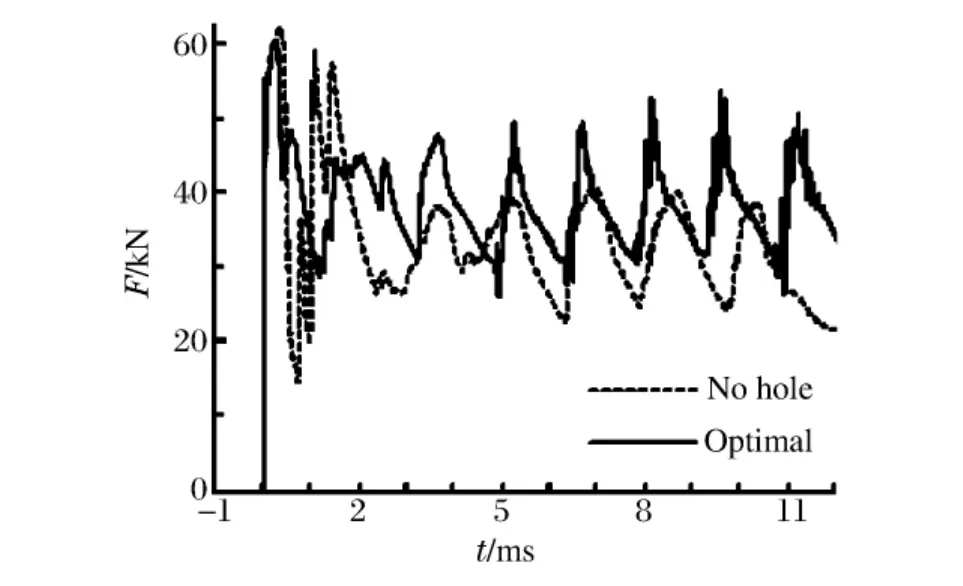
图8 结构撞击载荷变化对比曲线Fig.8 Axial force-crushing curve ofmodel
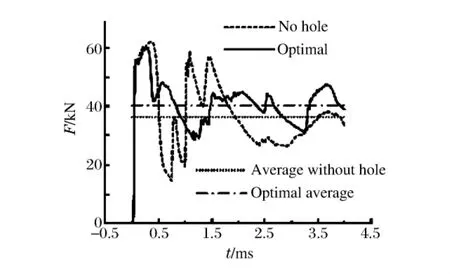
图9 0~4 ms结构撞击载荷变化曲线Fig.9 Axial force-crushing curve within 4 ms
在第2、3皱褶的形成过程中,由于结构变形均为圆管稳定皱褶形成过程,载荷变化表现为峰谷值变化,从图11的4 ms之后的变化曲线可以看出,优化结构载荷的峰谷值为47~32 kN,皱褶长约30 mm;而完好结构的峰谷载荷较低,峰谷值为39~22 kN,皱褶长约35 mm。这说明在结构设计了缺陷后,结构的变形模式由三角形金刚石变形模式转变为四边形金刚石变形模式,结构稳定的皱褶变形形成需要更大的变形载荷,结构的吸能能力更大。能量吸收变化曲线图12显示结构能量吸收的过程即为上述载荷变化关系的体现。
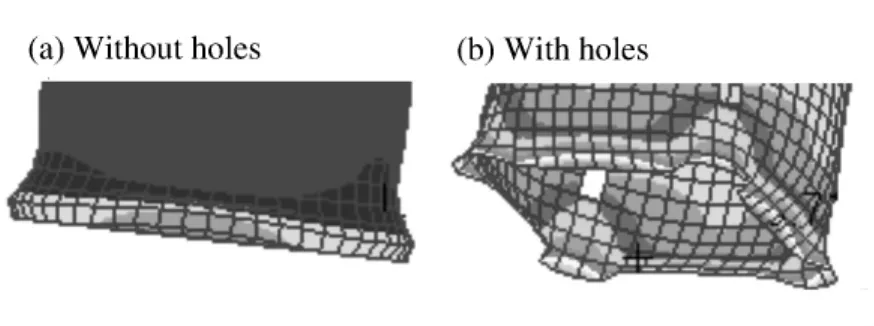
图10 结构第1皱褶变形云图Fig.10 Crushing deformation at the first fold
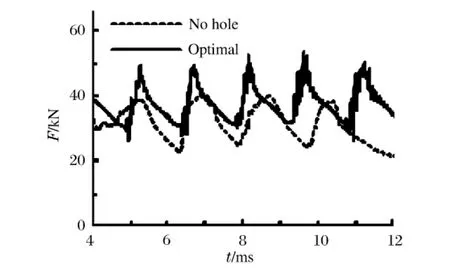
图11 4 ms后的结构撞击载荷变化曲线Fig.11 Axial force-crushing curves after 4 ms
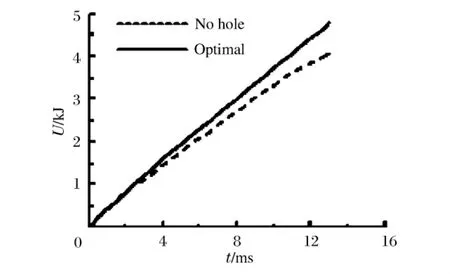
图12 结构撞击吸收能量变化对比曲线Fig.12 Absorbing energy curves
3结论
介绍了结构耐撞性优化设计方法,设计了含诱导缺陷薄壁圆管结构,给出了含诱导缺陷薄壁圆管结构优化设计结果,主要结论如下:(1)薄壁圆管的优化设计显示,建立的结构耐撞性优化设计程序具有一定的通用性,分析流程是可行的,优化结果能反映结构的耐撞性最优特性;(2)设计的含诱导缺陷结构的耐撞性性能优于普通薄壁圆管结构,结构设计简单,便于在结构中使用,而且四边形金刚石变形模式较三角形金刚石变形模式吸能更大;(3)设计的含缺陷薄壁圆管吸能元件结构中,以总体比效率为优化目标时,最优结构参数为l≈5.6 mm,θ≈7.5°。
[1]张巍.轻质薄壁金属结构冲击吸能性与数值研究[D].大连:大连理工大学,2008.
[2]张雄.轻质薄壁结构耐撞性分析与设计优化[D].大连:大连理工大学,2007.
[3]张立玲,高峰.金属薄壁吸能结构耐撞性研究进展[J].机械工人:热加工,2006(1):76-78.
[4]张涛,刘土光,肖汉林,等.高速冲击下薄壁组合结构吸能特性研究[J].爆炸与冲击,2006,26(5):395-403.ZHANG Tao,LIU Tu-guang,XIAO Han-lin,et al.Energy absorption performance of thin-walled structureswith triggering holes subjected to high-speed axial impact[J].Explosion and Shock Waves,2006,26(5):395-403.
[5]Sunghak L,Changsu H,Meungho R,etal.Effectof triggering on the energy absorption capacity of axially compressed aluminum tubes[J].Materials and Design,1999,20(1):31-40.
[6]Daneshi G H,Hosseinipour S J.Elastic plastic theory for initial buckling load of thin-walled grooved tubes under axial compression[J].Journal of Materials Processing Technology,2002,125/126:826-832.
[7]Yamazaki K,Han J.Maximization of the crushing energy absorption of cylindrical shells[J].Advances in Engineering Software,2000,31(6):425-434.
[8]Zarei H R,Kröger M.Multiobjective crashworthiness optimization of circular aluminum tubes[J].Thin-Walled Structures,2006,44(3):301-308.
[9]Krishnamurthy T.Response surface approximation with augmented and compactly supported radial basis functions[C]∥Proceedings of the 44th AIAA/ASME/ASCE/AHS Structures,Structural Dynamics,and Materials Conference.AIAA-2003-1748.Norfolk,Virginia,2003.
