填土和车载对桥墩桩稳定性的影响研究

2011-06-08刘晨彬

铁道勘察 2011年5期

刘晨彬

(铁道第三勘察设计院集团有限公司,天津 300251)

1 概述

桥台的桩基础不仅承受竖向荷载,同时也承受水平荷载、斜向荷载或力矩等,特别是在道路改造中遇到填土(压力差)、汽车荷载(动荷载),直接影响着桥墩桩的稳定性。针对这些复杂的荷载条件,可采用弹性半空间法,将桩顶的竖向荷载和水平荷载分别验算,然后以小变形叠加原理合并其内力和位移，并以修正系数加以修正[1]。然而桩在复杂荷载作用下的受力特征较单一的竖向荷载或水平荷载作用下的受力特征复杂[2～5]。针对复杂荷载条件下的桩的稳定性研究目前主要是采用数值模拟的方法[6～10],该方法能较全面地反映桩的真实受力状态,亦能较好反映桩的稳定性。本文通过极限平衡方法和数值模拟方法,针对桥墩桩在自重、填土和汽车动荷载等条件下剪力和弯矩的研究,分析其对桩稳定性的影响。

2 研究条件

2.1 工程概况

某桥墩桩在建成通车多年后,场地变形基本稳定。因交通改造,需在该桥梁的5号和6号桥墩桩之间填土0.5 m,由于该桥位于软土地基,填土将引起软土压缩沉降,对桥墩桩基产生负摩阻力,从而降低桩基的承载力,影响桩的稳定性。图1为桥墩桩立面,图2为桥墩桩剖面。

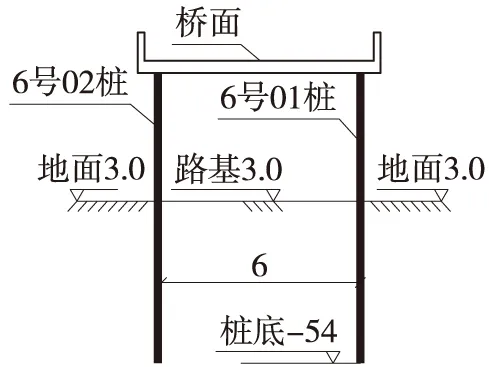
图1 桥墩桩立面(单位：m)

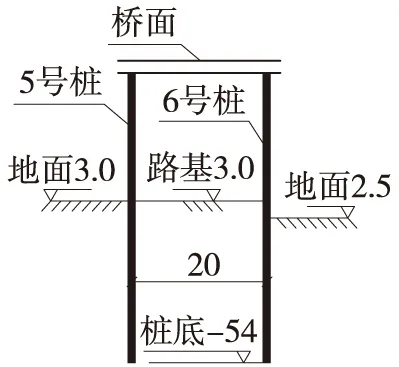
图2 桥墩桩剖面(单位：m)

2.2 荷载条件

桥面荷载传递到桩顶的轴向压力,其计算公式为：桩顶荷载=恒载在桩顶的轴力+活载在桩顶的轴力。该工程中恒载在桩顶的轴力为1 765 kN,活载在桩顶的轴力为1 180 kN,故桩顶荷载为2 945 kN。

3 极限平衡方法

3.1 强度准则

土体采用Mohr-Coulomb强度准则,即土体的强度破坏服从Mohr-Coulomb强度条件,可表示为

τf=σ′tanφ′+c′

式中：τf、σ′分别为破坏面上的剪应力与有效正应力；φ′与c′分别为岩土材科的有效摩擦角与黏聚力。

3.2 压力差

由于存在着土体压力差,桩一端的土体有向另一端运动的趋势,即产生主动土压力；桩另一端的土体有被压缩趋势,即产生被动土压力。因这两种压力的存在,且大小不等,使桩产生了弯矩和剪力,如图3所示。

主动土压力系数计算公式为

Ka=tan2(45°-φ/2)

主动土压力计算公式为

被动土压力系数计算公式为

Kp=tan2(45°+φ/2)

被动土压力计算公式为

式中q——路面荷载；

c——土体内聚力；

φ——内摩擦角；

γ——土体重度。

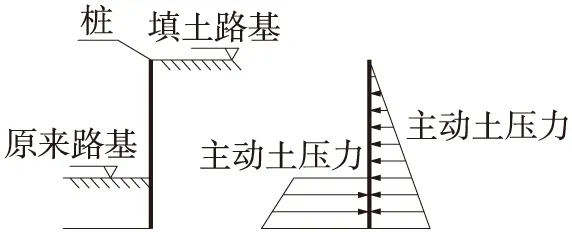
图3 极限平衡法土压力计算示意

3.3 弯矩和剪力

假定桩底部与土体为铰支连接,桩长为x,根据桩前后主、被动土压力受力平衡,有

由上式可求得桩长x,再按结构力学的方法,可求得桩的弯矩和剪力。

3.4 桥墩桩弯矩和剪力分析

6号桩桩前土体(靠近路基一侧)受到路基填土自重压力,产生主动土压； 6号桩桩后土体(靠近地面一侧)受桩挤压影响,产生被动土压力,致使该桥墩桩产生压力差,导致弯矩的产生,最大弯矩出现在距离路面8 m处,其值约为382.5 kN·m,如图4所示。

路基以下土体受路基填土自重压力,土体位移有下沉趋势,在路基土体临界沉降深度范围内,6号桩所受土体摩擦力竖直向下,即6号桩与桩前土体产生负摩阻力,最大剪力出现在距离路面12 m处,其值约为320 kN,如图5所示。

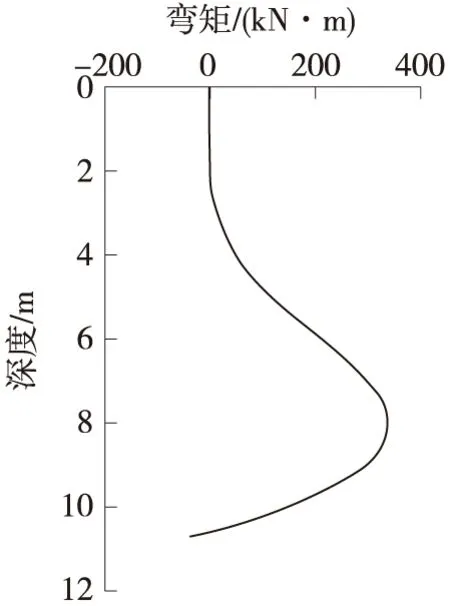
图4 6号弯矩

图5 6号剪力

4 有限元分析

4.1 数值模型

选取6号桩为分析对象,模型长20 m(沿X轴方向),宽6 m(沿Y轴方向),高70 m(沿Z轴方向),土体模型共划分75 166个节点,67 200个单元,桩划分为54段,共55个节点。图6为模型网格,图7为桩土模型。

图6 模型网格(单位：m)

图7 桩土模型(单位：m)

4.2 模拟条件

数值模拟时,土体底部采用固定约束,土体四周采用法向铰支约束,桩底部节点采用铰支方法与土体连接,其他节点直接与土体节点连接,在桩顶施加桥面传递的轴向压力,其值为2 945 kN,桩端5 m长度范围内桩半径为0.4 m,其他部分桩半径为0.6 m。

4.3 物理力学参数

土体的物理力学参数见表1,桩体物理力学参数见表2,桩土相互作用参数见表3

表1 土体物理力学参数

表2 桩体物理力学参数

表3 桩土相互作用参数

4.4 模拟工况

数值模拟过程共分为三个工况,即无填土无汽车荷载的初始状态，有填土荷载无汽车荷载的填土桩土，有填土有汽车荷载的动载状态。模拟中将汽车荷载乘以1.2施加于路面。

4.5 模拟结果分析

图8为三种工况下桥墩桩的弯矩,从图8中可知，在无填土无汽车荷载下,桥墩桩的最大弯矩约为0.01 kN·m,约为0；在填土荷载作用下,其最大弯矩增加到21.6 kN·m；在填土和汽车荷载共同作用下,其最大弯矩显著增加,约为234.6 kN·m,约为填土作用下的10倍,最大弯矩出现在距离地表8 m处。由此可知，汽车荷载对桥墩桩弯矩影响较大。

图8 6号桩弯矩

图9为三种工况下桥墩桩的剪力,从图中可知，在无填土无汽车荷载下,桥墩桩的最大剪力约为4 203 kN；在填土荷载作用下,其最大剪力增加到4 306 kN；在填土和汽车荷载共同作用下,其最大剪力显著增加,约为5 764 kN,最大剪力出现在距离地表26 m处,约为桥墩桩的中心位置。由此可知汽车荷载对桥墩桩剪力影响较大。

图9 6号桩剪力

图10和图11分别为填土和汽车荷载下土体变形位移,从图中可知填土荷载约使地表在桥墩桩处产生了2 mm的变形；汽车荷载约使地表在桥墩桩处产生了5 mm的变形,约为填土荷载下变形量值的2.5倍。

图10 填土状态下位移

4.6 对比分析

由极限平衡法分析可知,桥墩桩的最大剪力约为320 kN,出现在距离地表12 m处；由数值模拟结果可知,桥墩桩在距离地表12 m处剪力在无填土无汽车荷载下约为3 890.8 kN,在填土条件下约为3 939.6 kN,在填土和汽车荷载下约为4 208.7 kN,增加317.9 kN,与极限平衡法得到结果基本一致。

由极限平衡法分析可知,桥墩桩的最大弯矩约为382.5 kN·m,出现在距离地表8 m；由数值模拟结果可知,桥墩桩在填土条件下最大弯矩为21.6 kN·m,在填土和汽车荷载下约为234.6 kN·m,小于极限平衡法得到结果,但最大弯矩产生的位置相同,均为距离地表8 m处。

由对比分析可知,极限平衡法得到的分析结果较数值模拟方法偏安全。