强度折减有限元法分析边坡失稳判据研究

张 兵 李泰兴

(铁道第三勘察设计院集团公司, 天津 300251)

目前,边坡稳定性分析方法主要有极限平衡法、极限分析法以及有限元法。随着计算机技术及有限元理论的发展,近年来,有限元强度折减法被重视起来。与极限平衡法相比,该方法能够考虑土体的应力应变关系,分析边坡破坏的发生及发展过程,尤其是用来分析复杂边坡时具有极限平衡法无法比拟的优势。但限制该方法在边坡稳定性分析中应用的主要原因是对边坡失稳判据没有形成统一的认识,自从1975年Zienkiewice[1]提出了有限元强度折减法的思想以来,国内外不少学者对失稳判据做了大量的研究工作,提出了不少的研究成果,现在常用的三种失稳判据为：数值收敛性判据、特征点位移判据、塑性区判据[2]。本文采用边坡位移矢量角,利用 ANSYS计算模型,以理想弹塑性材料,基于强度折减法,计算边坡的稳定系数。

1 有限元强度折减法的原理

有限元强度折减法的原理就是逐渐改变折减系数来降低边坡的强度参数值,即将C、tanφ同除以同一个折减系数F,得到新的强度参数值C′、tanφ′。再进行有限元计算,直至折减到边坡达到临界状态,发生破坏为止(如图1),此时的折减系数Fs为边坡的稳定系数。

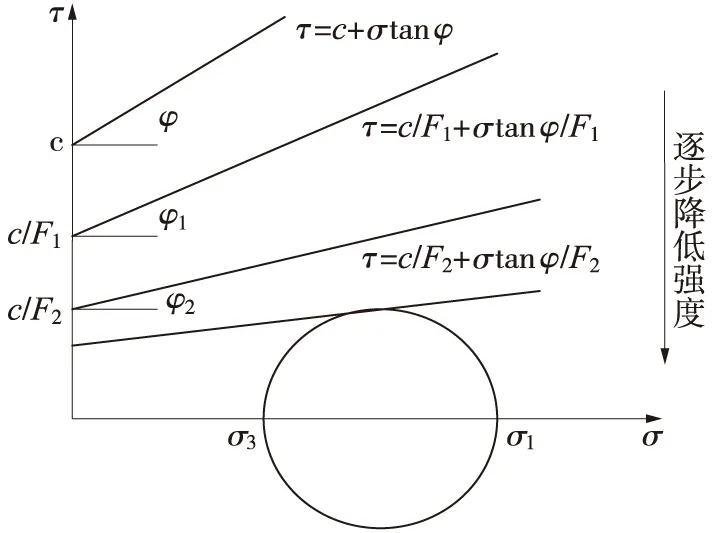
图1 有限元强度折减法示意

2 屈服准则

大型有限元程序ANSYS为岩土体弹塑性分析提供了符合Drucker-Prager屈服条件[3～4]的模型来模拟岩土介质。Drucker-Prager准则是目前岩土工程领域中常用的屈服准则,其表达式为

(1)

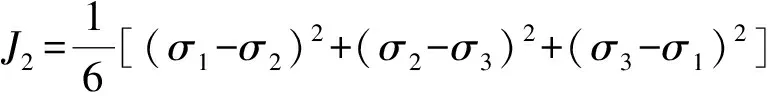
表1为两种屈服准则的转换关系。

表1 D-P1准则与Mohr-Coulomb等面积圆准则的换算关系[5～6]

有

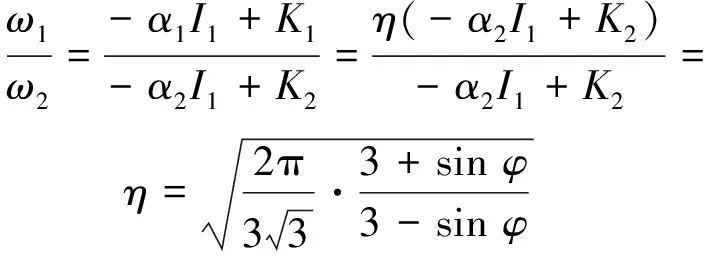
(2)

其中：ω1为D-P1准则稳定系数,ω2为Mohr-Coulomb等面积圆准则稳定系数

3 边坡位移矢量角定义

1995年,贺可强教授、阳吉宝高级工程师在研究堆积层滑坡[7]失稳判据过程中提出来位移矢量角理论[8～10], 边坡位移矢量角就是位移矢量与水平面的夹角,即为垂直位移矢量角。令x(0)、y(0)分别为水平和垂直位移序列,x(1)、y(1)为它们的累加序列

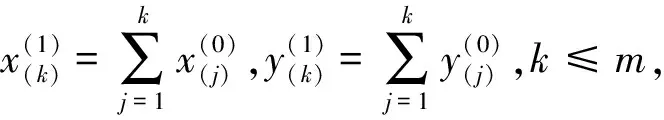
可以看出,在边坡由变形到失稳的发展过程中,随着边坡不同变形演化阶段,位移矢量角有着不同的演化构成规律,这就为利用位移矢量角的变化规律来研究边坡的稳定性提供了可能。

4 边坡实例稳定性分析

选取某铁路H30滑坡,滑坡整体呈马蹄形,滑坡体宽120 m,长约113 m,滑坡后缘高程730 m,前缘高程685 m,相对高差约55 m。滑坡主滑方向27°,整个滑坡体两侧有基岩出露,岩性为云母石英片岩,岩层倾向22°,倾角20°,滑坡体坡向N27°E,坡度25～30°(如图2、表2所示)。

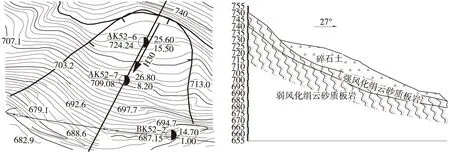
图2 H30滑坡平面及剖面

表2滑坡物理力学参数取值

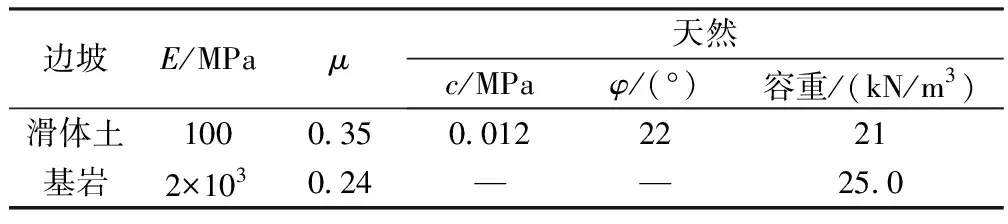
边坡E/MPaμ天然c/MPaφ/(°)容重/(kN/m3)滑体土1000.350.0122221基岩2×1030.24——25.0

计算模型采用8节点(PLANE82)单元划分网络,有限元划分为4661个单元,节点总数为9570,网格划分情况如图3所示。计算区域的底面采用固定约束,左右两侧面均为水平约束约束,其他为自由边界。计算中只考虑岩体自身重力作用。

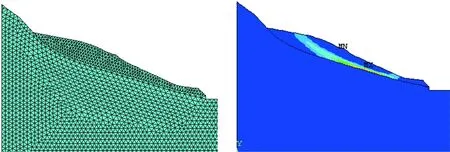
图3 H30滑坡网格划分及塑性变形云图

为了研究边坡位移矢量角的时间、空间特征,从滑坡的后缘、中部、前缘各取两节点作为研究对象,具体上部取8、14节点,中部取236、260节点,下部取202、206节点,根据强度参数的折减,滑坡的位移失量角随着变化(如图4、图5、图6所示)。

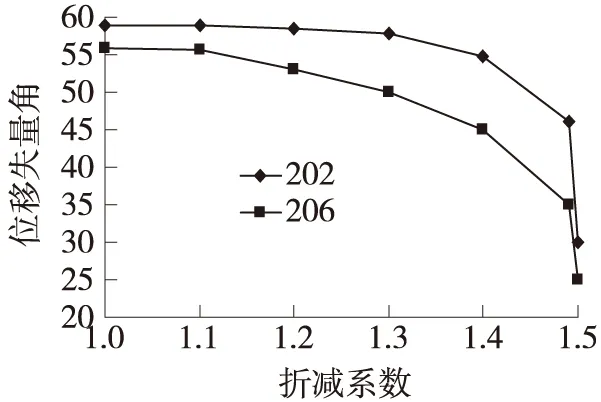
图4 前缘位移矢量角与稳定性关系曲线

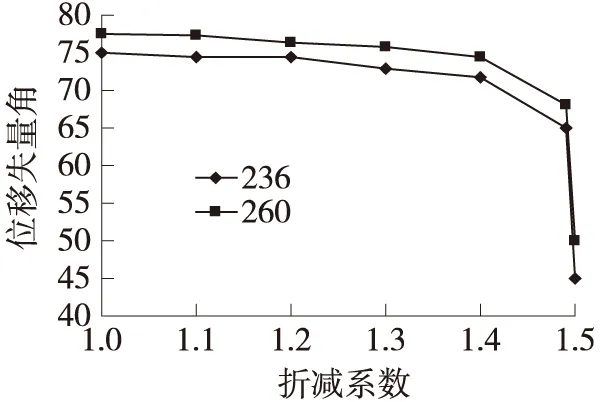
图5 中部位移矢量角与稳定性关系曲线

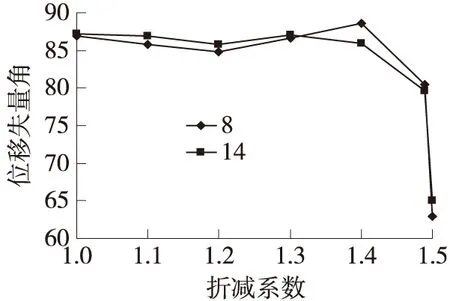
图6 后缘位移矢量角与稳定性关系曲线

纵观边坡表面一系列观测点,位移矢量角随时间的推移,c、φ值的降低,与边坡前缘相比,边坡中部以及后缘的位移矢量角的变化突发性依次减小。无论在哪个位置,越是靠近前缘的点的位移矢量角,在相同的折减系数下,其数值相比较其他点要小,说明越是靠近前缘的点所承受的下滑推力更偏向临空面,这表明位移矢量角能反映各点承受力作用的方向。以上数值模拟分析表明,随着时间的推移,岩土体的风化,滑体物理力学参数的降低,边坡会越来越不稳定,最终发生边坡失稳滑移。将以上的稳定系数按公式(2)换算成在Mohr-Coulomb等面积圆屈服准则下的稳定系数为F=1.242。为了验证有限元建模的正确性,应用工程上常用的极限平衡法分析滑坡的稳定性(如图7)。

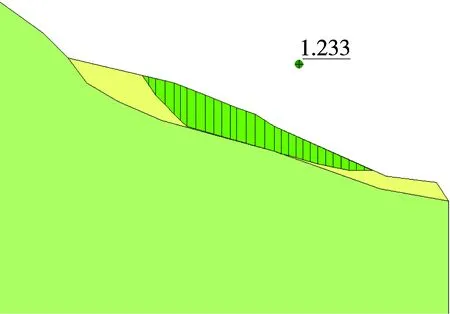
图7 H30滑坡在极限平衡下的稳定性

不同计算方法下的边坡稳定系数如表3所示。

从图3塑性变形云图与图7可以看出，利用两种分析方法计算出的破裂面几乎在同一个位置。从表3中可知,极限平衡法计算得出的稳定系数与基于ANSYS软件的有限元强度折减法下的稳定系数很接近,且其值略大于极限平衡法的计算结果。分析其原因,可认为有限元强度折减法更好的发挥了岩土介质的弹塑性变形所致,其计算结果更符合实际更趋于合理。

表3 不同计算方法下的边坡稳定系数

5 结论

(1)有限元强度折减法能够考虑土体的应力应变关系,分析边坡破坏的发生及发展过程,尤其是用来分析复杂边坡时具有极限平衡法无法比拟的优势,对实际土体开挖和边坡支护具有指导意义。

(2)强度折减法应用于边坡稳定分析中目前的难点是判据问题。通过ANSYS有限元软件与强度折减法相结合,提出了位移矢量角与边坡稳定性的关系,确定边坡稳定系数。通过ANSYS算出的边坡的安全定系数和GEO-SLOPE算出的结果相近,说明该方法在分析边坡稳定性是合理和适用的。

(3)极限平衡法计算得出的稳定系数与有限元强度折减法下的稳定系数很接近,且其值略大于极限平衡法的计算结果，可认为有限元强度折减法更好的发挥了岩土介质的弹塑性变形所致,其计算结果更符合实际更趋于合理。

[1]Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique, 1975,25(4):671-689

[2]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):58-61.

[3]许 靖.建议一种有关岩土力学的屈服准则及其工程应用[D].南宁：广西大学,2005

[4]时卫民,郑颖人.摩尔-库仑屈服准则的等效变换及其在边坡分析中的应用[J].岩土工程技术,2003,1(3):155-159

[5]宗全兵,徐卫亚,孟国涛. D_P准则的性能评估及其在强度折减分析中的适用性研究[J].河海大学学报,2006,26(3):310-315

[6]张 健,范媛媛,黄质宏.ANASYS在边坡稳定分析中的应用[J].贵州工业大学学报,2008，5(5):169-172

[7]王恭先.滑坡学与滑坡防治技术[M].北京：中国铁道出版社,2003

[8]贺可强,阳吉宝，等.堆积层滑坡预测预报及其防治[M].北京：地震出版社,1996

[9]贺可强,阳吉宝，等.堆积层边坡位移矢量角的形成作用机制及其与稳定性演化关系的研究[J].岩石力学与工程学报,2002,21(2)：185-192

[10]贺可强,阳吉宝，等.堆积层边坡表层位移矢量角及其在稳定性预测中的作用与意义[J].岩石力学与工程学报,2003,22(12)：1976-1983