基于梁格法的某斜交变宽连续箱梁桥荷载试验分析
2011-06-08勾风山胡朝辉
勾风山 胡朝辉
(1.广州广大工程检测咨询有限公司, 广东广州 510006; 2.广州诚安路桥检测有限公司, 广东广州 510420)
随着我国交通运输业的蓬勃发展,高速公路、城市立交及高架桥与日俱增,对线路的线形及走向的要求也不断提高,斜、弯箱梁桥不仅能方便地适应复杂线路的线形及宽度变化,且具有整体性能好、抗扭刚度大、弯曲应力图形合理[1]等众多优良的截面特性,因而在桥梁结构中得到了广泛的应用。此类桥梁一般结构形式复杂,需考虑空间受力特性,且不同形式的斜、弯桥又各自具有不同的特点,给结构分析及设计带来一定难度。采用传统的平面杆系单梁法计算,有可能产生较大误差,而板壳和实体单元法虽可分析桥梁结构的各种受力行为,但计算代价高,模型建立复杂。相比之下,梁格法[2]是一种能较好地模拟原结构的分析方法,它具有基本概念清晰、易于理解和使用、计算代价较低等特点。本文以一座斜交变宽连续箱梁桥的结构分析为例,介绍梁格模型的建立,同时基于模型分析结果指导该桥的现场荷载试验,并据此评价该桥的工作性能。
1 工程概况
某桥位于广州市新光快速路猎德大桥主桥南侧,分东、西两幅桥,桥梁全长157.14 m,上部结构为六跨预应力混凝土斜交变宽连续箱梁桥,桥梁跨径组合为(27.25+27+36+22.5×2+21.8) m,单幅桥横向布置为1.0 m(防撞墙)+16.08~21.92 m(变宽三车道)+1.0 m(分隔带)。其中9号~12号跨为斜交异形连续梁,斜交角21°,12号~13号桥跨为斜交连续梁,斜交角为20.5°。横断面9号~10号跨为单箱三室,10号~11号跨由单箱三室变化为单箱四室,11号~15号跨为单箱四室,梁高为1.6~1.8 m。该桥设计活载等级为城-A级汽车荷载,平面布置如图1。
2 有限元模型分析
2.1 梁格模型建立
梁格法的核心思想是利用等效的纵、横梁格代替桥梁上部结构,将分散在板、梁每一区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内。针对该桥的结构特点,对其进行梁格等效简化。
(1)纵梁
纵向梁格位置应与原结构腹板重合,为了加载方便,可在悬臂端部设置虚拟的纵向构件。将箱梁划分为5片纵向梁格,忽略由于截面分割带来的形心位置与腹板中线的偏差。为了保证计算精度,纵向梁格间距取1 m,各纵梁截面中性轴与整体截面中性轴保持一致,以保证箱梁在纵向弯曲时符合平截面假定。
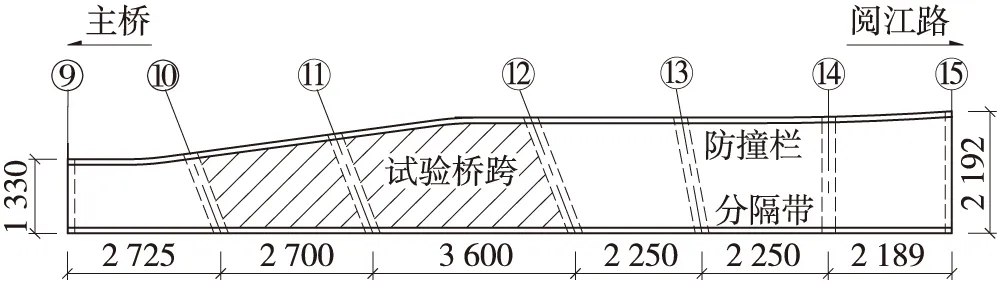
图1 桥梁平面布置(单位:cm)
(2)横梁
横梁分为刚性梁与虚拟梁,虚拟梁可采用工字形梁,顶底板分别取箱梁上下翼板厚度,腹板厚度取很小的值,以达到对横向联系梁的模拟,对于跨中及墩顶部位的横隔板,则采用刚性横梁模拟。
(3)桥面铺装
在梁格模型上建立辅助的板单元,板厚则依据考虑桥面铺装与箱梁材质、边界及联结强度的异同来选取,也可将箱梁顶板适当加厚,在各跨箱梁支承附近、内力变化较大的地方,应进行梁格加密。
基于梁格划分原则,采用Midas/Civil2006通用有限元分析软件建立了该桥空间梁格计算模型,模型共建立1 752个节点,3 219个空间梁单元,梁格划分形式及有限元模型如图2所示。
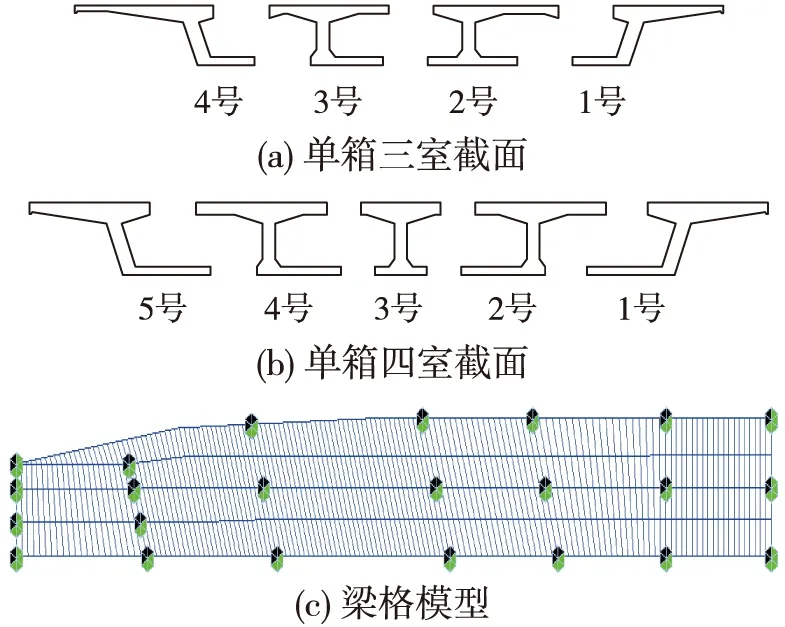
图2 梁格划分形式及有限元模型
2.2 截面特性计算
(1)纵向梁格刚度
抗弯刚度:EIy=E×(纵向梁单元相对箱梁整体截面中性轴的惯性矩)
剪切刚度:腹板内的剪力流由弯曲剪力流和扭转剪力流组成,由于剪力流使腹板产生剪切变形,因此纵向梁格的剪切面积按对应工字梁腹板的横截面积计算。
扭转刚度:GJx=G×(梁格构件顶、底板翼缘对中性轴的惯性矩)
即截面单位宽度内的扭转刚度为
(2)横向梁格刚度
每单位宽度内的抗弯刚度
每单位宽度内的扭转刚度
等效剪切刚度
式中:dw、a、h分别为腹板厚度及箱梁格室宽度、高度,若箱梁内有横隔板,则As还应包括横隔板面积。
3 荷载试验
3.1 试验依据
本次荷载试验主要参照交通部《大跨径混凝土桥梁的试验方法》(简称“方法”);《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62—2004);《公路桥涵施工技术规范》(JTJ041—2000);工程竣工图、变更图及其他相关文件数据。
3.2 测点布置及加载工况
根据“方法”的建议,结合设计资料及现场实际情况,选取10号~12号两孔连续箱梁为荷载试验检测对象,主要测试内容为:试验桥跨控制截面静挠度、静应变、支座沉降、固有频率、阻尼比。
(1)测点布置
挠度测点布置于试验桥跨支点、四分点、跨中位置,其中纵桥向布置9个测点,各跨跨中横向布置3个测点,测点采用长2 cm 特制螺栓固定在桥面铺装层上,竖向变形测量采用二等水准测量,后视点设置在测试桥跨外。
应变测试采用基康钢弦应变计,测试截面为10号~11号桥跨跨中A-A截面、11号支座B-B截面、11号~12号桥跨跨中C-C截面,各截面均布置8个应变测点。
动态测试的测点布置在试验桥跨的跨中、L/4、3L/4位置处,振动信号采用加速度传感器予以量测。
(2)加载工况
为了获得结构试验荷载与变位关系的连续性和防止结构意外损伤[3],加载方式为单次逐级递加到最大荷载,然后一次卸到零级荷载,加载位置与加载工况确定的主要依据是尽可能用最少的加载重车满足试验荷载效率。静载试验采用5台重约35 t的加载车,分5个工况,分别可使10号~11号跨跨中正弯矩、11号支点负弯矩、11号~12号跨跨中正弯矩达到加载效率。加载载位如图3所示,动载试验测试工况包括脉动试验及跳车试验。
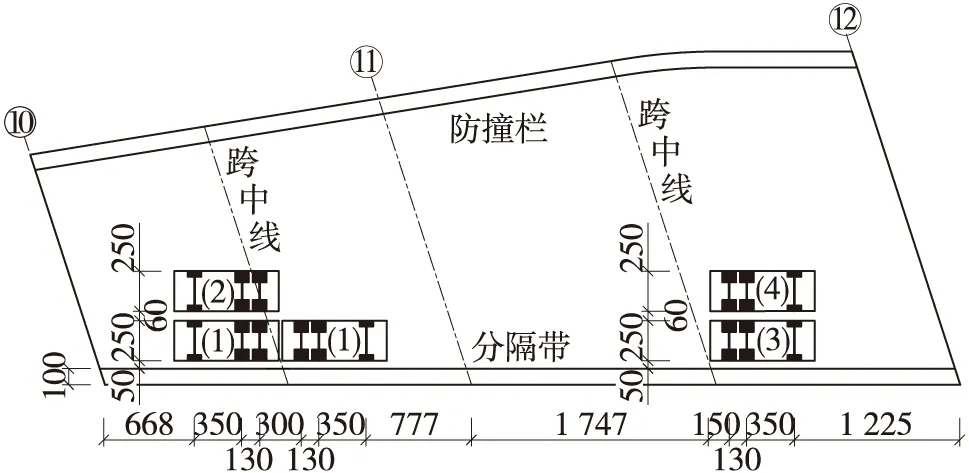
图3 试验加载
3.3 试验结果分析
(1)静载试验结果
最大试验工况下各跨挠度及应变测点的实测值与理论值见表1、表2所示,可见,挠度校验系数在0.50~0.63之间,应变校验系数在0.53~0.62之间,均满足“方法”中关于预应力混凝土桥梁变形测试的要求。实测变形数据小于理论计算值,表明该桥的实际刚度较理论值大,具有一定的承载潜力。试验桥跨跨中3号、7号挠度测点在工况1~5试验荷载作用下实测挠度与荷载关系曲线如图4所示,线性相关系数R分别为0.999 6,0.998 1,表明实测挠度与荷载加载效率成线性关系,箱梁处于弹性工作状态。
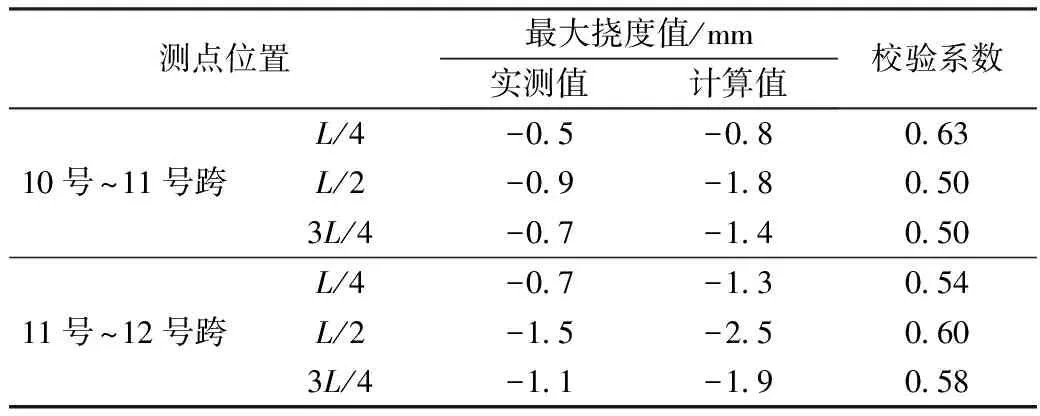
表1 最大试验工况下挠度实测值与理论值

表2 最大试验工况下应变实测值与理论值
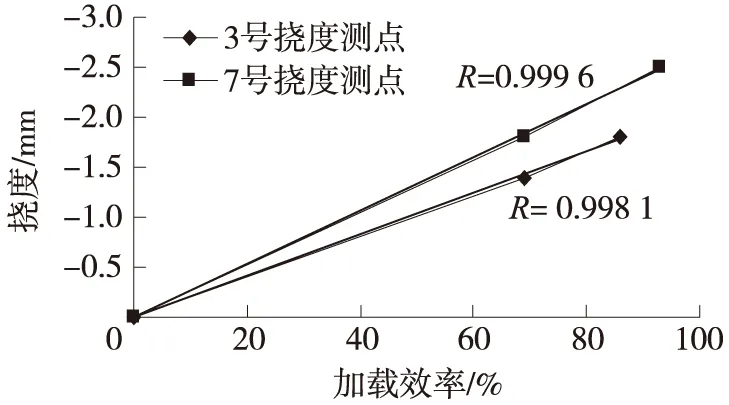
图4 实测挠度值与荷载加载效率关系曲线
试验结束前对试验桥跨进行了残余变形观测,10号~11号跨跨中最大挠度值为-1.7 mm,相应的残余挠度值为0.10 mm,残余挠度与最大挠度的比值为0.06,11号~12号桥跨跨中C-C截面应变测点最大应变值为20 με,相应的残余应变值为2 με,残余应变与最大实测应变的比值为0.10。检测桥跨的残余变形值均满足“方法”中关于预应力混凝土桥梁的要求,即Sp/Stot≤0.20,表明结构处于弹性工作状态。
(2)动载试验结果
试验桥跨动载试验结果见表3。
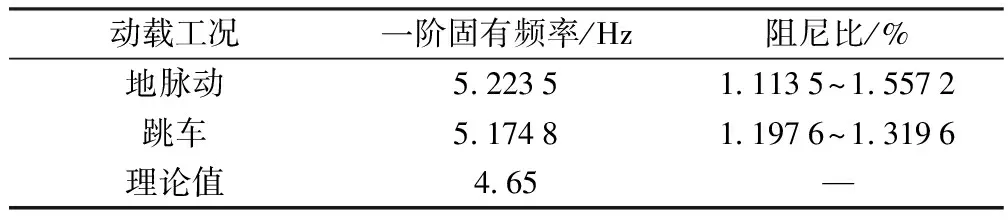
表3 试验跨实测频率及阻尼比
可见,该桥的实测一阶自振频率在5.174 8~5.223 5 Hz之间,阻尼比在1.113 5%~1.557 2%之间,而对应的理论一阶频率为4.65 Hz,实测频率大于理论计算值,说明该桥的实际整体刚度较大,振动响应较小,行车性能良好。
4 结论
基于梁格法的理论分析结果,结合该桥荷载试验的实测数据,可以得出如下结论:
(1)该桥在试验荷载作用下,结构处于弹性工作状态,强度及刚度均能达到设计要求,具有一定的承载潜力。
(2)实测数据与理论值变化趋势较一致,表明本文的梁格模型在纵横梁刚度取值上是合理的,与传统的梁单元法相比,梁格法能较好的反映多室箱梁结构的受力特点,值得在工程应用中推广。
(3)对于此类箱梁桥梁格划分,应据其结构特点对纵横梁的抗弯、抗剪、抗扭刚度进行修正,以保证其刚度与切分前等效。
(4)与板壳、实体单元相比,梁格模型建模方便,计算量小,后处理中能够直接提取结构内力,但前期的截面特性计算量大,对横梁刚度的计算亦无规范的办法,即难以实现梁格的“完全等效”。
[1]V.克里斯特克[捷].何福照,吴德心,译.箱梁理论[M].北京:人民交通出版社,1988
[2]E.C.汉勃利[英].郭文辉,译.桥梁上部构造性能[M].北京:人民交通出版社,1982
[3]张俊平.桥梁检测[M].北京:人民交通出版社,2002
[4]交通部科学研究所.大跨径混凝土桥梁的试验方法(试行)[Z].北京:交通部科学研究所,2001
[5]邵旭东.桥梁工程[M].北京:人民交通出版社,2007
