滑行艇升沉纵摇运动的二维数值预报
2011-06-07晋文菊王志东李力军
晋文菊 王志东 李力军 杨 爽
江苏科技大学船舶与海洋工程学院,江苏镇江 212003
滑行艇升沉纵摇运动的二维数值预报
晋文菊 王志东 李力军 杨 爽
江苏科技大学船舶与海洋工程学院,江苏镇江 212003
基于CFD软件对滑行艇二维简化模型在均匀来流中的运动响应进行数值分析。根据滑行艇的流体动力数值计算结果实时求解滑行艇的运动响应特性,对4种不同傅汝德数下滑行艇的纵摇与垂荡耦合运动特性进行研究,得到艇体升沉幅值、纵摇角随时间的变化特性,以及阻力、升力和力矩随傅汝德数的变化规律,并分析了艇体达到稳定状态所需时间和滑行过程中艇底动压力的变化特性。研究表明:傅汝德数1.5时达到稳定滑行状态的时间仅为80 s;除了在傅汝德数2.0时发生严重振荡,其余3种情况下滑行艇均能够趋于一种“动平衡”状态。
CFD;滑行艇;垂荡;纵摇
1 引言
高速艇的基本特点在于由高速的纵向流动引发的动升力 (矩),艇体升沉纵摇运动中动升力(矩)的作用不可忽视。近年来CFD技术在船舶与海洋工程领域得到了广泛的应用,利用数值计算方法实时计算船舶水动力及其运动响应的工作取得了显著的进展。其中Sato[1]等利用密度函数法并结合液面追踪技术计算了Wigley船体与60系列船模在规则波中的运动;Weymouth[2]等利用液面追踪法对Wigley船体在规则波中的纵摇升沉运动进行数值模拟,并与实验值相比较均取得较为一致的结论;国内张怀新等[3]也对系列60船模周围粘性流场进行初步研究,计算结果合理地反映了船舶实际航行的情况;王兆立等[4]利用CFD软件Fluent模拟滑行艇试验模型在静水面纵向直航时的流场情况,对其水动力性能进行数值计算,与船模试验结果进行了比较,认为此方法在计算滑行艇阻力方面具有可行性及一定的精度,同时能够比较真实地模拟出船舶尾流场。
因此,本文也利用CFD软件编写升沉纵摇耦合运动预报用户自定义程序,并采用预测/修正法求解运动方程,对4种不同体积傅汝得数FV=0.5、1.0、1.5、2.0 条件下滑行艇的纵摇与垂荡耦合运动特性进行研究。
2 计算模型
2.1 计算模型与网格划分
参照美国“斯巴达侦察兵”水面无人艇建立滑行艇二维简化计算模型。“斯巴达侦察兵”是一种高速水面无人快艇,以刚性平底充气艇作为基座,可加装多种“即插即用”型任务模块,如图1a所示。计算模型的网格划分采用分区混合网格系统,并在艇体附近进行了网格加密,其中艇体附近的圆形区域和方形网格区域分别用于保证艇体作纵摇及升沉运动时的网格质量。图1b为计算模型及网格划分示意图,其中上部分为空气域,下部分为水域。计算区域为10L×8L,L为艇长。计算区域底部为固壁无滑移边界条件,左边界与上边界为速度进口,右边界为压力出口。滑行艇简化模型的主要参数见表1。

图1 无人艇模型及网格划分Fig.1 Unmanned surface vessel model and grid partition
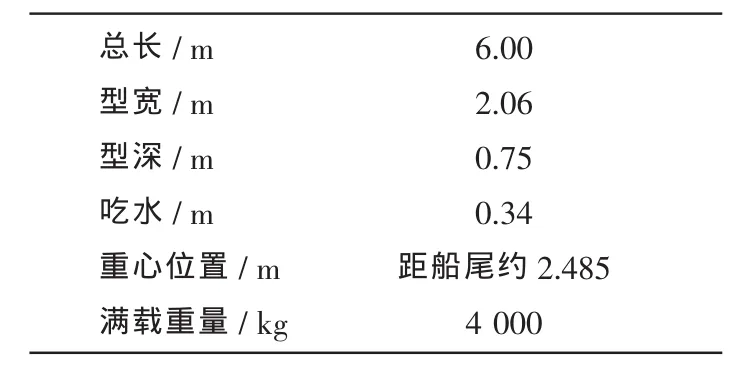
表1 滑行艇主要尺度Tab.1 P rincipal dimensions of p lanning boat
2.2 数值计算方法
本文采用二维非定常分离隐式求解器;利用VOF方法追踪自由液面;自由面重构格式采用Geo-Reconstruct格式;选用k-ε湍流模型;控制方程的扩散项采用中心差分格式离散;对流项采用二阶迎风格式;压力方程采用Body ForceWeighted格式;压力速度耦合求解采用PISO算法。
2.3 滑行艇响应运动预报算法
不计滑行艇的横荡、艏摇及横摇,在原3自由度运动方程的基础上添加人工阻尼项,得到滑行艇的升沉纵摇运动方程如下[5]:
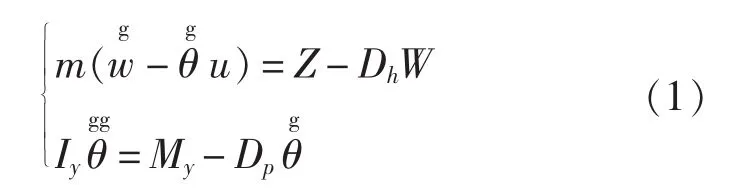
式中,m为艇体的质量,kg;w为艇体垂向速度,m/s;u为艇体前进速度,m/s;Z 为艇体垂向合力,N;θ为艇体纵摇角,rad;My为艇体纵摇力矩;Iy为艇体对y轴的纵摇转动惯量;Dh为垂荡人工阻尼系数,取值 0.1;Dp为纵摇人工阻尼系数,取值 0.1。
在六自由度方程中,若给定任意自由度则可以预测出剩余自由度,例如船舶操纵性的平动实验就是将纵荡、横荡、艏摇运动赋予船体,然后允许船体进行自由纵摇、垂荡与横摇运动,以预测出船体在这三自由度下的速度及角度,反之亦然。同理,式(1)也是在给定速度后(即给定纵荡运动,推进运动是纵荡运动的一种特殊形式),便可预测艇的纵摇与垂荡运动。
采用预测/修正的隐式方法求解运动方程,即通过求解艇的运动方程预测运动速度及角速度,然后采用三阶迎风格式进行修正。

判断结果是否收敛。若收敛则将艇体运动赋给网格[6],滑行艇响应预报算法流程如图2所示。


图2 滑行艇响应预报算法流程图Fig.2 Flowchart for the response prediction of the p lanning b oat
3 计算结果与分析
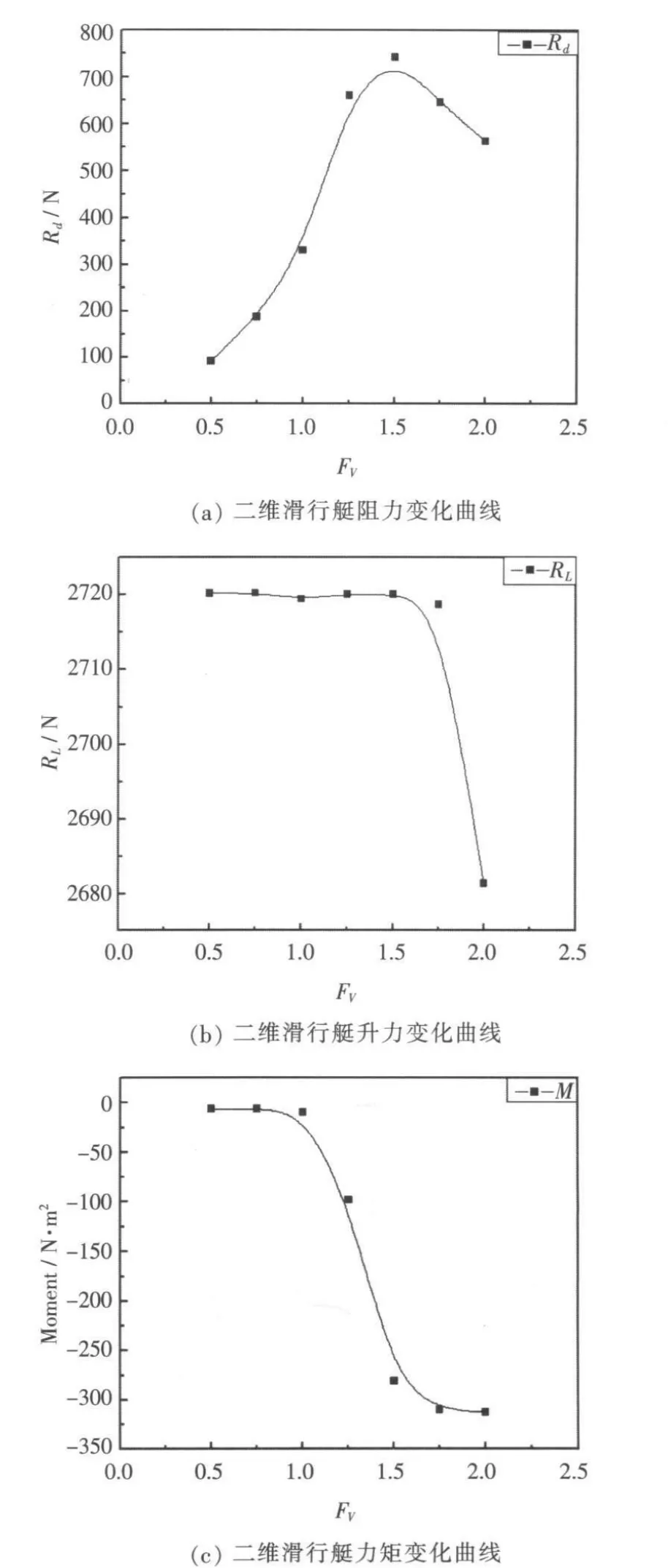
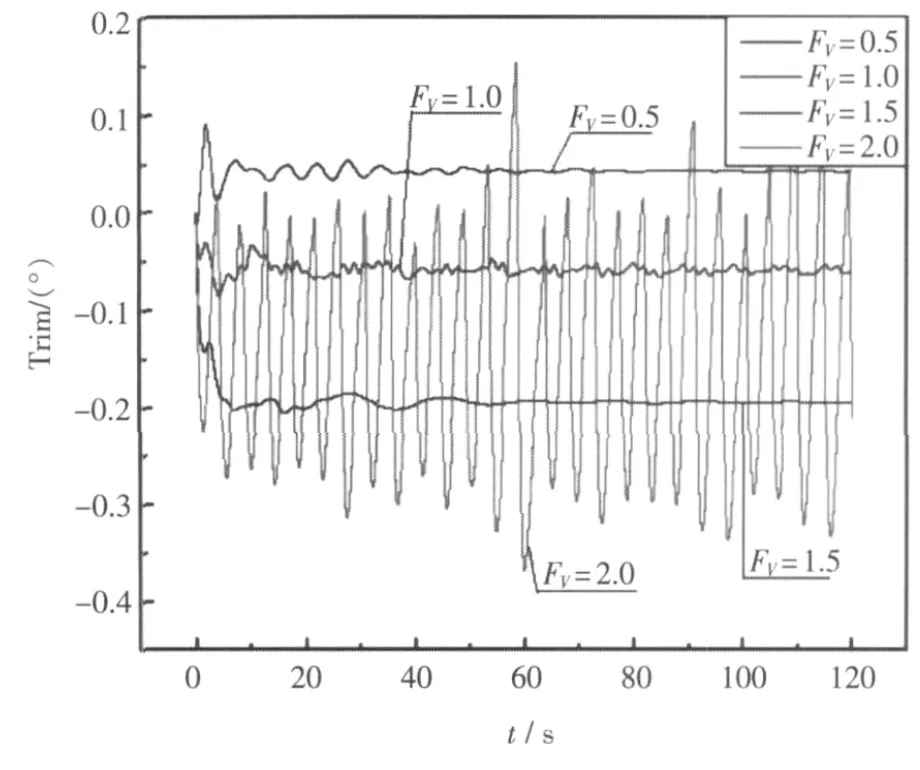
从水动力学的观点出发,若船舶的体积傅汝德数FV≥1则属于高速船,其中包括高速排水型船舶和流体动力增升型船舶。对于1.0 为了分析不同速度下滑行艇的水动力性能,分别计算了 FV为 0.5、1、1.5、2 时的滑行工况。 图3中给出了滑行艇在不同FV数下的阻力、升力及力矩变化曲线。 由图3a可以看出,当 FV≤1.5时,阻力随 FV的增大而增大,随后阻力开始减小。因为在傅汝德数FV=1.5时,滑行艇已进入半滑行状态;当FV=2时滑行艇已进入滑行阶段,所以阻力变小。 由图3b看出滑行艇的升力变化从FV=1.5到FV=2陡然下降。究其原因,主要由于滑行艇在未进入滑行状态前,滑行艇的升力主要靠静浮力来提供。FV=1.5时,滑行艇艇首已抬出水面,艇体重心升高,排水体积减小,静浮力下降,升力已有轻微减小;滑行艇在FV=2时已视作进入滑行状态,在此速度下滑行艇已基本脱离水面。主要由于三维的实物简化为二维,艇体两侧的流体不再存在,只在艇底部流过,导致流速加快,从而加剧了滑行艇纵摇与垂荡的耦合运动的剧烈程度,船体发生了严重的振荡,艇体由于垂荡运动的惯性发生了脱离水面的现象,造成了升力的锐减。在图3c中,依据文中所设定的坐标系和右手法则,逆时针方向为正,可以看出当力矩系数绝对值在FV=1.5时突然增加,滑行艇出现了明显的抬首现象。 图3 不同Fv数下二维滑行艇阻力、升力及力矩变化特性Fig.3 The characteristics for (a)resistance, (b)lift and (c)moment of the 2D p lanning b oat under different Froude numbers 在图4中给出了滑行艇在不同速度下滑行姿态的数值模拟结果。结果表明,滑行艇在航行过程中,在给定的主机功率下滑行艇将产生初始航速,并出现初始攻角,产生的升力将使艇体抬升一定的高度,同时升力对艇体重心产生俯仰力矩,从而使滑行艇原来的平衡状态被打破。为达到新的动态平衡,艇体在不断变化的垂向力及俯仰力矩作用下产生升沉及纵摇运动,同时艇体的排水体积与湿面积同时发生变化,改变了滑行艇的直航阻力,从而使滑行艇的航行速度发生变化;而航速的改变又引起了滑行艇升力、纵摇角以及俯仰力矩的变化。当滑行艇所受的垂向合力及合力矩为零,且纵向合外力亦为零时,滑行艇的航行状态达到了动态平衡[7],滑行艇将保持这一姿态稳定航行,直到再次受到外界扰动。在本文的数值计算模型中,由于滑行艇的航行速度为定值,所以滑行艇最终只是趋近于动态平衡。 图滑行艇在不同速度下滑行姿态Fig.4 The planning style of the p lanning b oat under different velocities 在图 5 中给出了 FV=0.5、1.0、1.5、2.0 时艇体重心位置的变化曲线,反映了滑行艇的升沉变化规律。 图5 不同傅汝德数下滑行艇升沉变化特性Fig.5 The characteristics of the heave for the p lanning b oat under different Froude numbers 从总的趋势看,FV=0.5时,艇体呈现上浮状态,但在60 s之前,艇体在垂荡过程中略有下沉,只在运动趋于稳定过程中艇体逐渐上升。因为速度较低,艇体的垂荡不是很剧烈。在100 s之后艇体的垂荡幅度已很小,控制在±0.005 m左右,但是艇体的姿态依然没有趋于稳定。 当 FV=1.0 时的升沉量较 FV=0.5 时有所加剧。首先是因为速度的增大,再者是我们在前面描述过的垂荡、纵摇以及推进速度三者应该是一直处于动态变化直至垂向合力为零、纵摇合力矩为零、x方向合力为零。在本文中,由于推进速度为固定值,在此速度下,纵摇与垂荡只能是在变化中努力趋向“动平衡点”,却达不到实际航行的理想状态。 当FV=1.5时的耦合运动是滑行艇的最佳航行状态,在60 s时垂荡已基本趋于定值,80 s后已无波动,说明采用CFD软件来模拟二维滑行艇的响应运动具有一定的合理性。在此推进速度下,纵摇与垂荡达到了“动平衡点”。 当FV=2.0时的升沉幅值出现了大幅度的振荡,而且从图4c和图4d所示的滑行姿态可以看出,艇体在高速情况下已脱离水面,这也是升沉值如此振荡的原因所在。该结论与文献[6]中所模拟的三维船体运动所得结论一致,即在高速航行时传船体将产生不稳定水动力行为,出现严重振荡现象。 图 6 给出了 FV=0.5、1.0、1.5、2.0 时纵摇角变化曲线。当FV=0.5时100 s之后随着升沉幅值的趋于定值纵摇值亦基本趋向定值0.042°;当FV=1.0 时纵摇角发生振荡。不难发现,当 FV=1.0 时的纵摇角为正,而当FV=0.5时的纵摇值为负。按照坐标指向,正值时艇体为俯首,也就是说在低速时艇体会出现俯首现象,在中高速航行时会出现抬首现象,这与文献[5]中所得结论一致。此结论在FV=1.5 和 FV=2.0 时同样出现。 FV=1.5 时纵摇角随着升沉值的稳定也很快稳定在0.38°;FV=2.0时艇体发生严重振荡,纵摇值也发生大幅度振荡。 图6 不同傅汝德数下滑行艇纵摇变化特性Fig.6 The characteristics of the pitch of the p lanning b oat under different Froude numbers 艇底滑行面上的动压力是艇体产生动升力的主要原因,图7给出了120 s时刻对应的滑行艇底部动压力云图。从图中可以可出,随着速度的增大底部动压力增大,而且动压力中心位置后移。 图7 120 s时的滑行艇底部动压力云图Fig.7 The distribution of the bottom dynamic pressure under different Froude numbers at 120 s 本文针对滑行艇的实时运动响应进行了数值模拟。根据流体动力数值计算结果实时求解滑行艇的运动响应特性,在4个不同体积傅汝德数FV=0.5、1.0、1.5、2.0 下,对滑行艇的纵摇与垂荡耦合运动进行了预报及分析。其中FV=1.5时滑行艇达到稳定滑行状态的时间为80 s。此外,除FV=2.0时艇体发生严重振荡,其余情况下滑行艇均能趋于一种平衡状态。 [1] SATO Y, MIYATA H, SATO T.CFD simulation of 3-dimensionalmotion of a ship in waves:application to an advancing ship in regular heading waves[J].Journal of Marine Science and Technology,1999,4(3):108-116. [2]WEYMOUTH G D,WILSON R V,STERN F.RANSCFD predictions of pitch and heave ship motions in head seas[J].Journal of Ship Research, 2005,49(2):80-97. [3] 张怀新,刘应中,缪国平.带自由面三维船体周围粘性流场的数值模拟[J].上海交通大学学报,2001,35(10):1429-1432. ZHANG H X, LIU Y Z, MIAO G P.Numerical simulation of t h ree-dimensional viscous flow with free surface about a ship[J].Journal of Shanghai Jiaotong University,2001,35(10):1429-1432. [4] 王兆立,牛江龙,秦再白,等.基于CFD理论的滑行艇阻力数值计算[C]//第十四届中国海洋(岸)工程学术讨论会论文集.内蒙古,呼和浩特,2009:309-315. [5] CARRICA PM,WILSON R V,NOACK R W,et al.Ship motions using single-phase level set with dynamic overset grids[J].Computers and Fluids,2007,36(9):1415-1433. [6] PANAHIR,JAHANBAKHSN E,SEIFM S.Towards simulation of 3D nonlinear high-speed vesselsmotion[J].O-cean Engineering,2009,36(3/4):256-265. [7] 奚炜.翼滑艇运动智能控制仿真初步研究[D].镇江:江苏科技大学,2006. XI W.Initial study on simulation of planing hydrofoil crafts's motion and intelligent cortrols [D].Zhenjiang:Jiangsu University of Science and Technology,2006. Numerical Prediction and Analysis on the Heave and Pitch Motion of Two Dimensional Planning Boat Jin Wen-ju W ang Zhi-dong Li Li-jun Yang Shuang Th e analytical solution for analyzingmotion responses of the two dimensional planning boat in the uniform flow is presented by the CFD software.The results of the fluid dynamics are used to derive the motion responses of the planning boat.Numerical simulations of the pitch and heave coupled motion were performed under four different Froude numbers.The characteristics ofmagnitude of the heave and trim angle vary ing with the time, as well as the law of resistance, lift and moment change ing with the Froude numberswere derived.In addition, the period of the stable state when the planning boat can be reached and the dynamic pressure at the bottom of the planning boat when in sliding condition were also analyzed.Results show that the time needed for reaching the stable state need only 80 seconds under Froude number 1.5, and the planning boatwill tend to be in a “dynamic -balance” state except for the serious oscillation under Froude number 2.0. CFD; planning boat; heave; pitch U661.3 A 1673-3185(2011)06-66-05 10.3969/j.issn.1673-3185.2011.06.013 2010-10-29 晋文菊(1985-),女,硕士研究生。研究方向:船舶流体力学。E-mail:jinwenju.1314@163.com 王志东(1969-),男,博士,教授。研究方向:船舶海洋结构物的流体性能。E-mail:cywzd@sina.com3.1 不同F V数下滑行艇的水动力性能
3.2 滑行艇的升沉纵摇运动特性分析



3.3 滑行艇底的动压力分布规律
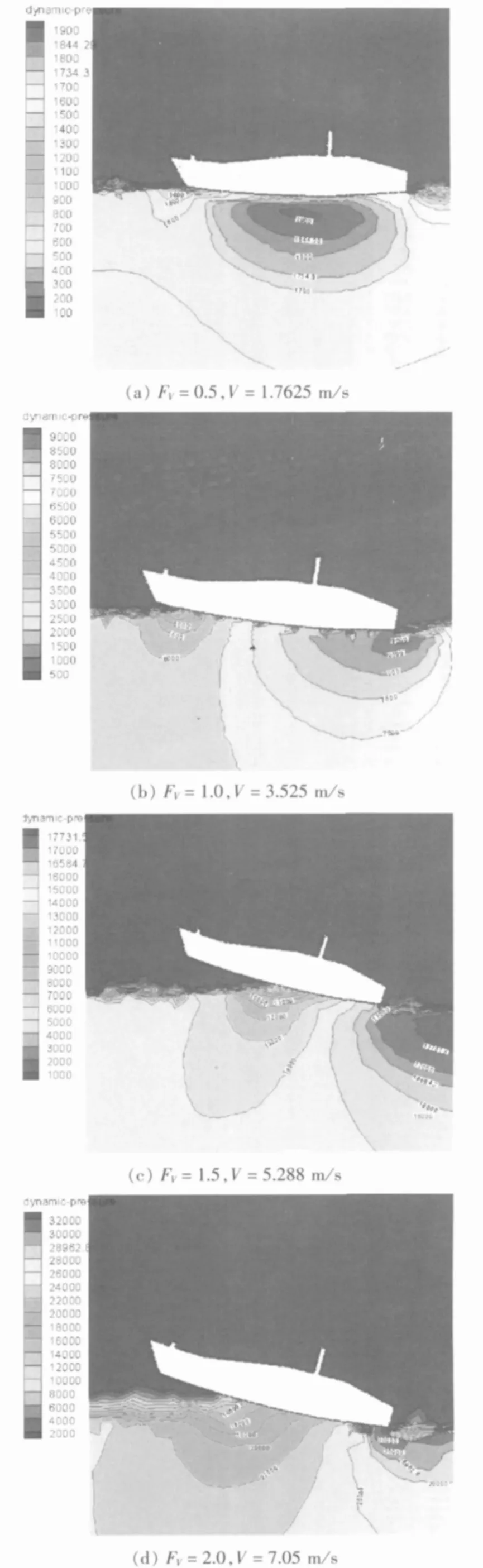
4 结论
College of Marine and Shipbuilding Engineering, Jiangsu University of Science and Technology,Zhenjiang 212003,China
