水下冲击波作用下结构损伤的数值预报误差分析

张艺凡 宗 智 张文鹏

大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部，辽宁 大连 116024

水下冲击波作用下结构损伤的数值预报误差分析

张艺凡 宗 智 张文鹏

大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部，辽宁 大连 116024

准确模拟结构在水下爆炸冲击波作用下的损伤是水下爆炸数值仿真中的难点，有必要研究数值预报误差及其产生的原因。采用ABAQUS提供的声固耦合方法，研究方板模型水下爆炸数值计算的误差。将几何模型划分为3个不同的有限元模型，分析了网格大小对计算结果的影响，以及声固耦合方法的计算误差。通过方板模型仿真、实验室水池试验和方板实船水下爆炸实验结果的比对分析表明：数值计算结果与实验值间的误差约在30%以内。总波和散波两种流固耦合计算方法的误差及其产生原因分析表明总波计算公式存在夸大空化对结构影响的可能。

水下冲击波；塑性变形；误差分析；流固耦合

1 引言

水下爆炸会产生很大的冲击载荷使附近的水中结构物产生损伤。因此，从二战以来，水下爆炸产生的结构损伤问题成为各国海军关注的焦点问题。

在过去60年间，对于结构在水下冲击波作用下的弹性响应［1］，出现了许多成熟的理论和计算方法。比如，Huang［2］提出的声学耦合理论方法，Geers［3－4］和 Deruntz［5］提出的 DAA 方法都可 以精确地预测水下爆炸所引起的结构弹性响应。通过商业软件，比如ABAQUS和LS－DYNA也可以实现结构在水下爆炸载荷作用下动态弹性响应的计算。

然而，一旦结构变形超过了弹性进入塑性，无论是理论值还是数值模拟往往与实验结果吻合得不好。早在二战时期，Kirkwood［6］就研究过圆板受水下冲击波载荷的塑形变形，提出了结构的损伤机理，但是计算得到的结果远远小于实验值。Zong［7－8］基于 Kirkwood 的理论，对损伤机理进行了改进，大大提高了理论预测的精度。吴成［9］研究了方形板的损伤。朱锡等［10］研究了板架在水下爆炸作用下结构损伤。但是，系统地用数值方法预报结构在水下冲击波作用下产生的损伤的研究还不够。特别是对于任意给定的一个结构，使用数值方法对其损伤（或者塑性变形）进行预报时，往往很难得到令人满意的结果。

其原因在于其中涉及的流固耦合作用尚不明确。本文使用声固耦合方法，通过对两个实验结果和一个实船试验结果的对比分析，考察数值模拟预报水下爆炸造成的损伤方面存在的误差，希望对数值方法的使用提供有益的参考。

2 计算方法简介

本文在进行数值仿真计算时，计算方法采用ABAQUS提供的声固耦合方法。关于这方面的介绍在许多论文中均有涉及，对此不再赘述。需要强调的是ABAQUS中提供的两种载荷计算方法：不考虑空化的散波公式法和可以考虑空化的总波公式法。在线性假设下，水中冲击波可以分为三个部分：不考虑结构存在时，由爆源传播到空间某一点的压力，称为冲击波；假设结构是刚体，入射冲击波打到结构上产生的反射波；辐射波是指在没有入射波和反射波时，结构在水中振动产生的波。在这种假设下来建立求解方法的就是散波公式法，如图1所示。

图1 水中冲击波示意图Fig.1 Schematic of underwater shock

当结构的变形速度较大时，结构前的压力就会降到蒸气压力以下，从而发生空化现象。

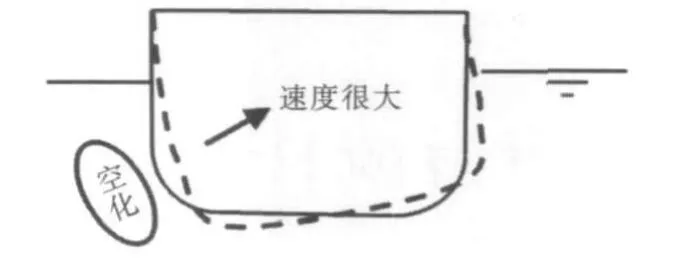
图2 水中空化示意图Fig.2 Schematic ofwater cavitation

考虑到这种空化现象的计算方法就是总波公式法。空化现象改变了附近流场的压力分布，从而使得水域的加载方式有所不同。

通过这两种方法计算得到载荷，就可以通过耦合的方法来计算结构的损伤。流固耦合计算方法在流体区域求压力时，满足速度边界条件；而在求解结构位移时，冲击波压力作为力的边界条件加入到结构的控制方程中。

水中冲击波入射波的计算在远场往往采用如下经验公式：

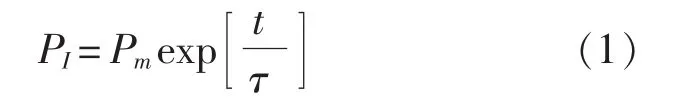
对于TNT炸药峰值Pm和衰减常数τ采用如下公式获得：

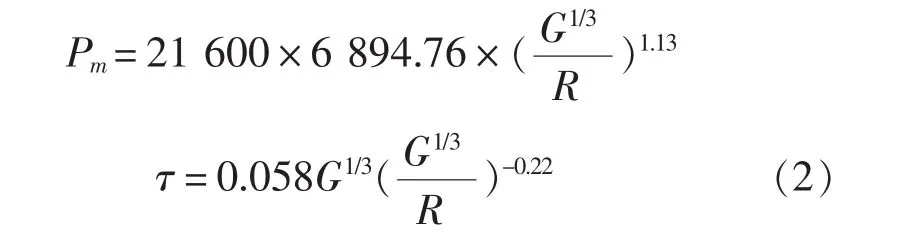
式中，G为炸药质量，kg；R为爆炸距离，m。该公式直接由实验值获得，具有很高的精度。同时，结构在空气中的损伤计算也很成熟，具有较高的精度。因此，水中冲击波造成结构损伤的数值模拟计算误差最有可能来自于载荷计算方法和流固耦合方法中的误差。

本文将通过3个具体的例子来考虑数值模拟的误差问题。

3 数值模拟的收敛性分析

数值模拟计算必须进行收敛性验证。收敛性是指数值模型计算网格越细，数值结果越接近真实值。一个数值方法只有具有收敛性才可以使用。

为考察收敛性，我们取一块方板模型进行水下爆炸数值计算，结构参数和计算工况如表1所示。

表1 计算模型尺寸参数Tab.1 Parameters of calculation model

对于数值计算问题，建立的有限元模型会对最终的结果产生较大影响。本文计算模型中，主要影响参数为流场大小和有限元网格尺寸。流场大小的影响分以下3个方面：重力影响、阻尼影响和惯性影响。通常比较关心的是惯性影响，此时部分流场将参与船体的总振动，该部分流场质量称之为附连水质量，与结构本身质量为同一量级，在计算时附连水质量不可忽视。

在进行水下爆炸数值模拟分析时，为获得较准确的模拟数据，必须保证流场区域足够大。但是，由于现有计算软件对数值模型单元数的限制，流场区域不可能取为无限大。表2［11］给出了随着流场尺寸与结构尺寸比值的变化，相应附加质量率的变化值。本文中，流场尺寸表示流场边缘到板中心的长度，结构尺寸表示板边缘至板中心的长度，附加质量率表示无限流场的附加水质量与有限元模型流场的附加水质量的比值。

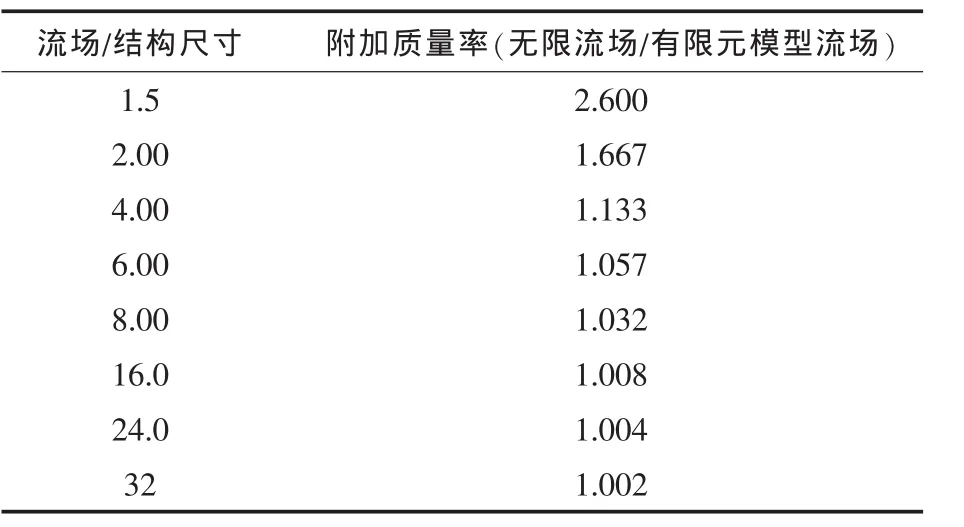
表2 有限元模型中流场大小与附加质量率的关系Tab.2 The relationship of add ed mass ratio and finite element size of flow field

为提高精度并合理安排计算周期，本文中流场尺寸与结构尺寸之比取6。几何模型如图3所示，其中，z方向为垂直于板面的方向，x方向为沿板长度方向。

图3 几何模型示意图Fig.3 Geometrymodel

为分析网格大小对计算结果的影响，对上述几何模型划分为3个不同的有限元模型进行计算。模型中板结构采用壳单元，流场单元采用六面体声学单元，流场大小为4.2m×2.4 m×2m，表3中给出了流场单元的尺寸，流场网格大小如图4所示。板单元的大小与相对应的流场单元大小相同。

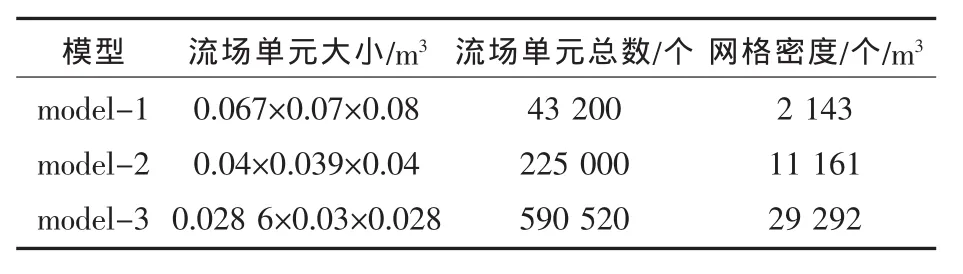
表3 有限元模型流场单元尺寸Tab.3 Size of finite elements of flow field

图4 不同尺寸流场网格示意图Fig.4 Different sizes of finite element flow field

数值计算时采用总波公式（在ABAQUS中通过关键字Totalwave实现）进行显式动态分析计算。板材料为钢，在计算中材料考虑率相关的影响，采用目前普遍接受的Cowper－Symonds提出的本构方程形式：

水域与结构接触面设置声固耦合条件，以传递压力和位移。关键字设置为：

其中，Water－Surface为与结构接触的水域，Structure－Surface为与水域接触的结构面。

为消除水域边界的影响在模型边界上定义无反射条件，表示冲击波可以穿过该表面而不发生反射。本文计算模型的水域边界形状均为平面，分别对模型边界面采用如下关键字进行设置：

*SIMPEDANCE，NONREFLECTING＝PLANAR

Water－1

其中Water－1表示水域模型边界面。通过如上所述的设置后，提交任务进行计算，施加的冲击波载荷如图5所示。

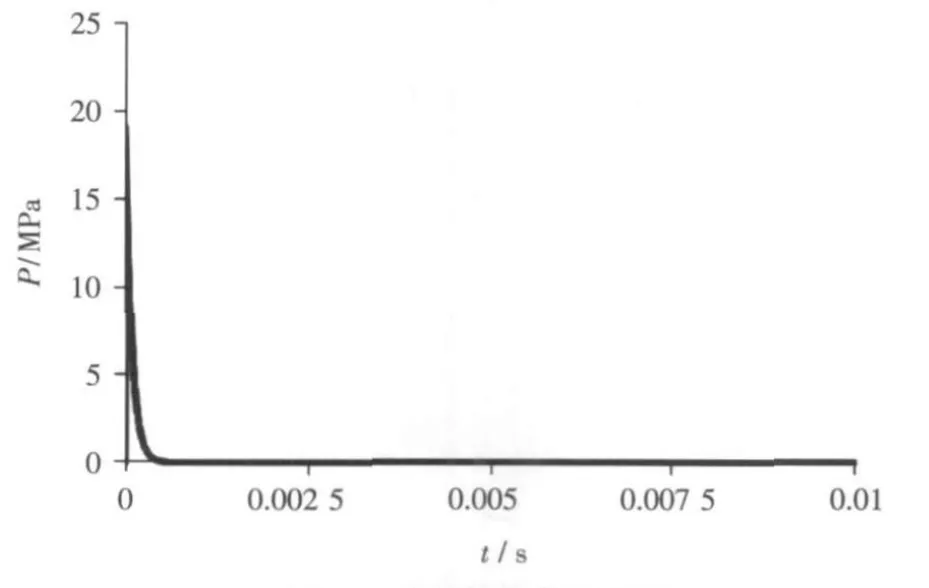
图5 冲击波载荷示意图Fig.5 The curve of shock pressure

计算得到3个模型中心点的挠度，如图6所示。

图6板中心点挠度示意图Fig.6 The displacement of the center of plate

通过对计算结果的分析可以看出，模型model－1 与 model－2 之间的误差为 1.65%，model－2 与model－3之间的误差在 1.24%。因此，在本算例中，当流场网格密度达到11 161个／m3时，数值计算即可认为收敛。计算时，为排除计算时间步长对结果的影响，采用ABAQUS提供的自动匹配时间步长设置以保证计算精度。

4 实验室试验的对比研究

首先考虑两块圆板的损伤，通过对具体实验工况的数值模拟，将计算得到的结果与Kirkwood的实验结果进行比较。这两项实验在水池中进行，炸药当量很小。板的尺寸和爆炸工况如表4所示。

表4 计算模型尺寸参数Tab.4 Parameters of calculation model（Steel 1）

对于第一块板进行计算时共划分了105个六面体流场单元和300个壳结构单元。水中声速取为1 500m／s。分别采用散波公式和总波公式计算Steel1的损伤情况。数值计算模型如图7所示。

图7 有限元模型Fig.7 Finite elementmodel

载荷的计算采用ABAQUS提供的水下爆炸载荷计算公式进行加载。载荷参数具体设置如下：

将数值计算得到损伤结果与实验值进行对比，如图8所示。

图8 Steel1中心点位移示意图Fig.8 The displacement of the center of Steel 1

图为Steel 1中心点的塑性位移情况。

从图8中可以看出，散波计算的误差比较小，为16.8%；总波计算的误差为28.9%，比散波高一倍左右。在ABAQUS提供的两种声固耦合计算方法中，散波公式将水压力简化为线性问题；而对于空化这类非线性问题只能采用总波公式［12］。因此，通常分析认为总波计算能够考虑空化现象，理应更加准确，但在本例中总波公式计算产生的误差更大，分析其原因，很可能在于不恰当的考虑了空化效应。

为说明这一点，观察Steel 1附近流场区域空化现象的演化过程。如图9所示，从图中可以清楚的看到冲击波的传播路径。

为更清楚的观察到空化区域的扩展，对流场压力的显示数值进行调整，仅取板周围的流场压力云图进行分析，如图10所示。当计算至0.08 ms时，与板直接接触的部分流场出现空化现象，随着计算时间的推移空化区域迅速扩大。

图9 Steel 1流场压力云图Fig.9 Plot ofwater pressure of Steel 1

图10 Steel 1空化区域云图Fig.10 Plotof cavitations of Steel 1

图中浅灰色的区域为空化区域。通过简单的计算可以得到，流场内空化区域的传播速度约为1 500 m／s，远远大于实际中空化的传播速度（约10～20m／s），空化效应对结构的影响被放大。

另外，我们还计算了另外一块圆形板Steel 2在水下冲击波作用下的响应情况，几何参数和计算工况见表5，图11分别给出了总波和散波计算所得到的塑性变形时程曲线。

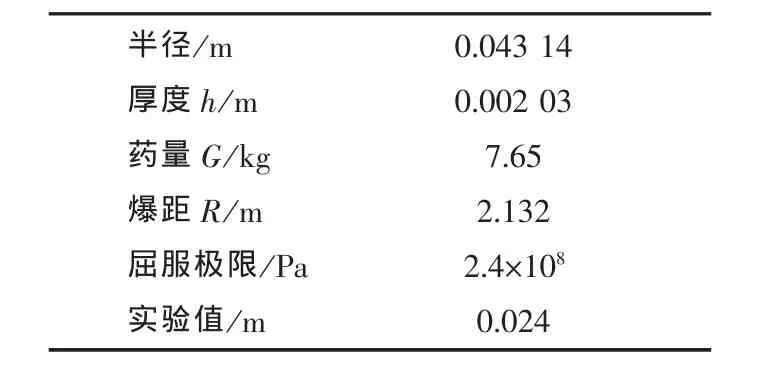
表5 计算模型尺寸参数Tab.5 Parameters of calculation model（Steel 2）

同样的散波计算的误差为6.33%，比总波计算的误差13.8%小的多，其原因是由于总波计算法过分地夸大了空化的作用。

比较图8和图11可以看出，Steel 2的计算结果误差比较小。产生的原因可能为Steel 2的相对变形（变形量 ／板的直径）近似为 0.55，而 Steel 1的相对变形量为0.11。由于Steel 2的相对变形大，塑性变形成为整个变形过程中的主要因素，比较容易捕捉；Steel 1的相对变形较小，弹性变形的影响变得不可忽视。

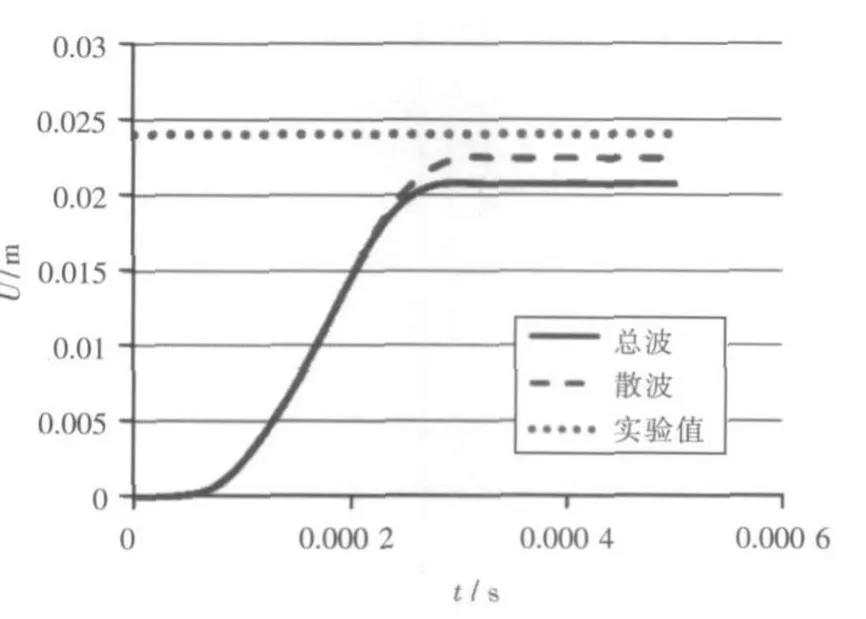
图11 Steel 2中心点位移示意图Fig.11 The displacement of the cent er of Steel 2

5 实船试验对比研究

另外，对一块实船上的方板以及该实船的水下爆炸作用下的试验结果与数值计算进行了比较。板的几何尺寸和爆况如表6所示。

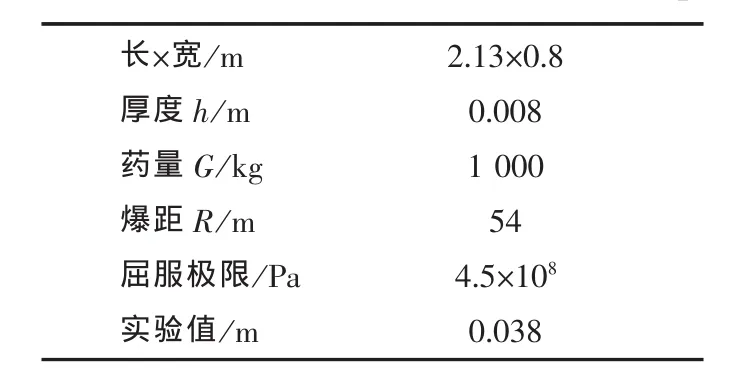
表6 计算模型尺寸参数Tab.6 Parameters of calculation model（Ship 1）

计算共划分了260个板单元，流场大小为4.8m×12.78m×6m， 流场单元总数为 556 800。图12所示为总波计算和散波计算的损伤模拟结果。

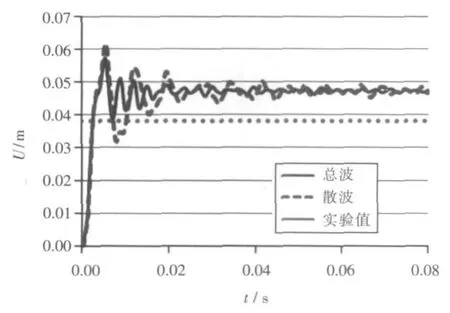
图12 Ship 1中心点位移示意图Fig.12 The displacement of the cent er of Ship 1

Ship 1总波计算和散波计算结果与实验值的误差分别为25.05%和22.73%。两者数值相近。说明在实际应用中，总波和散波公式的精度区别不大。而在实验室条件下，总波的公式结果都比散波大（Steel 1和Steel 2），说明总波计算公式有夸大空化的可能，但这一结论还需更多的研究来验证。

6 参数分析

为比较各个计算参数变化对结果的影响，对屈服极限、药量和爆炸距离分别进行了参数分析。对Ship1模型分别计算表6所给出的6种工况下的塑性位移情况。

计算得到板的塑性位移的变化量如表7所示。

表7 计算工况Tab.7 Calculation condition s

表8 位移变化率计算结果Tab.8 Calculation results of various displacement ratio

通过表格中的数据分析我们可以看出，当计算参数值各变化10%时，对计算结果均会产生一定的影响，其中爆炸距离变化对计算结果产生的影响最大。在实船实验中，材料、爆炸距离等参数都会产生一定的测量误差，使得数值计算的结果与实验值的误差增大。

7 结 论

1）对于实验室试验，由于可控性好，散波公式法精度明显高于总波公式计算法，说明总波公式可能夸大了空化效应的影响。

2）根据实船试验结果对比分析，总波公式和散波公式计算误差相差不大。

3）水下爆炸损伤的数值预报是一个非常复杂的问题，在现有的计算水平下计算误差达到30%还是令人满意的。从这个意义上讲，本文所讨论的声固耦合计算方法可以应用于实际工程预报中。同时，为了进一步提高精度，还需要做更多的计算方法研究工作。

［1］ JONESN.Structural impact［M］.Cambridge： Cambridge University Press，1989：333－383.

［2］ HUANG H，Wang Y F.Transient interaction of spherical acoustic waves with a cylindrical elastic shell ［J］.Journal of the Acoustical Society of America， 1970，48：228－235.

［3］ GEERS T L.Residual potential and approximatemethods for three－dimensional fluid－structural interaction problem［J］.Journal of Acoustic Society of America，1971，49（5B）：1505－1510.

［4］ GEERS T L.Doubly Asymptotically approximations for transient analysis of submerged structures ［J］.Journal of Acoustic Society of America，1978，64（5）：1500－1508.

［5］ DERUNTZ J A.The underwater shock analysis code and its applications［C］//Proceedings of 60th Shock and Vibration Symposium，Virgina，USA，1989.

［6］ KIRKWOOD JG，RICHARDSON JM.The plastic deformation of circular diaphragms under dynamic loading by an underwater explosion wave［R］.OSRD 4200，1944.

［7］ ZONG Z，LAM K Y， LIU G R.Probabilistic risk p rediction of submarine pipelines subjected to underwater shock［J］.Journal of Offshore Mechanics and Arctic Engineering，1999，121（4）：251－254.

［8］ ZONG Z，LAM K Y.Viscoplastic response of a circular plate to an underwater explosion shock［J］.Acta Mechanica，2001，148（1/4）：93－104.

［9］ 吴成，金俨，李华新.固支方板对水中爆炸作用的动态响应研究［J］.高压物理学报，2003，17（4）：275－282.

WU C，JIN Y，LIH X.A study on square plate dynamic response under underwater explosion ［J］.Chinese Journal of High Pressure Physics，2003，17（4）：275－282.

［10］ 朱锡，白雪飞，黄若波，等.船体板架在水下接触爆炸作用下的破口试验［J］.中国造船，2003，44（1）：46－52.

ZHU X，BAI X F，HUANG R B，et al.Crevasse experiment research of platemembrance in vessels subjected to underwater contact explosion ［J］.Shipbuilding of China，2003，44（1）：46－52.

［11］ ABAQUSusermanual ver.6.9EF［S］.ABAQUS， Inc..

［12］ ABAQUS analysis user’smanual，23.3.1 ［S］.ABAQUS，Inc.

Error Analysis of Numerical Prediction of Structure Damages Subjected to Underwater Shock

Zhang Yi－fan Zong Zhi ZhangWen－peng
Faculty of Vehicle Engineering and Mechanics，State Key Laboratory of Structural Analysis for Industrial Equipment， Dalian University of Technology，Dalian 116024，China

The fas t development of computing technology saw wide applications of numerical simulations in underwater explosion in recent years，but it′s still difficult to numerically and exactly predict the damages of amarine structure subjected to underwater shock.It is true that the numerical results and experimental results of a certain underwater explosion problems are in good agreement，but in themost general cases， the problem that how good the numerical results agree with experimental results remain unsolved.In this paper， through three examples， we try to reveal the numerical errors compared with experimental results.All of the three examples show that the numerical errors can be controlled within 30 percent.Two numerical methods， that is， total wave and scatter wave formulations， are employed in this paper.It seems that the totalwavemethod overestimates the effect of cavitations.

underwater shock； plastic deformation； error analysis； fluid structure interaction

U661.41

A

1673－3185（2011）06－38－07

10.3969/j.issn.1673-3185.2011.06.008

2010-08-02

国家自然科学基金（50921001）；973项目（2010CB832700）

张艺凡（1986－），女，硕士研究生。研究方向：流固耦合，水下爆炸。E-mail：yifanzhang929＠gmail.com

宗 智（1964－ ），男，教授，博士生导师。 研究方向：水下爆炸，流固耦合。E-mail：zongzhi＠dlut.edu.cn