Sylvester不等式猜想研究

岳育英，刘兴祥，白春红

（延安大学 数学与计算机科学学院，陕西 延安 716000）

Sylvester不等式猜想研究

岳育英，刘兴祥，白春红

（延安大学 数学与计算机科学学院，陕西 延安 716000）

从 Sylvester不等式出发，并将其推广到 n个矩阵的情形，其次利用广义初等变换及互素多项式的有关性质及推论给出使 Sylvester不等式猜想成立的充分条件，最后在此充分条件下将所讨论的矩阵推广到更一般的形式并给出了一系列与其相关的重要结果。

Sylvester不等式；互素多项式；广义初等变换；秩；矩阵

0 预备知识

引理 1［1］（Sylvester不等式）设 A∈Fm×n，B∈Fn×s，则 rank（AB）≥rank（A）＋rank（B）－n.

引理 2［2］（Frobenius不等式）设 A∈Fm×n，B∈Fn×s，C∈Fs×t，则

rank（ABC）≥rank（AB）＋rank（BC）－rank（B）.

在引理2中，只须令 B＝En，就得到引理1。

这两个不等式最初分别是由 Sylvester和 Frobenius首先证明的［3，4］。目前这两个不等式已成为众多矩阵理论教科书中的经典结论，多是用广义初等变换证明的。

引理 3［5］设 fi（x），gj（x）∈F［x］（i＝1，2，...，n，j＝1，2，...，m），则

引理 4［6］∀m，n∈N＋，设 f（x），g（x）∈F［x］，若 (f（x），g（x ）)＝1，则（fm（x），gn（x））＝1。

引理 5［6］设A∈Fm×n，B∈Fs×t，则 rank( )A ＋

推论 1 设 A∈Fm×m，B∈Fn×n，则 rank( )A ＋

推论 2 设A∈Fm×m，B∈Fm×m，则 rank()A ＋

我们将用上面几个引理找出Sylvester不等式猜想成立的条件。Sylvester不等式的猜想如下：

猜想 1 设A∈Fn×n，k1，k2，…，kt∈F，当k1，k2，…，kt满足什么条件时，有

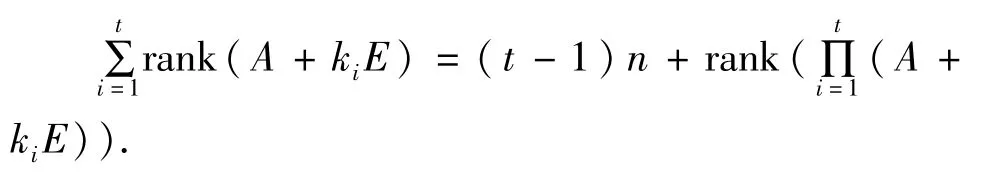
1 主要结果

引理1和引理2可推广到n个矩阵，于是就有如下两个定理：

定理1 （推广的 Sylvester不等式）

设 n，k1，k2，...，kn∈N＋，Ai∈Fki×ki＋1（i＝1，

2，...，n），则证明 （1）当n＝1，2时，不等式成立。（2）假设t（t≥3）时，不等式成立，即

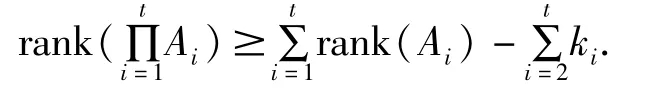
那么当 n＝t＋1时，令，由引理1就有rank（BAt＋1）≥rank（B）＋rank（At＋1）－kt＋1.

有

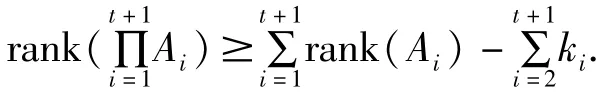
即对任意的正整数 n，结论成立。

推论 3 设n∈N＋，A∈Fn×n，则 rank（Ak）≥k（rank（A））－n（k－1）.

定理 2 设 n，k1，k2，...，kn，kn＋1∈N＋，Ai∈Fki×ki＋1（i＝1，2，...，n），则n≥3时有

推论 4 设 n∈N＋，A∈Fn×n，则rank（Ak）≥（k－1）rank（A2）－（k－2）rank（A）.

定理3 设f（x），g（x）∈F［x］，若（f（x），g（x））＝1，A∈Fn×n，则

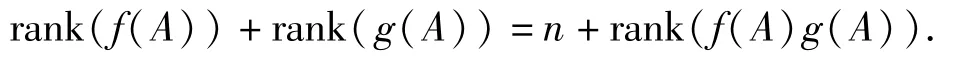
证明 由于（f（x），g（x））＝1，则存在u（x），v（x）∈F［x］，使得f（x）u（x）＋g（x）v（x）＝1，将矩阵A代入就有 f（A）u（A）＋g（A）v（A）＝E，

由推论2知

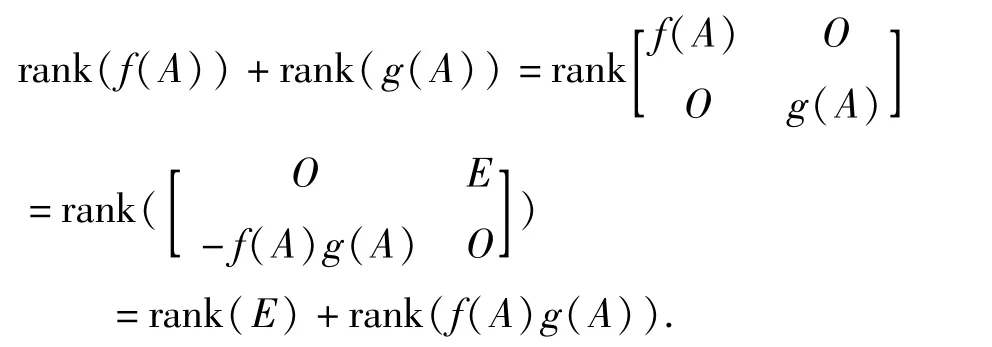
一般地，定理3可推广到 n个互素多项式的情形。

定理4 设A∈Fn×n，fi（x）∈F［x］（i＝1，2，…，m），如果fi（x）（i＝1，2，…，m）两两互素，则

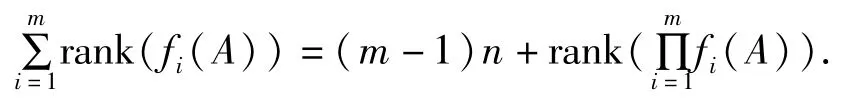
证明 （1）当 n＝1，2时上式成立；

而由定理 3知 rank（g（A））＋rank（fk＋1（A））＝n＋rank（g（A）fk＋1（A））.

由归纳法原理知定理4成立。

现结合以上引理、推论及定理给出猜想1成立的条件。

定理5 设 A∈Fn×n，k1，k2，...，kt∈F，且两两互异，则

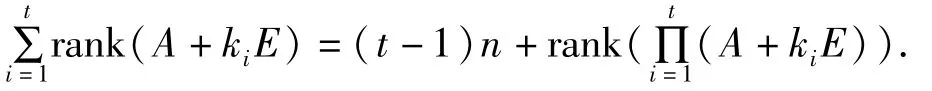
证明 设 fi（x）＝x＋ki∈F［x］（i＝1，2，...，t），由于k1，k2，...，kt两两互异，

则f1（x），f2（x），...，ft（x）两两互素，由定理3及定理4直接可得

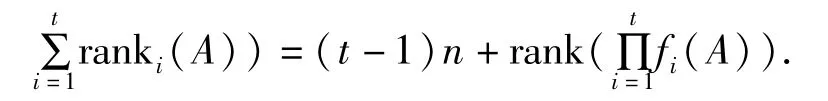
即

推论 5 设A∈Fn×n，k1，k2，...，kn是矩阵 A的n个互异的特征根，

则

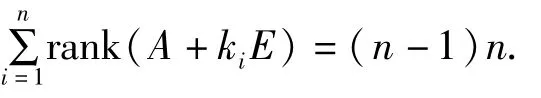
证明 由 Cayley－Hamilton定理［2］可得

推 论 6 设 k1，k2，...，kt不全 相 等，ki1， ki2，...，kim两两互异（m≤t），，则

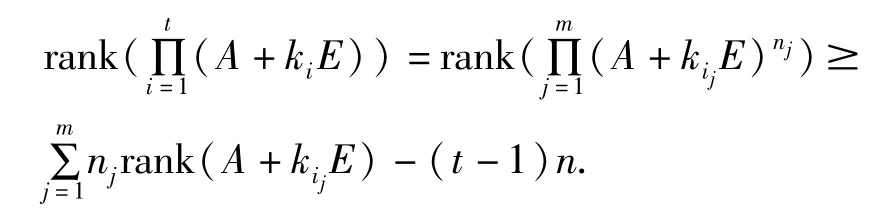
证明 记 fj（x）＝（x＋kij），fj（x）∈F［x］（j＝1，2，...，m），由于kij（j＝1，2，...，m）互不相等，那么

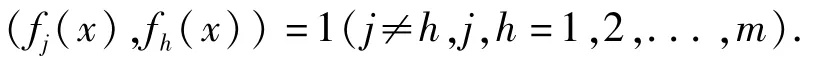
由引理4有

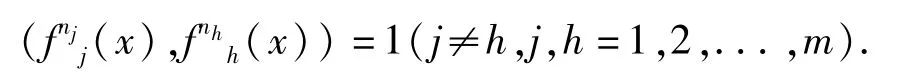
而由定理4有

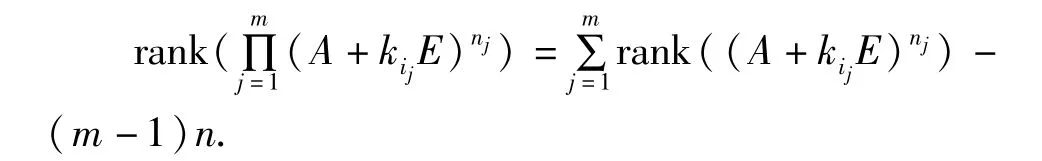
再由定理2和推论4有

所以

推论 7 若矩阵 A是幂零、幂等、对合矩阵，那么就有

其中f1（k1，k2，...，kt）和 f2（k1，k2，...，kt）是关于k1，k2，...，kt的函数，其中k1，k2，...，kt互不相等。

至此我们已经找到了猜想 1成立的条件，并给出证明，较文献［1］的方法要简单得多。

2 推广

定理 6 设 A∈Fn×n，B∈Fn×nn，AB＝BA，则对任意两两互异的数 k1，k2，...，kt∈F，有

证明 由于 B∈Fn×nn，因而可将A＋kiB转化成C＋kiE的形式。因 A＋kiB＝（AB－1＋kiE）B，且AB＝BA，所以，进而有

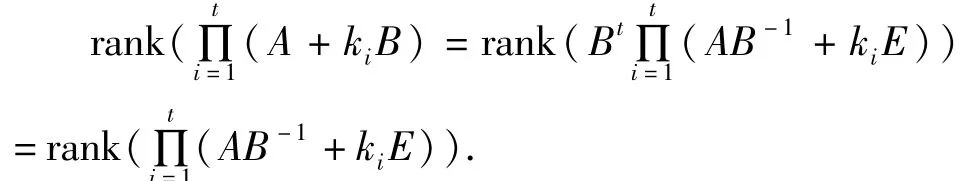
又因 k1，k2，...，kt互异，由定理4可得

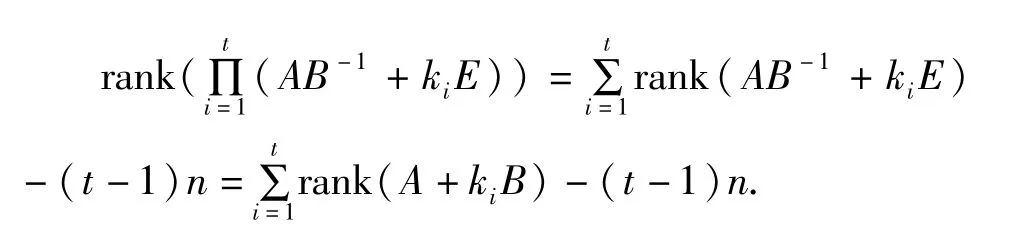
进一步还可将定理3推广至分块矩阵的情形。

定理 7 设A∈Fn×n，B∈Fn×nn，AB＝BA，kij（i＝1，...，t，j＝1，...，m）两两互异，则有

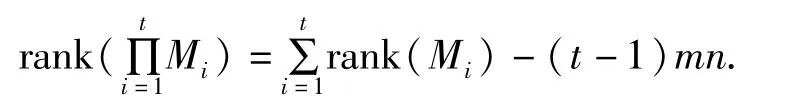
其中Mi＝diag（A＋ki1B，....，A＋kimB），i＝1，2，...，t.

（A＋kimB））且AB＝BA，进而

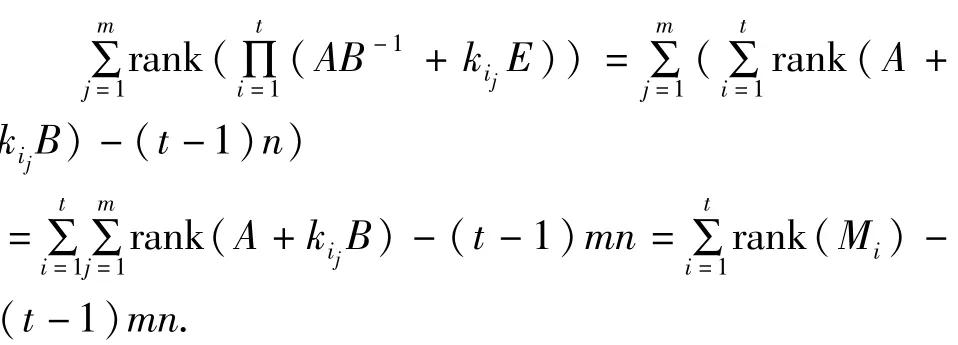
A＋kiB还有更一般的形式即推论8。

推论 8 设A，B1，B2∈Fn×n，B1－B2∈Fn×nn，则

rank（（A＋B1）（A＋B2））＝rank（A＋B1）＋rank（A＋B2）－n.

证明 由引理 5知 rank（A＋B1）＋rank（A＋

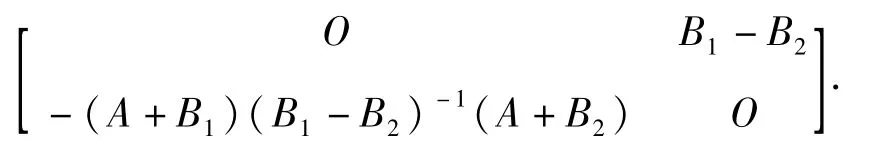
所以

［1］李书超.一类矩阵秩的恒等式及其推广［J］.武汉科技大学学报，2004，27（1）：96－98.

［2］李尚志.线性代数［M］.北京：高等教育出版社，2006：223－224.

［3］Mirsky L.An Introduction to linear algebra［M］.Oxford：Oxford University Pressk，1955：136.

［4］MarsagliacS.Equalities and inequalities for ranks ofmatrices［J］.Linear and Multilinear Algebra，1972，16（4）：269－292.

［5］北京大学数学系几何与代数研究室代数小组.高等代数［M］.3版，北京：高等教育出版社，2003：85－95.

［6］张禾瑞，郝鈵新.高等代数［M］.4版，北京：高等教育出版社，1999：186－210.

［7］王松桂，贾忠贞.矩阵不等式［M］.2版，北京：科学出版社，2006：43－46.

［8］RogerH，Charles J.Topics inmatrix analysis［M］.Cambridge：Cambridge University Press，1991：45－60.

［责任编辑 贺小林］

O151.2

A

1004-602X（2011）02-0015-03

2011 -03 -30

岳育英（1985—），女，陕西大荔人，延安大学在读硕士研究生。