两个包含近似伪 Smarandache函数的渐近公式

高 丽，谢 瑞，赵 琴

（延安大学 数学与计算机科学学院，陕西 延安 716000）

两个包含近似伪 Smarandache函数的渐近公式

高 丽，谢 瑞，赵 琴

（延安大学 数学与计算机科学学院，陕西 延安 716000）

利用初等方法研究了近似伪 Smarandache函数分别与两个特殊数论函数的复合函数在简单数序列中的均值性质，并给出了两个有规律的渐近公式。

近似伪 Smarandache函数；简单数；复合函数；渐近公式

0 引言及结论

在文献［1］中，Vyawahare定义了一个新的函数K(n)，即：对任意的正整数n，K(n)＝m，这里i＋k是使n能整除m的最小正整数。称这个函数K (n)为近似伪 Smarandache函数。在文献［2］第23个问题中，如果一个正整数n的真因子的乘积不超过n，就称n为简单数。令A表示所有简单数的集合，即有A＝｛2，3，4，5，6，7，8，9，10，11，13，14，15，17，19，21，…｝。容易看出，n有4种情形，即n＝p，或 n＝p2，或 n＝p3，或 n＝pq，这里 p，q是不同的素数（证明参见文献［3］）。令 pd(n)表示n的全部正因子的乘积，即表示n的全部真因子的乘积，即本文利用初等数论方法研究了K(pd(n))和K(qd(n))的均值性质，并给出了两个有规律的渐近公式，即证明了下面的定理（下文中出现的n，如无特殊说明，均为奇数）。

定理1 对任意的实数 x＞1，有渐近公式

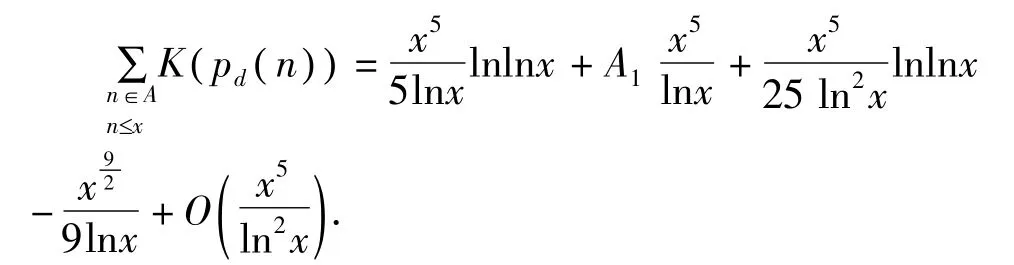
其中 A1为可计算的常数。

1 引理及证明

为了得到上述定理的证明，需要下面的两个引理：

引理1 设n为任意正整数，则有

证明 参见文献［1］。

引理2［4］设k≥0及 x≥3是实数，p，q是两个素数，B是一可计算的常数，有渐近公式

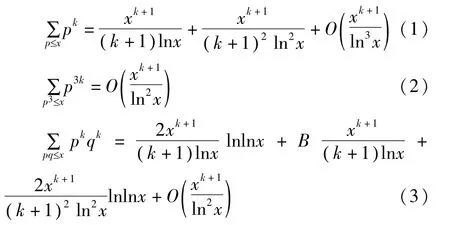
证明 应用 Abel恒等式[]5，并注意到 π()x ＝得到

应用同样的方法我们还可以得到

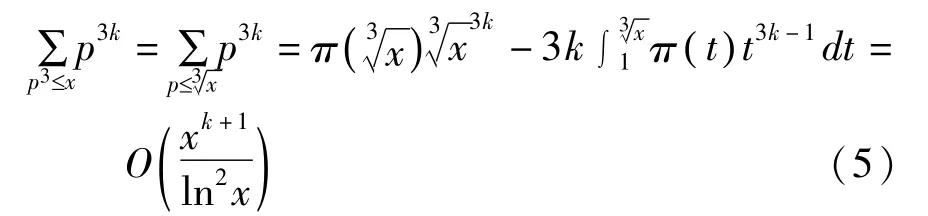
应用（5）式以及熟知的分拆恒等式可得

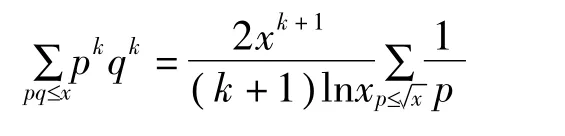
当m≥2时，有

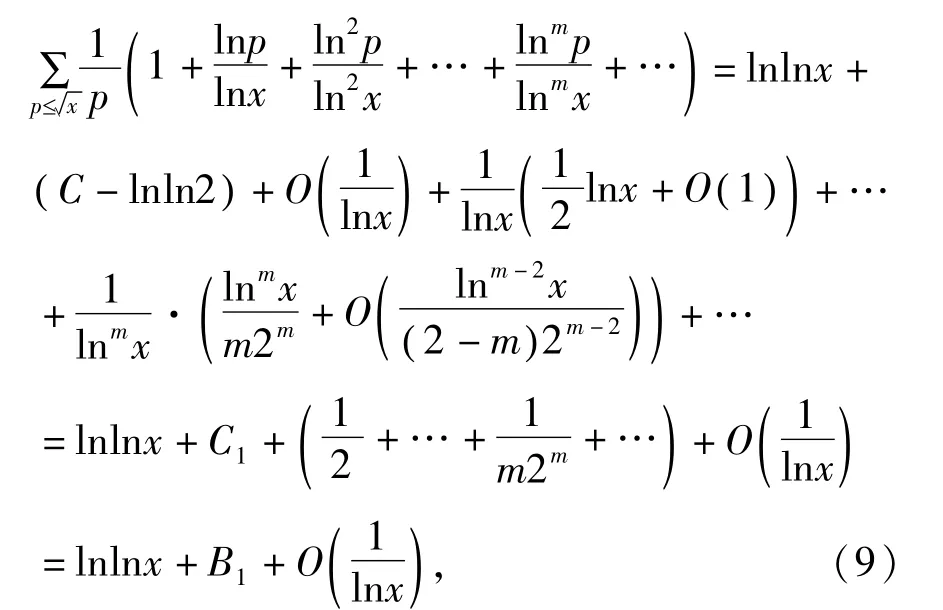
应用同样的方法可得

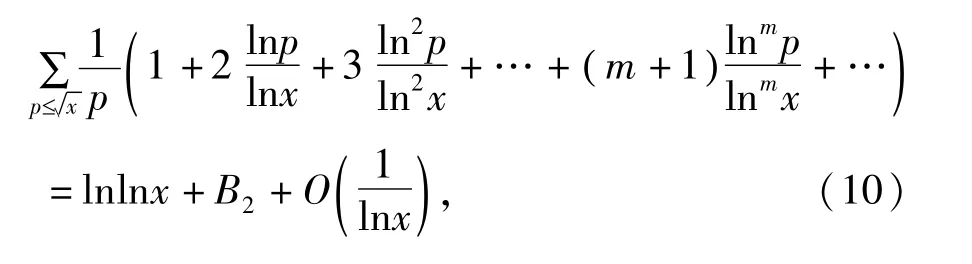
从（7）（9）（10）式容易得到

于是完成了引理2的证明。

2 定理的证明

本节来完成2个定理的证明。由引理1，引理2中（1）（2）（3）式，n∈A时n的四种情形及 pd()n的定义知

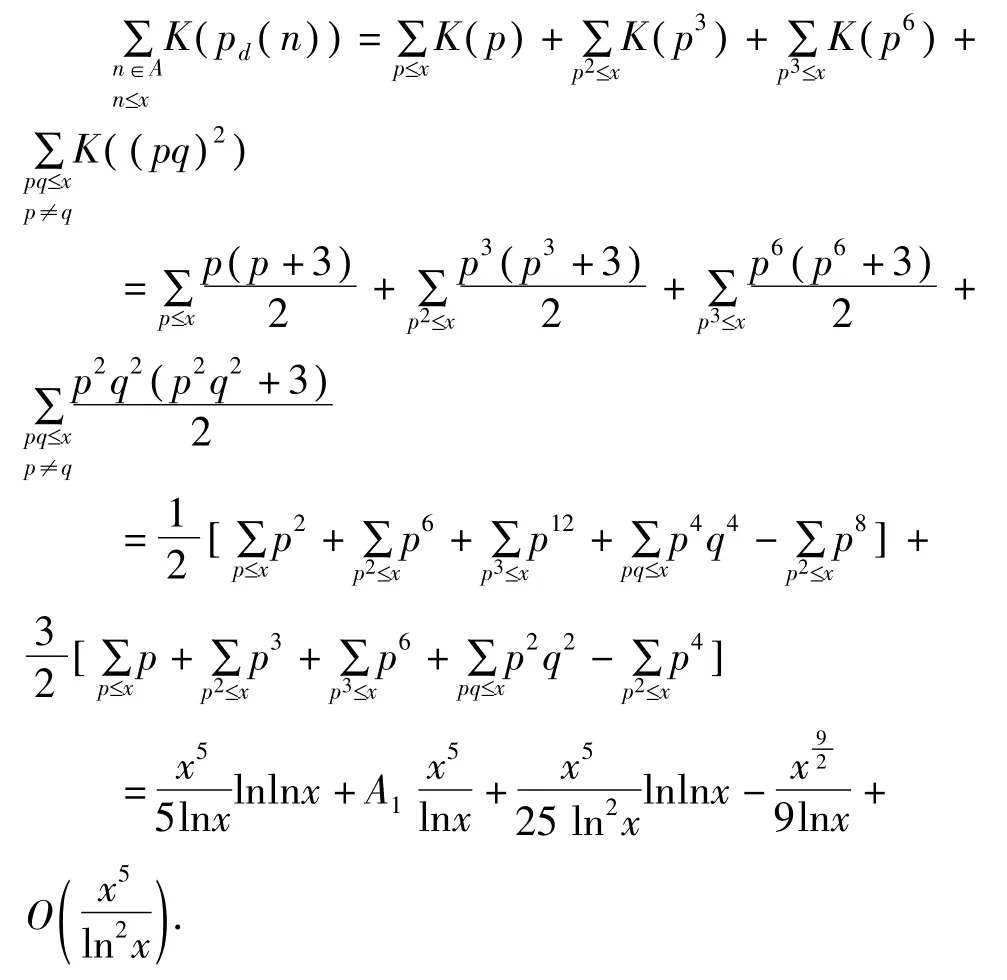
这就完成了定理1的证明。用同样的办法可以证明定理 2。由qd()n的值我们有

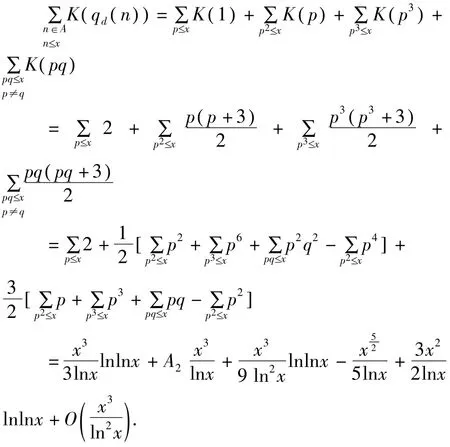
这就完成了定理2的证明。

［1］Vyawahare A W.Near pseudo Smarandache function［J］Smarandache Notions Journal，2004（14）：42－61.

［2］Smarandache F.Only problems，not solutions［M］.Chicaga：Xiquan Publishing House，1993.

［3］刘红艳.关于简单数序列的均值性质［J］.宁夏大学学报（自然科学版），2004，24（1）：28－30.

［4］朱敏慧.一个新的算术函数和它的渐近公式［J］.纺织高校基础科学学报，2007，20（4）：357－360.

［5］Apostol T M.Introduction to analytic number theory［M］. New York：Spinger－Verlag，1976.

［责任编辑 贺小林］

Two Arithmetical Functions Involving Near Pseudo Smarandache Notions and Their Asymptotic Formulas

GAO LI，XIE RUI，ZHAO QIN
（College of Mathematics and Computer Science，Yan an University，Yan an 716000，China）

By using elementarymethod，the article will study themean value properties of function of functions involving near pseudo smarandache notions and two special arithmetical functions on simple numbers respectively，a series of regular results are obtained.

near pseudo Smarandache notions；simple numbers；function of functions；asymptotic formula

O156.4

A

1004-602X（2011）02-0001-03

2011 -04 -15

国家自然科学基金资助项目（10291093）；陕西省教育厅专项科研计划项目（07JK430）

高丽（1966—），女，陕西绥德人，延安大学教授，硕士。