基于调频连续波的双基逆合成孔径雷达研究

朱小鹏 张 群 罗 迎 李宏伟

（空军工程大学电讯工程学院，陕西 西安 710077）

1.引 言

由于调频连续波（FMCW）雷达在体积小、重量轻和低截获概率等性能方面的优势［1－3］，已广泛受到雷达研究人员的关注。近年来，由于实用轻型和小型化合成孔径雷达（SAR）成像系统的需求，将FMCW雷达与SAR系统相结合逐渐成为国内外学者研究的热点问题［4－9］，主要包括引用FMCW 信号的SAR信号处理和斜视成像方面［10－12］；而将 FMCW应用到ISAR系统中具有同样的意义，针对该问题，目前国内外仅有少数几篇文献进行过报道［13］，所以对该问题的研究有待进一步的深入。同时，针对应用FMCW雷达中存在收发天线隔离度的问题，由于双基地雷达其收发分置的结构特性，在避免收发雷达干扰方面具有其天然的优势，因此，对双基地FMCW雷达的逆合成孔径雷达（ISAR）成像研究具有十分重要的实际意义和应用价值。

与传统脉冲式ISAR成像系统不同，FMCW的脉冲持续时间较长，不能采用传统的“走－停”模式。在双基地FMCW－ISAR成像系统中，目标脉内运动产生的距离快时间一次项、二次项与慢时间耦合会使目标一维距离像发生走动和主瓣展宽现象，导致目标像的严重散焦。本文通过对回波信号相位的分析得出该耦合项，分析其在距离多普勒域的表现形式及影响并给出相应的补偿算法，同时给出整个成像算法流程，并通过对点目标的仿真验证了文中分析和补偿算法的正确性和有效性。

2.双基地FMCW－ISAR模型

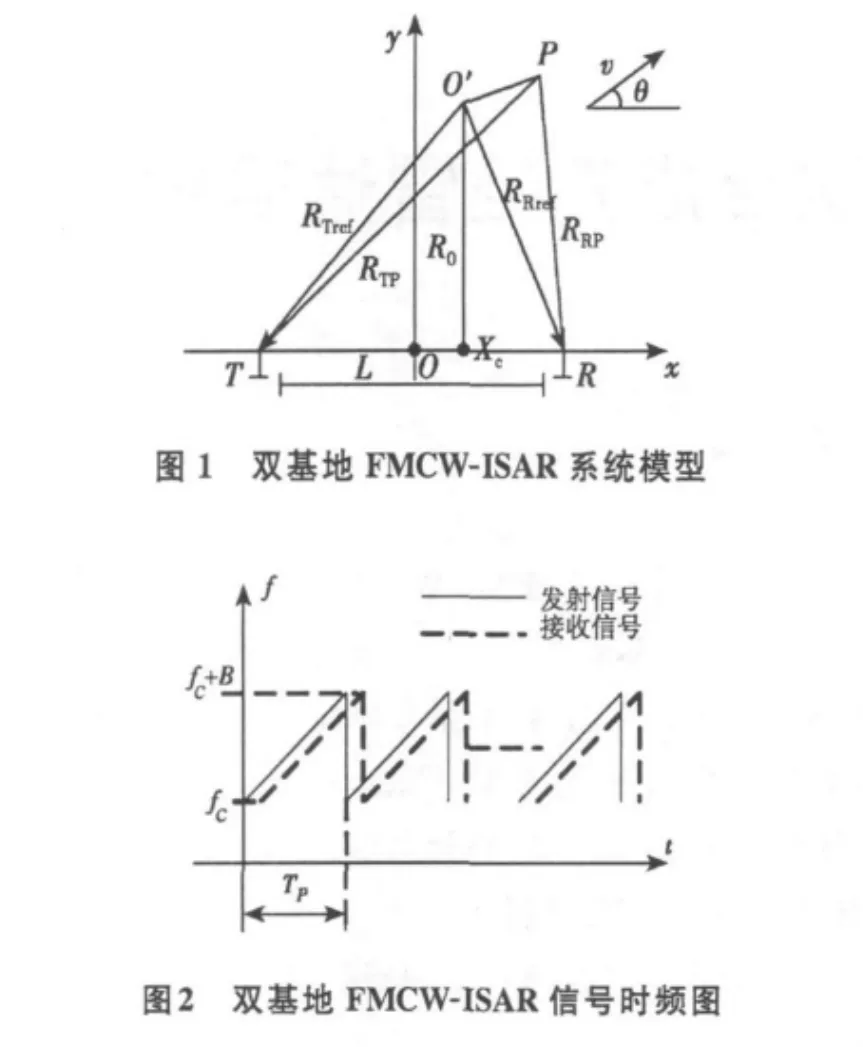
双基地FMCW－ISAR系统采用收发分置的结构特性，且发射机与接收机之间存在严格的时间同步关系，其模型如图1所示。图1中，发射雷达T与接收雷达R的水平基线长度为L，以该水平基线为x轴，基线的中点为坐标原点o建立直角坐标系。o′为目标区域参考点，其初始坐标为（Xc，R0），整个成像过程中，假设发射雷达与接收雷达能够对该点进行精确跟踪，而P为目标点，初始坐标为（Xc＋xP，R0＋yP），以图示速度进行运动。假设发射的FMCW信号为锯齿波，则其发射信号与接收信号的时频关系如图2所示。图中，脉冲宽度为TP，且脉冲重复周期PRI＝TP。

本文中接收雷达工作模式为解线频调工作机制，则接收雷达接收参考点与点目标P的回波信号分别为

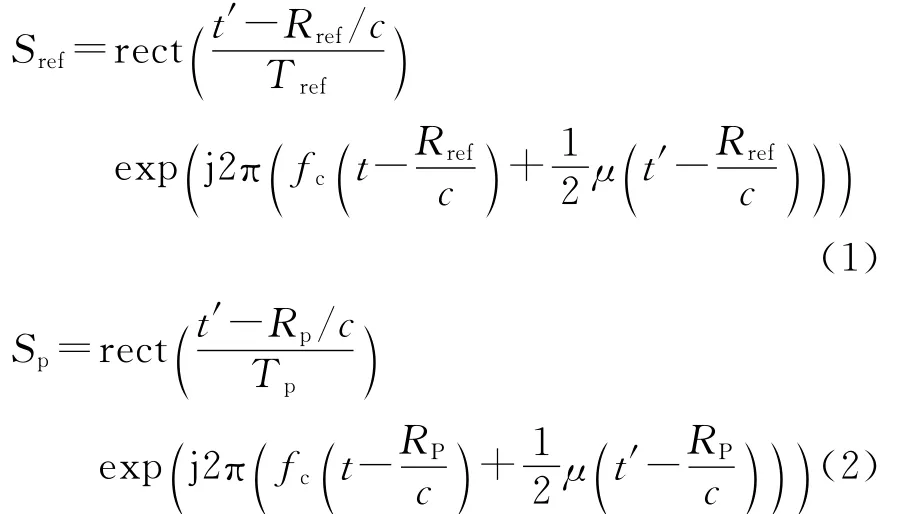
式中：rect（）为矩形窗函数；fc为中心频率；Tp为脉宽；μ为调频率；t′为距离向快时间；t为全时间；Tref为参考信号的脉宽，它比Tp要大一些；Rref和Rp分别为参考点与目标点到收发雷达的距离和，即Rref＝RTref＋RRref，RP＝RTP＋RRP.

双基地接收雷达对FMCW－ISAR回波信号经De－chirp处理后的信号SPref可表示为

3.双基地FMCW－ISAR成像分析

在脉冲式ISAR成像中，基于“走－停”模式的假设，式（3）中的RP是关于慢时间tm的函数，而采用FMCW信号进行ISAR成像时，由于信号的脉冲持续时间较长，脉冲持续时间内由目标运动产生的距离变化不能忽略，因此，在FMCW－ISAR中必须考虑距离快时间t′对瞬时距离和的影响。

3.1 回波信号特性分析

为后续分析方便，将点目标P到双基地雷达的瞬时距离和重新定义为R′P（t′，tm），则根据图1的双基地雷达模型可得

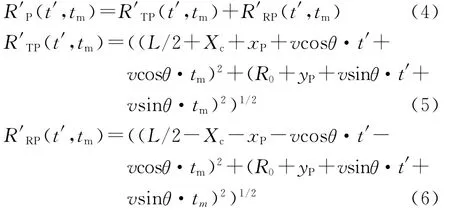
将式（4）在t′＝0处的泰勒级数展开近似为

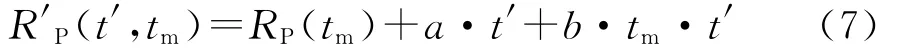
式中：RP（tm）＝RTP（tm）＋RRP（tm），

式（7）的展开式中应用到了两个近似条件，分别是：

1）目标点P相对于参考点o′的相对坐标值xP，yP远小于点P到收发雷达的距离，即xP，yP≪RTP（tm），RRP（tm）；

2）目标点P与参考点到收发雷达的距离相差很小，即式（8）分数变量a，b中的分母部分可用RTref（tm），RRref（tm）代替RTP（tm），RRP（tm）。

假设目标运动速度已知（关于应用FMCW雷达对目标运动参数的估计问题，有兴趣的读者可参阅文献［14］），并结合参考点精确跟踪的假设前提，对单次回波而言，式（8）中a，b是一固定值。

3.2 相位分析与补偿

用式（7）的R′P代替式（3）中的RP，将目标回波信号重写为

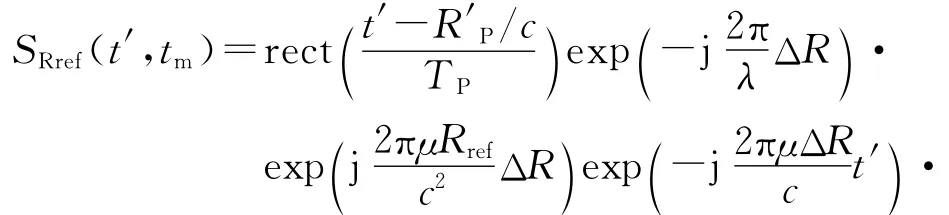
式中：ΔR和Rref是关于慢时间tm的函数，且ΔR＝RP－Rref.

在式（9）中，第一个指数项包含目标的方位多普勒信息，是对目标进行方位向成像的关键；第二个指数项是方位向偏移项，后续分析中会对其进行补偿，暂不考虑其影响；最后一个指数项为采用De－chirp处理特有的剩余视频相位项（RVP），相比脉冲式雷达，FMCW雷达调频率小得多，RVP对成像的影响可以忽略［9］；第三个指数包含目标的距离向信息，是进行距离像分辨的关键；而第四个指数项是距离快时间一次项与慢时间的耦合项，该耦合项造成目标一维距离像的走动；第五个指数项是距离快时间二次项与慢时间的耦合项，该耦合项造成一维距离像主瓣展宽，影响距离像的分辨率，下面重点分析其影响。

从式（9）可以得出双基地FMCW－ISAR回波信号关于快时间t′的相位可以表示为

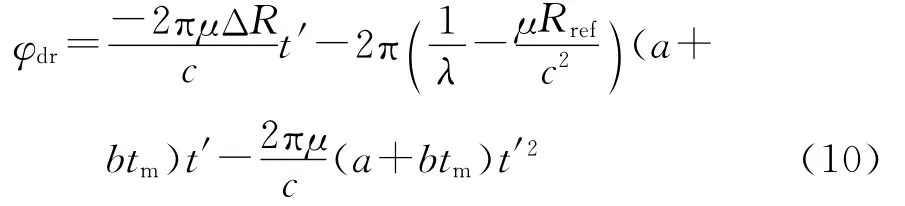
则其距离向多普勒频率可表示成

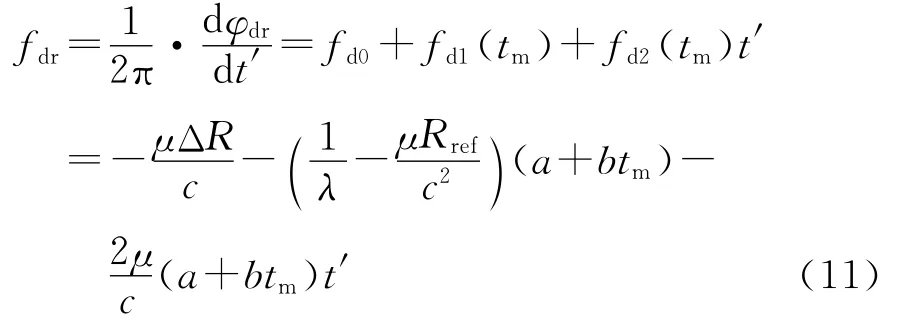
在脉冲式ISAR成像系统中，回波信号在距离频域表现为一单频信号，即式（11）中只有fd0。而对FMCW－ISAR系统而言，回波信号在距离频域表现为起始频率为fd0＋fd1（tm），调频率为fd2（tm）的调频信号形式，同时起始频率中的fd1（tm）和调频率fd2（tm）是关于慢时间tm的时变函数。对单次回波来说，fd1（tm）会导致回波信号在距离多普勒域上产生固定的频偏，而该频偏是随tm变化的，即各次回波在距离多普勒频域上的起始频率不一样，这种随tm变化的频偏造成目标一维距离像谱图表现为一斜线形式，影响后续方位向的相参积累。另一方面，由于调频量fd2（tm）t′的存在，使得回波信号在距离频域不再表现为主瓣宽度很窄的尖峰形式，而是主瓣展宽的类sinc函数形式，主瓣的展宽影响距离向分辨率的下降，导致散焦现象。因此，为聚焦良好的目标二维像必须消除上述距离向的多普勒频偏和调频量的影响。而从上述的分析可以看出，虽然多普勒频偏和调频量是关于慢时间tm的时变函数，但对于单次回波而言，多普勒频偏和调频量是一固定值，因此，可通过对各次回波分别进行补偿来消除快慢时间耦合项对成像质量的影响。

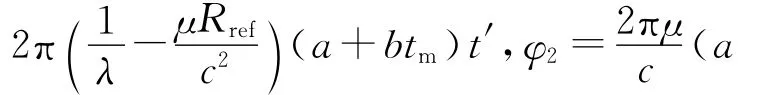
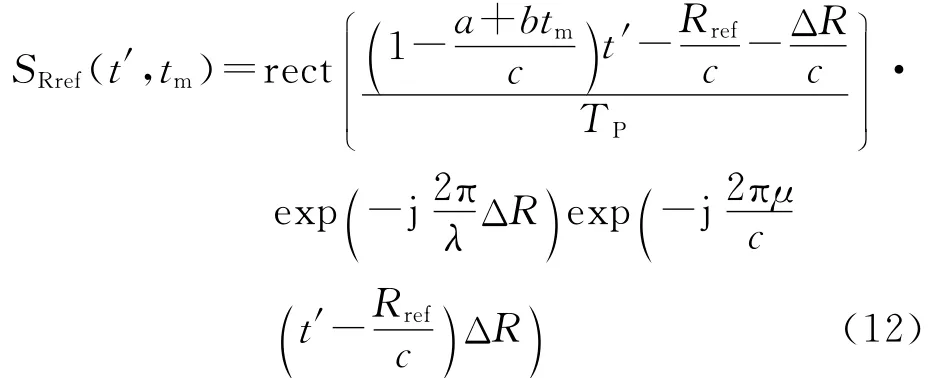
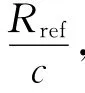
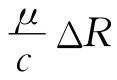
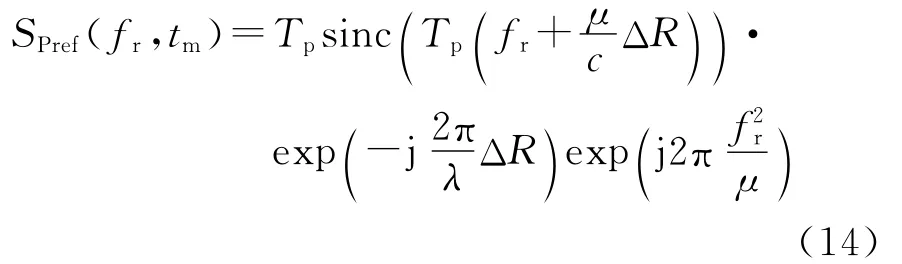
对式（14）补偿掉第二个指数项后便可进行与脉冲式ISAR相类似的方位向相参积累，进而获得目标的二维像。

3.3 成像流程

对双基地FMCW－ISAR系统的回波信号经过上述的距离多普勒域频偏校正和一维距离像主瓣展宽校正后，就可以采用脉冲式ISAR系统的距离－多普勒（RD）算法对目标进行二维成像。其整个成像算法流程如图3所示。

4.仿真验证与分析

为了验证文中所分析问题和所提补偿算法的正确性及有效性，这里对单点目标进行成像仿真。仿真中双基地雷达采用图1所示模型，基线长度L＝100km，参考点o′初始坐标为（Xc，R0）＝（5，50）km，点目标P的初始相对坐标为（xP，yP）＝（3，3）m，且以速度v＝300m／s，与x轴夹角θ＝30度运动；假设雷达发射锯齿波FMCW信号，载频为10 GHz，带宽为300MHz，脉冲持续时间为10ms，整个成像时间为4s.接收雷达配置同发射雷达，采用De－chirp接收方式工作。

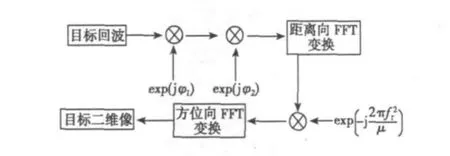
图3 双基地FMCW－ISAR成像流程图

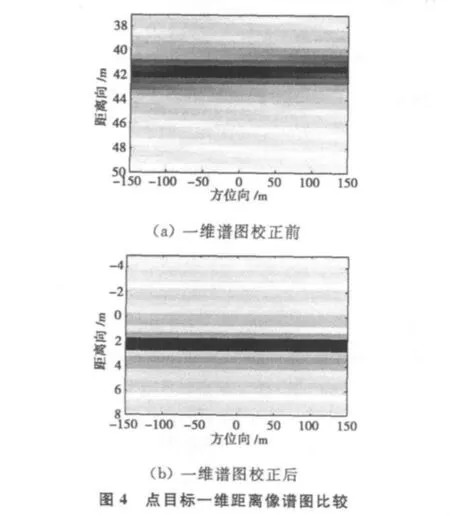
以第256次脉冲为例，由式（11）可得目标一维像的真实坐标ΔR＝－fd0c／μ，虽然单次脉冲内目标走动距离较小，其最大值仅为（a＋btm）·TP≈2.327 m，但根据频偏fd1可得距离偏差的理论计算值为－fd1c／μ≈39.73m.同时图4给出了校正前后点目标一维距离像谱图的比较。为比较清晰方便，在距离向上以宽度为15m的窗取一维距离像放大进行分析。比较图4中的（a）和（b）可以看出，校正前目标的一维距离像谱图中心坐标大约为42.5m，而校正后谱图中心坐标约为2.5m，仿真结果与理论分析相吻合。随着方位向距离的变化，谱图中心也在变化，整个谱图呈现斜线形式，这和上述固定频偏随慢时间变化的分析相吻合；同时，由于调频量的影响，谱图在距离向上存在明显的展宽现象，影响距离像的高分辨。通过文中的算法补偿后，点目标一维距离像谱图由斜线校正成直线，有利于方位向的相参积累，距离展宽现象也得到明显改善，提高了距离向的分辨率。

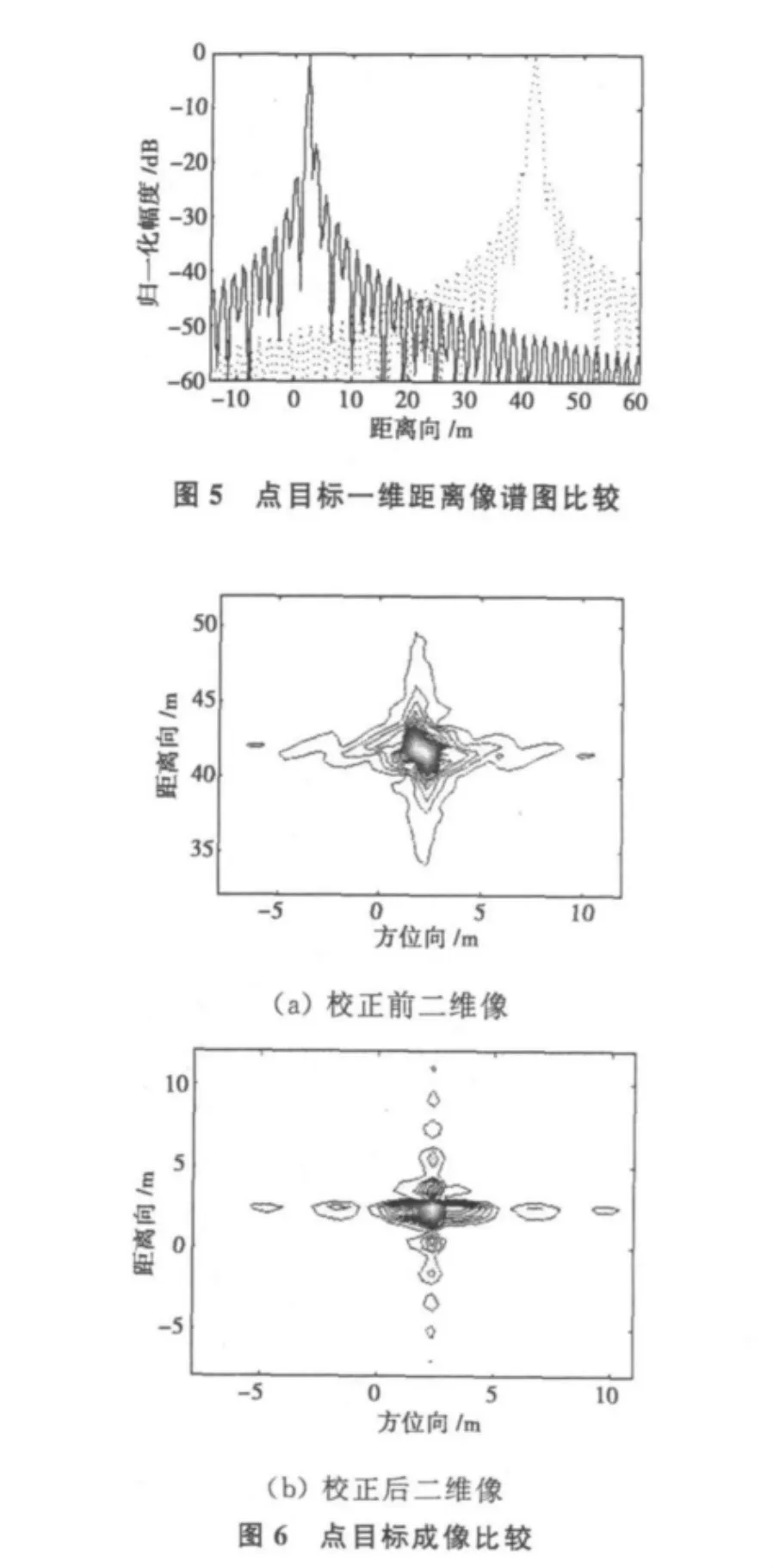
为了更直观地说明问题，文中给出了校正前后一维距离像剖面图和点目标成像比较图，如图5和图6所示。从图5可以看出，校正后一维距离像主瓣明显变窄，消除了由调频量引起的主瓣展宽现象。由于文中的补偿算法采用逐次回波校正的方式，在校正随慢时间变化的多普勒频偏和调频量的同时也消除了快时间对方位聚焦的影响。因此，本文的校正算法有利于距离向和方位向的同时聚焦，校正前后点目标成像比较见图6。

5.结 论

本文将FMCW雷达和双基地ISAR成像系统相结合，通过对回波信号的分析得知：采用FMCW信号进行双基ISAR成像时，由脉冲持续时间较长导致的距离快时间和方位慢时间耦合会造成目标一维距离像产生频偏和主瓣展宽现象。针对该问题，文中提出采用逐次回波补偿的方法消除快慢时间耦合对目标成像质量的影响并取得了较好的结果。

［1］EDRICH M.Ultra－lightweight synthetic aperture radar based on a 35GHz FMCW sensor concept and online raw data transmission［J］.IEE Proc－Radar Sonar Naving，2006，153（2）：129－134.

［2］EDRICH M，WEISS G.Second－Generation Ka－Band UAV SAR System［C］／／Prcc－38th Euro Micro Con..Amsterdam，2008：1636－1639.

［3］熊俊志，杨子杰，周辉林.非连续谱FMCW雷达信号分析与处理［J］.电波科学学报，2006，21（3）：377－381.

XIONG Junzhi，YANG Zijie，ZHOU Huilin.Signal analysis and processing for discontinuous spectra FMCW radar［J］.Chinese Journal of Radio Science，2006，21（3）：377－381.（in Chinese）

［4］梁 毅，井 伟，邢孟道，等.一种下视三维FMCW SAR成像的新方法［J］.自然科学进展，2009，19（5）：575－584.

LIANG Yi，JING Wei，XING Mengdao，et al.A new method of down－looking three dimension FMCW－SAR imaging［J］.Natural Science Progress，2009，19（5）：575－584.（in Chinese）

［5］杨明磊，陈伯孝，张守红，等.多载频FMCW在MIMO雷达中的应用研究［J］.电子学报，2008，36（12）：2351－2356.

YANG Minglei，CHEN Boxiao，ZHANG Shouhong，et al.Study on application of multiple carrier frequency FMCW in MIMO radar［J］.Acta Electronica Sinica，2008，36（12）：2351－2356.（in Chinese）

［6］WANG R，LOFFELD O，NIES H，et al.Focus FMCE SAR data using the wavenumber domain algorithm［J］.IEEE Trans on Geo－Rem sensing，2010，48（4）：2109－2118.

［7］董勇伟，梁兴东，丁赤飚.调频连续波SAR非线性处理方法研究［J］.电子与信息学报，2010，32（5）：1034－1039.

DONG Yongwei，LIANG Xingdong，DING Chibiao.Non－liner signal processing for FMCW SAR［J］.Journal of Electronics ＆Information Technology，2010，32（5）：1034－1039.（in Chinese）

［8］杜 雨，杨建宇.线性FMCW雷达动目标一维距离像运动补偿［J］.电波科学学报，2006，21（1）：104－108.

DU Yu，YANG Jianyu.Motion compensation of 1－D range profile for linear FMCW radar［J］.Chinese Journal of Radio Science，2006，21（1）：104－108.（in Chinese）

［9］杜 雨，杨建宇.基于FRFT的LFMCW雷达加速动目标检测与参数估计［J］.电波科学学报，2005，20（6）：815－819.

DU Yu，YANG Jianyu.Novel method of moving target detection and parameter estimation for LFMCW radar［J］.Chinese Journal of Radio Science，2005，20（6）：815－819.（in Chinese）

［10］META A，HOOGEBOOM P，LIGTHART L P.Signal processing fof FMCW SAR［J］.IEEE Trans on Geos ＆ Remote Sensing，2007，45（11）：3519－3532.

［11］张大炜，魏 芳，王岩飞.多普勒效应对FMCWSAR系统成像性能的影响分析［J］.电子与信息学报，2008，30（3）：559－563.

ZHANG Dawei，WEI Fang，WANG Yanfei.Analysis of the doppler effect in FMCW－SAR and its influence on the image of the system［J］.Journal of Electronics ＆ Information Technology，2008，30（3）：559－563.（in Chinese）

［12］王 颖，曲长文，平殿发，等.二次相位误差对FMCW－SAR成像质量的影响［J］.指挥控制与仿真，2009，31（1）：104－106.

WANG Ying，QU Changwen，PING Dianfa，et al.Influence of Secondary Phase Error to Image Quality for FMCW－SAR［J］.Command Control ＆ Simulation，2009，31（1）：104－106.（in Chinese）

［13］GIUSTI E，MARTORELLA M.Range doppler and image auto focusing for FMCW inverse synthetic aperture radar［C］／／Radar Conference－Surveillance for a Safer World，Bordeaux，2009：1－6.

［14］秦国栋，陈伯孝，杨明磊，等.双基地多载频FMCW雷达目标加速度和速度估计方法［J］.电子与信息学报，2009，31（4）：794－797.

QIN Guodong，CHEN Baixiao，YANG Minglei，et al.Acceleration and velocity estimation of targets in bi－static multi－frequency FMCW radar［J］.Journal of Electronics ＆ Information Technology，2009，31（4）：794－797.（in Chinese）