双腔室自激振荡喷嘴频率特性研究

2011-06-02裴江红唐川林

振动与冲击 2011年4期

裴江红，唐川林，胡东

(湖南工业大学水射流研究所，湖南株洲 412008)

自激振荡脉冲射流是一种利用流体自激振荡机理发展起来的一种新型高效脉冲射流。较其它脉冲射流而言它具有结构简单、无激振源，无运动件的密封特点，而被广泛应用于清洗、破岩、建筑、切割和辅助采矿等行业［1－3］。自激振荡机理是当射流或剪切流在在剪切层向下游流动过程中，由于剪切层的不稳定性对涡量具有选择放大的作用，致使射流中能满足放大条件的一定频率的涡流得到放大，并形成一连串离散的涡环，当其与下游碰撞壁发生相互作用时，在碰撞区周围形成压力扰动波并以声速的方式向上游传播，诱发新的涡量扰动重复以上过程，从而导致碰撞区周围剪切层大幅度横向波动，当其波及到射流核心层时使得腔室出口处流体阻抗出现周期的变化形成调制射流，形成自激振荡脉冲射流［4－7］。国内外学者实验表明，自激振荡脉冲射流峰值压力较连续射流可以提高15%～20%。如何进一步提高脉冲射流峰值压力，成为众多学者研究的热点，但目前还主要集中在通过对单腔室自激振荡腔结构尺寸和上、下喷嘴孔径的优化来获得最佳的谐振效果，从而达到提高脉冲射流峰值压力［2，6］。本文拟对双腔室自激振荡喷嘴这一新型喷嘴作一个有益的探索，以期从理论上探讨双腔室自激振荡喷嘴是否能获得比单腔室喷自激振荡喷嘴更高的峰值压力，以期能为今后的工程实践服务，其结构模型图如图1所示。根据相似性理论从产生自激振荡脉冲射流的结构系统出发，分析双腔室自激振荡脉冲装置结构参数对射流峰值、喷嘴固有频率的影响。

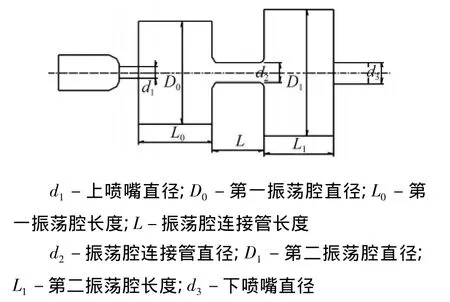
图1 双腔室自激振荡喷嘴模型Fig.1 the model of double chambers self-excited oscillation pulsed water jet nozzle

1 双腔室自激振荡喷嘴模型建立

根据流体神经网络理论［8］，可以用集中元件的方法来简化谐振腔中的振荡。以流体质量流量比拟电流，以流体压力比拟电压，以流阻比拟电阻，由相似性建立双腔室自激振荡脉冲射流喷嘴的集中参数网络模型(如图2)所示。其中R1、R2分别为上、中、下喷嘴的流阻;L为喷嘴前管路流感;C1、C2分别为一振荡腔、二振荡腔流容，。根据流体网络的似稳假定，对小扰动信号其紊流流阻是非线性的，动态电阻为:

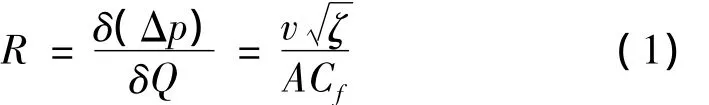
式中:v－流体平均速度，单位m/s;ζ－喷嘴局部阻力系数;A－喷嘴截面面积，单位m2;Cf－喷嘴流量系数。

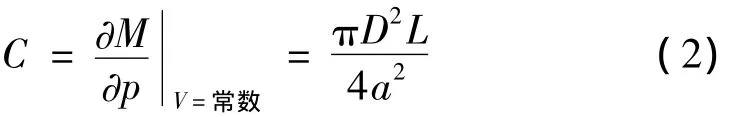
式中:D－振荡腔直径，单位m;L－振荡腔长度，单位m;a－振荡腔内流体的波速，单位m/s。

式中:l0－上喷嘴前管路长度，单位m;d0－上喷嘴前管路直径，单位m。

图2 双腔室自激振荡喷嘴集中参数网络模型Fig.2 Lumped parameter net model of double chambers self-excited oscillation pulsed water jet nozzle

根据电气网络理论，对双腔室喷嘴参数网络模型分析如下:

系统中元件L、C2和R2所组成的阻抗:

整个系统的总阻抗:

经过R2所产生的压降:

将上式整理后得:

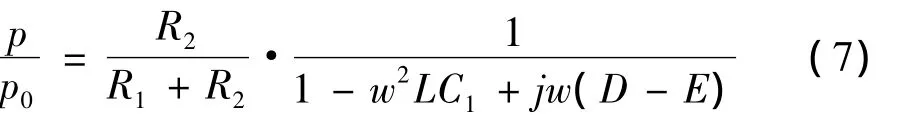
式中:

系统相应的频率响应函数、幅频特性和相频特性分别为:

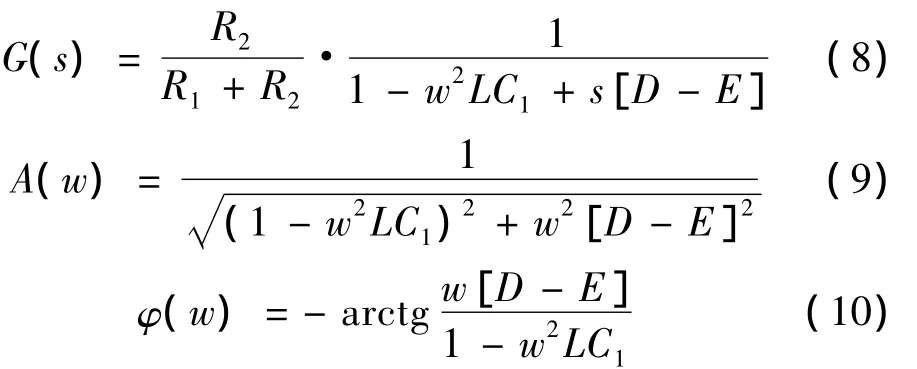
系统发生自激振荡的条件是方程(7)中虚部为零即:

由方程(8)可求得系统固有频率:

2 计算结果与分析

在串联式自激振荡脉冲喷嘴的设计过程中，参考了单腔室自激振荡脉冲喷嘴设计中的有关经验［1，5］。取上游喷嘴为流线型喷嘴，下游喷嘴为圆孔喷嘴。取上喷嘴入口处初始压力10 MPa，d1=2 mm，d2/d1=1.2，d3/d2=1.2，D0/d1=20，D1/d2=20，l/d2=10。将以上数值代入到由双腔室喷嘴参数网络模型所确定的方程(1)、(2)、(3)、(9)和(10)，利用 Matlab 软件编程计算可得到在不同腔长、不同腔径下系统的幅频，相频特性(见图3，图4)。在计算系统的幅频特性时，取喷嘴内流体内的波速a=500 m/s，主要是考虑到射流在自激振荡腔内不可避免的会产生空化现象，在中心射流区周围形成近周期性移动且大小变化的汽囊环，这些汽囊环的出现不可避免的会降低喷嘴内流体的波速。图3可见:双腔室自激振荡脉冲射流喷嘴具有很好的低通滤波功能和较好的增压特性。喷嘴系统存在一个低通频带，当喷嘴内射流频率位于低通频带内时将产生增压效果，这表明我们在设计喷嘴系统时应使喷嘴系统的低通频带包含来流的主频带并使喷嘴的固有频率接近来流脉动主频，因此只有在了解喷嘴结构参数与固有频率规律的前提下才能设计出合理的喷嘴。

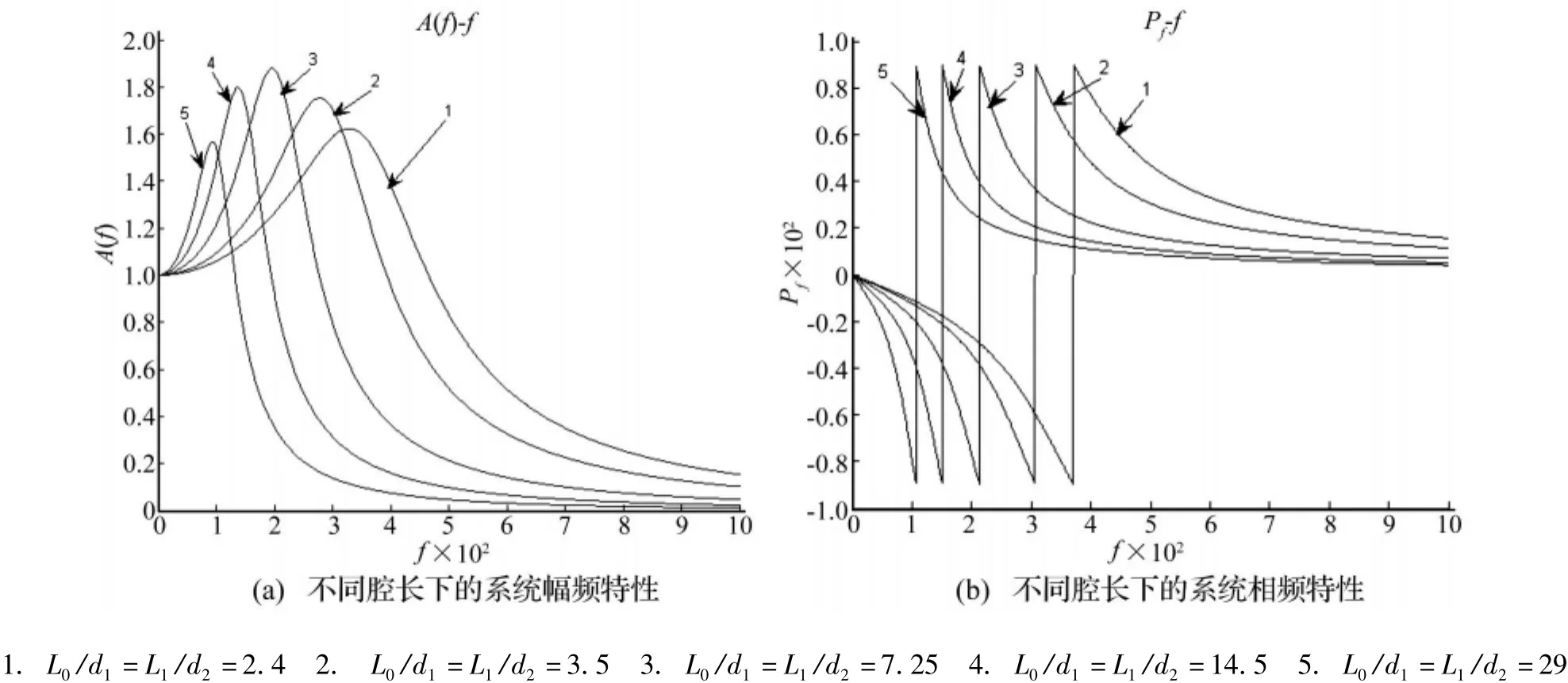
图3 不同腔长下的系统频率特性Fig.3 the frequency characters on different chamber length

图4 不同腔径下的频率特性Fig.4 the frequency characters on different chamber diameter

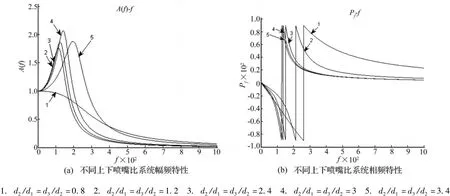
图5 不同上下喷嘴比系统频率特性Fig.5 The frequency character on the different diameter ratio of nozzle

由图3可知，当喷嘴的振荡腔长度发生变化时，系统的幅值随着振荡腔长度的增加先升高而后减小，存在一个极值对应的腔长(L0/d1=7.25，L1/d2=7.25)，这与单腔室自激振荡喷嘴系统最大谐振峰值对应的最佳腔长(L/d=2.4)［1，3，6］有显著的不同。本系统最佳腔长对应的幅值为 1.878，峰值压力提高达到了87.8%，这充分表明双腔室自激振荡喷嘴较单腔室自激振荡喷嘴具有更好的增压效果;系统的谐振频率随着腔长的增加而减小，本系统最大谐振峰值对应的固有频率为196 Hz远小于参考文献［5］中单腔室喷嘴最大谐振峰值所对应的固有频率584 Hz。分析其原因在于:根据双腔室喷嘴参数网络模型知，第一振荡腔室与第二振荡腔室所产生的阻抗为一并联关系，从而导致整个系统的总阻抗小于单个腔室所产生的阻抗，从而出现了双腔室谐振频度低于单腔室谐振频率。系统的腔长发生变化时表现出了相似的相频特性规律:随着频率的增加，相位滞后角度越来越大，当达到其谐振频率时，相位发生一个阶跃增加使相位达到最大超前角度，随之随频率的增加相位超前角度逐渐减小。这主要是由于当频率较小时系统阻抗呈流容性阻抗性，系统出现了相位滞后;当频率达到一定值时，系统阻抗又要表现了流感性阻抗，系统产生了相位超前，故在系统相频特性图中呈现出了相位阶跃变化现象。阶跃变化时对应的频率即为固有频率。

由图4可见，振荡腔直径对系统幅频特性影响也较大，系统固有频率随振荡腔直径的增大而减小，系统的低通频带随振荡腔直径的增大而变窄，存在与最大幅值对应的腔径比(D0/d1=20，D1/d2=20)(这与文献中提到的在单腔室下，最大幅值对应的腔径比相同)，总的来说振荡腔直径对系统幅频特性影响规律与腔长对系统幅频特性影响规律类似。这主要是因为振荡腔直径与振荡腔长度变化对系统中流容的影响规律相似造成的。

图5表明，系统的固有频率随上下喷嘴比值的增大而逐渐减小，系统的通频带随上下喷嘴比值的增大先增大而后减小，系统的最大峰值对应最优上下喷嘴直径比(d2/d1=d3/d2=3)。此值远高于单腔室自激振荡脉冲喷嘴的最佳上下喷嘴直径比1.2。